Toán 6 Bài tập cuối chương 1 - Chân trời sáng tạo Giải Toán lớp 6 trang 45, 46, 47 - Tập 1

Giải Toán lớp 6 Bài tập cuối chương 1 bao gồm đáp án chi tiết, cùng hướng dẫn giải các bài tập trong SGK Toán 6 Tập 1 Chân trời sáng tạo trang 45, 46, 47.

Lời giải Toán 6 Chân trời sáng tạo trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 6, từ đó học tốt môn Toán lớp 6 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài tập cuối chương I - Số tự nhiên. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 6 Chân trời sáng tạo phần Trắc nghiệm trang 45, 46 tập 1

Câu 1

Gọi X là tập hợp các chữ cái trong “từ thanh”. Cách viết đúng là:

(A) X = {t; h; a; n; h}.

(B) X = {t; h; n};

(C) X= {t; h; a; n}.

(D) X = {t; h; a; n; m}.

Lời giải chi tiết:

Khi liệt kê các phần tử ta chỉ liệt kê phần tử đó duy nhất 1 lần:

Tập hợp các chữ cái trong từ “thanh” là: X = {t; h; a; n}

Câu 2

Gọi X là tập hợp các số tự nhiên không lớn hơn 5. Cách viết sai là:

(A) X = {0; 1; 2; 3; 4; 5}.

(B) X = {0; 2; 4; 1; 3; 5}.

(C) X= {x ∈ N | x < 5}.

(D) X = {x ∈ N | x ≤ 5}.

Lời giải chi tiết:

X là tập hợp các số tự nhiên không lớn hơn 5.

X là: 0; 1; 2; 3; 4; 5

⇒ X = {0; 1; 2; 3; 4; 5}

Câu 3

Cách viết nào sao đây là sai:

(A) a + b = b + a.

(B) ab = ba.

(C) ab + ac = a(b + c).

(D) ab - ac = a(c - b).

Lời giải chi tiết:

(A) a + b = b + a ⇒ Tính chất giao hoán của phép cộng

(B) ab = ba ⇒ Tính chất giao hoán của phép nhân

(C) ab + ac = a(b + c) ⇒ Tính chất phân phối của phép nhân đối với phép cộng.

(D) ab - ac = a(c - b)

Ta có: ab – ac = a(b – c) Tính chất phân phối của phép nhân đối với phép trừ.

a(b – c) ≠ a(c – b)

Câu 4

Nhẩm xem kết quả phép tính nào dưới đây là đúng:

(A) 11 . 12 = 122.

(B) 13 . 99 = 1170.

(C) 14 . 99 = 1386.

(D) 45 . 9 = 415.

Lời giải chi tiết:

Phương pháp nhẩm tách số: Đưa một hay nhiều số hạng về dạng tròn chục hoặc tròn trăm, tròn nghìn, …

Ví dụ: 99 = 100 - 1

(A) 12 . 11 = 12 . (10 – 1) = 12 . 10 – 12 . 1 = 120 – 12 = 108 ≠ 122

(B) 13 . 99 = 13 . (100 – 1) = 13 . 100 – 13 . 1 = 1 300 – 13 = 1 287 ≠ 1 170

(C) 14 . 99 = 14 . (100 – 1) = 14 . 100 – 14 . 1 = 1400 – 14 = 1 386

(D) 45 . 9 = 45 . (10 – 1) = 45 . 10 – 45 . 1 = 450 – 45 = 405 ≠ 415

Câu 5

ƯCLN(18, 24) là:

(A) 24

(B) 18

(C) 12

(D) 6

Lời giải chi tiết:

Ta có:

Câu 6

BCNN(3, 4, 6) là:

(A) 72

(B) 36

(C) 12

(D) 6

Lời giải chi tiết:

 Ta có:

Giải Toán 6 Chân trời sáng tạo phần Tự luận trang 46, 47 tập 1

Bài 1

Tính giá trị của biểu thức (bằng cách hợp lí nếu có thể):

a) A = 37 . 173 + 62 . 173 + 173;

b) B = 72 . 99 + 28 . 99 – 900;

c) C = 2³ . 3 – (1¹⁰ + 15) : 4²;

d) D = 6² : 4 . 3 + 2 . 5² - 210⁰.

Hướng dẫn giải

- Tính chất phân phối của phép cộng đối với phép nhân: a.(b + c) = a.b + a.c

- Với các biểu thức không có dấu ngoặc ta tính theo thứ tự như sau:

Lũy thừa ➙ nhân và chia ➙ cộng và trừ

- Với các biểu thức có dấu ngoặc ta tính theo thứ tự như sau:

( ) ➙ [ ] ➙ { }

Gợi ý đáp án:

Bài 2

Tìm các chữ số x, y biết:

a)  chia hết cho 2; 3 và cả 5.

b)  chia hết cho 5 và 9 mà không chia hết cho 2.

Hướng dẫn giải

- Dấu hiệu chia hết cho 2: Số có chữ số tận cùng là 0; 2; 4; 6; 8

- Dấu hiệu chia hết cho 5: Số có chữ số tận cùng là 0; 5

- Dấu hiệu chia hết cho 3: Tổng các chữ số của số đó chia hết cho 3 thì chia hết cho 3.

- Dấu hiệu chia hết cho 9: Tổng các chữ số của số đó chia hết cho 9 thì chia hết cho 9.

Gợi ý đáp án:

a)   chia hết cho 2 và 5 khi chữ số tận cùng của nó là 0

=> y = 0

chia hết cho 3 khi tổng các chữ số của nó cũng chia hết cho 3

Nên 1 + 2 + x + 0 + 2 + 0 ⋮ 3

=> x + 5 ⋮ 3 và 0 ≤ x ≤ 9

=> x ∈ {1; 4; 7}

Vậy để  chia hết cho 2; 3 và cả 5 thì y = 0 và x ∈ {1; 4; 7}.

b)  chia hết cho 5 mà không chia hết cho 2 khi chữ số tận cùng của nó là 5

=> y = 5

chia hết cho 9 khi tổng các chữ số của nó cũng chia hết cho 9

Nên 4 + 1 + 3 + x + 2 + 5 ⋮ 3

=> x + 15 ⋮ 9 và 0 ≤ x ≤ 9

=> x = 3

Vậy để chia hết cho 5 và 9 mà không chia hết cho 2 thì y = 5 và x = 3.

Bài 3

Viết các tập hợp sau bằng cách liệt kê các phần tử:

a) A = {a ∈ N | 84 ⋮ a và a > 6}.

b) B = {b ∈ N | b ⋮ 12, b ⋮ 15, b ⋮ 18 và 0 < b < 300}.

Hướng dẫn giải

Chú ý: Khi liệt kê các phần tử chỉ được liệt kê duy nhất một lần.

Áp dụng cách tìm BCNN, UCLN của hai hay nhiều số tự nhiên.

Gợi ý đáp án:

a) Theo đề bài: 84 chia hết cho a và 180 chia hết cho a nên a ∈ ƯC(84, 180) và a > 6.

Ta có: 84 = 2² . 3 . 7

180 = 2² . 3² . 5

ƯCLN(84, 180) = 2² . 3

=> a ∈ ƯC(84, 180) = Ư(12) = {1; 2; 3; 4; 6; 12}

Mà a > 6.

=> a = 12

* Vậy tập hợp A = {12}.

b) Vì b chia hết cho 12, b chia hết cho 15, b chia hết cho 18 nên b ∈ BC(12, 15, 18) và 0 < b < 300

Ta có: 12 = 2² . 3

15 = 3 . 5

18 = 2 . 3²

=> BCNN(12, 15, 18) = 2² . 3² . 5 = 180

=> b ∈ BC(12, 15, 18) = B(180) = {0; 180; 360;…}

Mà 0 < b < 300

=> b = 180

* Vậy tập hợp B = {180}.

Bài 4

Trong dịp "Hội xuân 2020", để gây quỹ giúp đỡ các bạn học sinh có hoàn cảnh khó khăn, lớp 6A bán hai mặt hàng (như bảng ở cột bên) với mục tiêu số tiền lãi thu được là 500 000 đồng.

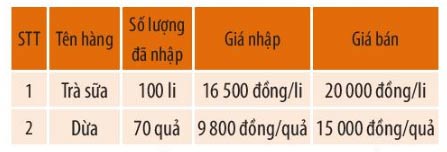
Trong thực tế các bạn đã bán được số lượng hàng như sau: trà sữa bán được 93 li, dừa bán được 64 quả.

Hỏi lớp 6A đã thu được bao nhiêu tiền lãi? Lớp 6A có hoàn thành mục tiêu đã đề ra không?

Hướng dẫn giải

Tiền lãi = Tiền thu được – Tiền vốn mua hàng

Gợi ý đáp án:

Số tiền lớp 6A bỏ ra để nhập hàng là:

100 . 16 500 + 70 . 9 800 = 2 336 000 (đồng)

Số tiền lớp 6A bán được là:

93 . 20 000 + 64 . 15 000 = 2 820 000 (đồng)

Số tiền lãi lớp 6A thu được là:

2 820 000 - 2 336 000 = 484 000 (đồng) < 500 000 (đồng)

Vậy: Với mục tiêu số tiền lãi thu được là 500 000 đồng thì lớp 6A không hoàn thành mục tiêu đã đề ra.

Bài 5

Thực vật được cấu tạo bởi các tế bào. Tế bào lớn lên đến một kích thước nhất định thì phân chia ra thành 2 tế bào con. Các tế bào con tiếp tục tăng kích thước và lại phân chia thành 4 tế bào, rồi thành 8 tế bào, ...

Hãy cho biết số tế bào con có được sau lần phân chia thứ tư, thứ năm, thứ sáu từ một tế bào ban đầu.

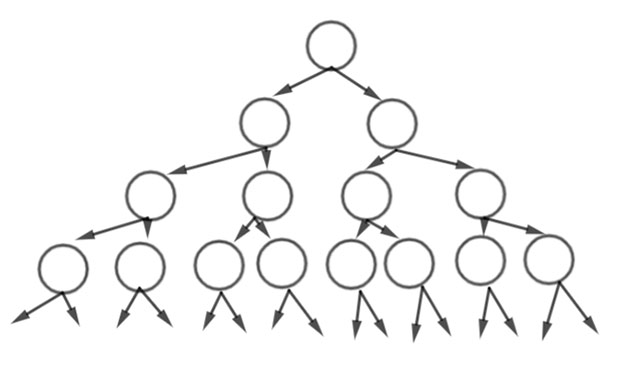
Gợi ý đáp án:

• Lần 1: Phân chia thành 2 tế bào con
• Lần 2: Phân chia thành 4 tế bào con => 4 = 2²
• Lần 3: Phân chia thành 8 tế bào con => 8 = 2³

=> Ta nhận thấy các tế bào phân chia theo lũy thừa của cơ số 2.

Vậy:

• Số tế bào con có được sau lần phân chia thứ tư là: 2⁴ = 16 tế bào
• Số tế bào con có được sau lần phân chia thứ năm là: 2⁵ = 32 tế bào
• Số tế bào con có được sau lần phân chia thứ sáu là: 2⁶ = 64 tế bào.

Bài 6

Huy chơi trò xếp 36 que tăm thành những hình giống nhau như các hình dưới đây. Trong mỗi trường hợp a, b, c, d, Huy xếp được bao nhiêu hình như vậy?

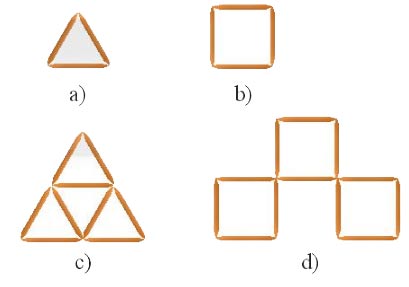
Hướng dẫn giải

Thực hiện phép chia 36 cho số que tạo nên từng hình.

a = b . q + r

Gợi ý đáp án:

a) Ở trường hợp a, Huy dùng 3 que tăm để xếp được 1 hình.

Vậy với 36 que tăm thì Huy xếp được số hình là: 36 : 3 = 12 hình.

b) Ở trường hợp b, Huy dùng 3 que tăm để xếp được 1 hình.

Vậy với 36 que tăm thì Huy xếp được số hình là: 36 : 4 = 9 hình.

c) Ở trường hợp c, Huy dùng 9 que tăm để xếp được 1 hình.

Vậy với 36 que tăm thì Huy xếp được số hình là: 36 : 9 = 4 hình.

d) Ở trường hợp d, Huy dùng 12 que tăm để xếp được 1 hình.

Vậy với 36 que tăm thì Huy xếp được số hình là: 36 : 12 = 3 hình.

Bài 7

a) Hoàn thiện bảng sau vào vở.

b) Nhận xét về tích

ƯCLN(a, b) . BCNN(a, b) và tích a . b.

Hướng dẫn giải

- Muốn tìm ƯCLN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung.

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó.

Tích đó là ƯCLN phải tìm.

- Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó.

Tích đó là BCNN phải tìm.

Gợi ý đáp án:

a)

b) Nhận xét: Nhìn vào bảng trên ta thấy tích ƯCLN(a, b) . BCNN(a, b) bằng với tích a . b.

Bài 8

Nhóm các ban lớp 6B cần chia 48 quyển vở, 32 chiếc thước kẻ và 56 chiếc bút chì vào trong các túi quà để mang tặng các bạn ở trung tâm trẻ mồ côi sao cho số quyển vở, thước kẻ và bút chì ở mỗi túi đều như nhau. Tính số lượng túi quà nhiều nhất mà nhóm các bạn có thể chia được. Khi đó, số lượng vở, thước kẻ, bút chì trong mỗi túi là bao nhiêu?

Hướng dẫn giải

- Muốn tìm UCLN của hai hay nhiều hơn 1 số ta thực hiện ba bước sau:

Bước 1: Phân tích mỗi số ra thừa số nguyên tố

Bước 2: Chọn ra các thừa số nguyên tố chung

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó.

Tích đó là UCLN phải tìm.

Gợi ý đáp án:

Vì lớp 6B chia túi quà có số quyển vở, thước kẻ bút chì ở mỗi túi đều nhau nên nên ta phải tìm UCLN(48; 32; 56)

Ta có:

Vậy số lượng túi quả nhiều nhất mà nhóm các bạn có thể chia được là 8 túi

Mỗi túi có số quyển vở là: 48 : 8 = 6 (quyển)

Mỗi túi có số thước kẻ là: 32 : 8 = 4 (chiếc)

Mỗi túi có số bút chỉ là: 56 : 8 = 7 (chiếc)

Bài 9

TOÁN VÀ THƠ

Trung thu gió mát trăng trong
Phố phường đông đúc, đèn lồng sao sa
Rủ nhau đi đếm đèn hoa
Quẩn quanh, quanh quẩn biết là ai hay
Kết năm, chẵn số đèn này
Bảy đèn kết lại còn hai ngọn thừa
Chín đèn thời bốn ngọn dư
Đèn hoa bao ngọn mà ngơ ngẩn lòng.

(Cho biết số đèn từ 600 đến 700 chiếc).

Hướng dẫn giải

Dấu hiệu chia hết cho 5: Chữ số tận cùng của số đó là 0 hoặc 5

a = b.q + r

BCNN(a; b) = c ⇒ BC(a; b) = B(c)

Gợi ý đáp án:

Gọi x là số chiếc đèn hoa (600 ≤ x ≤ 700)

“Kết năm, chẵn số đèn này” ⇒ x chia hết cho 5

Đặt x = 5a ⇒ x + 5 = 5a + 5 chia hết cho 5

“Bảy đèn kết lại còn hai ngọn thừa” ⇒ x chia 7 dư 2

Đặt x = 7m + 2 ⇒ x + 5 = 7m + 2 + 5 = 7m + 7 chia hết cho 7

“Chín đèn thời bốn ngọn dư” ⇒ x chia 9 dư 4

Đặt x = 9n + 4 ⇒ x + 5 = 9n + 4 + 5 = 9n + 9 chia hết cho 9

⇒ x + 5 chia hết cho cả 2 số 5; 7; 9

Hay x + 5 = BC(5; 7; 9)

Do 5, 7; 9 là các số đôi một nguyên tố cùng nhau nên BCNN(5; 7; 9) = 5.7.9 = 315

⇒ BC(5, 7; 9) = B(315) = {0; 315; 630; 945; ….}

Do 600 ≤ x ≤ 700 nên x + 5 = 630 ⇒ x = 630 – 5 = 625

Vậy số đèn hoa là 625 chiếc.