Toán 6 Bài 5: Phép nhân và phép chia phân số Giải Toán lớp 6 trang 20 sách Chân trời sáng tạo - Tập 2

Bài trước

Mục lục

Bài sau

Giải Toán lớp 6 bài 5: Phép nhân và phép chia phân số hướng dẫn rất chi tiết các bước giải các bài tập trong SGK Toán 6 Tập 2 Chân trời sáng tạo trang 19, 20. Đồng thời, còn tổng hợp cả lý thuyết trọng tâm, cùng những dạng bài tập trắc nghiệm cho các em ôn tập thật tốt.

Với lời giải Toán 6 Bài 5 rất chi tiết, được biên soạn kỹ lưỡng, còn giúp thầy cô tham khảo để soạn giáo án Bài 5: Phép nhân và phép chia phân số - Chương 5: Phân số cho học sinh của mình. Vậy mời thầy cô và các em cùng tham khảo bài viết dưới đây của Download.vn:

Giải Toán 6 bài 5: Phép nhân và phép chia phân số

Giải Toán 6 Chân trời sáng tạo Hoạt động
Giải Toán 6 Chân trời sáng tạo Thực hành
Giải Toán 6 Chân trời sáng tạo trang 20 tập 2
Lý thuyết phép nhân và phép chia phân số
Trắc nghiệm Toán 6 Bài 5: Phép nhân và phép chia phân số

Giải Toán 6 Chân trời sáng tạo Hoạt động

Hoạt động 1

Độ cao của đáy vịnh Cam Ranh là −32 m. Độ cao của đáy sông Sài Gòn bằng $\frac{5}{8}$ $\frac{5}{8}$ độ cao của đáy vịnh Cam Ranh. Hỏi độ cao của đáy sông Sài Gòn là bao nhiêu mét?

Gợi ý đáp án:

Ta có:

Độ cao của đáy sông Sài Gòn bằng $\frac{5}{8}$ $\frac{5}{8}$ độ cao của đáy vịnh Cam Ranh

Nghĩa là:

Độ cao của đáy sông Sài Gòn chiếm 5 phần và độ cao của đáy vịnh Cam Ranh chiếm 8 phần.

Khi đó, giá trị của một phần là: (−32) : 8 = −4 (m)

Độ cao của đáy sông Sài Gòn là: (−4) . 5 = −20 (m)

Vậy độ cao của đáy sông Sài Gòn là −20 m

Hoạt động 2

Một hình chữ nhật có diện tích $\frac{{48}}{{35}}{m^2}$ $\frac{{48}}{{35}}{m^2}$ và có chiều dài là $\frac{6}{5}m$ $\frac{6}{5}m$ . Tính chiều rộng của hình chữ nhật đó.

Gợi ý đáp án:

Chiều rộng của hình chữ nhật đó là:

$\frac{{48}}{{35}}:\frac{6}{5} = \frac{{48}}{{35}}.\frac{5}{6} = \frac{{48.5}}{{35.6}} = \frac{{6.8.5}}{{7.5.6}} = \frac{8}{7}$ $\frac{{48}}{{35}}:\frac{6}{5} = \frac{{48}}{{35}}.\frac{5}{6} = \frac{{48.5}}{{35.6}} = \frac{{6.8.5}}{{7.5.6}} = \frac{8}{7}$ (m)

Vậy chiều rộng của hình chữ nhật là $\frac{8}{7}$ $\frac{8}{7}$ m

Giải Toán 6 Chân trời sáng tạo Thực hành

Thực hành 1

Tính giá trị biểu thức sau theo cách hợp lí:

$\left( {\frac{{20}}{7}.\frac{{ - 4}}{{ - 5}}} \right) + \left( {\frac{{20}}{7}.\frac{3}{{ - 5}}} \right)$ $\left( {\frac{{20}}{7}.\frac{{ - 4}}{{ - 5}}} \right) + \left( {\frac{{20}}{7}.\frac{3}{{ - 5}}} \right)$

Gợi ý đáp án:

Thực hiện phép tính:

$\begin{matrix} \left( {\dfrac{{20}}{7}.\dfrac{{ - 4}}{{ - 5}}} \right) + \left( {\dfrac{{20}}{7}.\dfrac{3}{{ - 5}}} \right) \hfill \\ = \left( {\dfrac{{20}}{7}.\dfrac{4}{5}} \right) + \left( {\dfrac{{20}}{7}.\dfrac{{ - 3}}{5}} \right) \hfill \\ = \dfrac{{20}}{7}.\left( {\dfrac{4}{5} + \dfrac{{ - 3}}{5}} \right) \hfill \\ = \dfrac{{20}}{7}.\dfrac{{4 + \left( { - 3} \right)}}{5} = \dfrac{{20}}{7}.\dfrac{1}{5} = \dfrac{{20.1}}{{7.5}} = \dfrac{{4.5}}{{7.5}} = \dfrac{4}{7} \hfill \\ \end{matrix}$ $\begin{matrix} \left( {\dfrac{{20}}{7}.\dfrac{{ - 4}}{{ - 5}}} \right) + \left( {\dfrac{{20}}{7}.\dfrac{3}{{ - 5}}} \right) \hfill \\ = \left( {\dfrac{{20}}{7}.\dfrac{4}{5}} \right) + \left( {\dfrac{{20}}{7}.\dfrac{{ - 3}}{5}} \right) \hfill \\ = \dfrac{{20}}{7}.\left( {\dfrac{4}{5} + \dfrac{{ - 3}}{5}} \right) \hfill \\ = \dfrac{{20}}{7}.\dfrac{{4 + \left( { - 3} \right)}}{5} = \dfrac{{20}}{7}.\dfrac{1}{5} = \dfrac{{20.1}}{{7.5}} = \dfrac{{4.5}}{{7.5}} = \dfrac{4}{7} \hfill \\ \end{matrix}$

Thực hành 2

Tính:

a) $\frac{{ - 2}}{7}:\frac{4}{7}$ $\frac{{ - 2}}{7}:\frac{4}{7}$

c) $4:\frac{{ - 2}}{5}$ $4:\frac{{ - 2}}{5}$

b) $\frac{{ - 4}}{5}:\frac{{ - 3}}{{11}}$ $\frac{{ - 4}}{5}:\frac{{ - 3}}{{11}}$

d) $\frac{{15}}{{ - 18}}:6$ $\frac{{15}}{{ - 18}}:6$

Gợi ý đáp án:

a) $\frac{{ - 2}}{7}:\frac{4}{7} = \frac{{ - 2}}{7}.\frac{7}{4} = \frac{{\left( { - 2} \right).7}}{{7.4}} = \frac{{ - 2}}{4} = \frac{{ - 1}}{2}$ $\frac{{ - 2}}{7}:\frac{4}{7} = \frac{{ - 2}}{7}.\frac{7}{4} = \frac{{\left( { - 2} \right).7}}{{7.4}} = \frac{{ - 2}}{4} = \frac{{ - 1}}{2}$

b) $\frac{{ - 4}}{5}:\frac{{ - 3}}{{11}} = \frac{{ - 4}}{5}.\frac{{11}}{{ - 3}} = \frac{{\left( { - 4} \right).11}}{{5.\left( { - 3} \right)}} = \frac{{ - 44}}{{ - 15}} = \frac{{44}}{{15}}$ $\frac{{ - 4}}{5}:\frac{{ - 3}}{{11}} = \frac{{ - 4}}{5}.\frac{{11}}{{ - 3}} = \frac{{\left( { - 4} \right).11}}{{5.\left( { - 3} \right)}} = \frac{{ - 44}}{{ - 15}} = \frac{{44}}{{15}}$

c) $4:\frac{{ - 2}}{5} = \frac{4}{1}.\frac{5}{{ - 2}} = \frac{{4.5}}{{1.\left( { - 2} \right)}} = - 10$ $4:\frac{{ - 2}}{5} = \frac{4}{1}.\frac{5}{{ - 2}} = \frac{{4.5}}{{1.\left( { - 2} \right)}} = - 10$

d) $\frac{{15}}{{ - 18}}:6 = \frac{{15}}{{ - 18}}.\frac{1}{6} = \frac{{15.1}}{{\left( { - 18} \right).6}} = \frac{{5.3}}{{\left( { - 6} \right).3.6}} = \frac{5}{{ - 36}} = - \frac{5}{{36}}$ $\frac{{15}}{{ - 18}}:6 = \frac{{15}}{{ - 18}}.\frac{1}{6} = \frac{{15.1}}{{\left( { - 18} \right).6}} = \frac{{5.3}}{{\left( { - 6} \right).3.6}} = \frac{5}{{ - 36}} = - \frac{5}{{36}}$

Giải Toán 6 Chân trời sáng tạo trang 20 tập 2

Bài 1

Tính giá trị của biểu thức

a) $(\frac{-2}{-5} : \frac{3}{-4}).\frac{4}{5}$ $(\frac{-2}{-5} : \frac{3}{-4}).\frac{4}{5}$
b) $\frac{-3}{-4} : (\frac{7}{-5}.\frac{-3}{2})$ $\frac{-3}{-4} : (\frac{7}{-5}.\frac{-3}{2})$
c) $\frac{-1}{9}.\frac{-3}{5}+\frac{5}{-6}.\frac{-3}{5}+\frac{5}{2}.\frac{-3}{5}$ $\frac{-1}{9}.\frac{-3}{5}+\frac{5}{-6}.\frac{-3}{5}+\frac{5}{2}.\frac{-3}{5}$

Hướng dẫn giải

Tính chất phân phối của phép nhân đối với phép cộng: a.(b + c) = a.b + a.c

Muốn nhân hai phân số ta nhân hai tử số với nhau và nhân hai mẫu số với nhau.
Muốn chia một phân số cho một phân số khác 0 ta nhân phân số thứ nhất với phân số có tử số là mẫu số của phân số thứ hai và mẫu số là tử số của phân số thứ hai.

Gợi ý đáp án:

a) $( \frac{-2}{-5} : \frac{3}{-4}).\frac{4}{5}$ $( \frac{-2}{-5} : \frac{3}{-4}).\frac{4}{5}$

$= (\frac{-2}{-5} . \frac{-4}{3}) . \frac{4}{5} = \frac{-2.-4}{-5.3}. \frac{4}{5}$ $= (\frac{-2}{-5} . \frac{-4}{3}) . \frac{4}{5} = \frac{-2.-4}{-5.3}. \frac{4}{5}$

$= \frac{-8}{15}. \frac{4}{5} = \frac{-8.4}{15.5} = \frac{-32}{75}$ $= \frac{-8}{15}. \frac{4}{5} = \frac{-8.4}{15.5} = \frac{-32}{75}$

b) $\frac{-3}{-4} : (\frac{7}{-5}.\frac{-3}{2})$ $\frac{-3}{-4} : (\frac{7}{-5}.\frac{-3}{2})$

$= \frac{3}{4} : \frac{7.-3}{-5.2} = \frac{3}{4}: \frac{21}{10}$ $= \frac{3}{4} : \frac{7.-3}{-5.2} = \frac{3}{4}: \frac{21}{10}$

$= \frac{3}{4}.\frac{10}{21} = \frac{3.10}{4.21} = \frac{30}{84}$ $= \frac{3}{4}.\frac{10}{21} = \frac{3.10}{4.21} = \frac{30}{84}$

c) $\frac{-1}{9}.\frac{-3}{5}+\frac{5}{-6}.\frac{-3}{5}+\frac{5}{2}.\frac{-3}{5}$ $\frac{-1}{9}.\frac{-3}{5}+\frac{5}{-6}.\frac{-3}{5}+\frac{5}{2}.\frac{-3}{5}$

$= \frac{-3}{5}. (\frac{1}{9} + \frac{-5}{6} + \frac{5}{2})$ $= \frac{-3}{5}. (\frac{1}{9} + \frac{-5}{6} + \frac{5}{2})$

$= \frac{-3}{5}. ( \frac{-2}{18} + \frac{-15}{18} + \frac{45}{18})$ $= \frac{-3}{5}. ( \frac{-2}{18} + \frac{-15}{18} + \frac{45}{18})$

$= \frac{-3}{5}. \frac{-2-15+45}{18} =\frac{-3}{5}.\frac{28}{18}$ $= \frac{-3}{5}. \frac{-2-15+45}{18} =\frac{-3}{5}.\frac{28}{18}$

$= \frac{-3.28}{5.18}= \frac{-84}{90}$ $= \frac{-3.28}{5.18}= \frac{-84}{90}$

Bài 2

Một ô tô chạy hết 8 phút trên một đoạn đường với vận tối trung bình 40km/h. Hãy tính độ dài đoạn đường đó. Người lái xe muốn thời gian chạy hết quãng đường đó chỉ 5 phút thì ô tô phải chạy với vận tốc trung bình là bao nhiêu?

Hướng dẫn giải

Quãng đường bằng vận tốc nhân với thời gian
Đổi 1 giờ = 60 phút
Muốn nhân hai phân số ta nhân hai tử số với nhau và nhân hai mẫu số với nhau.
Muốn chia một phân số cho một phân số khác 0 ta nhân phân số thứ nhất với phân số có tử số là mẫu số của phân số thứ hai và mẫu số là tử số của phân số thứ hai.

Gợi ý đáp án:

Đổi 8 phút = $\frac{2}{15}$ $\frac{2}{15}$ giờ

5 phút = $\frac{1}{12}$ $\frac{1}{12}$

Độ dài quãng đường đó là:

$\frac{2}{15}. 40 = \frac{16}{3}$ $\frac{2}{15}. 40 = \frac{16}{3}$ (km)

Người lái xe muốn thời gian chạy hết quãng đường đó chỉ 5 phút thì ô tô phải chạy với vận tốc trung bình là:

$\frac{16}{3} : \frac{1}{12} = 64$ $\frac{16}{3} : \frac{1}{12} = 64$ (km/h)

Đáp số: 64 km/h

Bài 3

Tính diện tích hình chữ nhật ABCD ở hình bên theo hai cách, trong đó có cách tính tổng diện tích các hình chữ nhật AEFD và EBCF. Hai cách đó minh họa tính chất nào của phép nhân phân số?

Bài 3

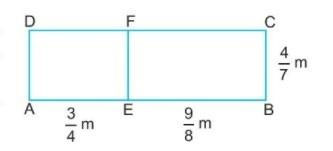
Hướng dẫn giải

Hình chữ nhật có các cặp cạnh đối song song và bằng nhau.
Diện tích hình chữ nhật bằng chiều dài nhân với chiều rộng.

Ngoài việc sử dụng công thức tính diện tích ta có thể tính diện tích hình chữ nhật bằng tổng diện tích các hình nhỏ.

Gợi ý đáp án:

Cách 1: Diện tích hình chữ nhật ABCD là:

$\frac{4}{7} . (\frac{3}{4} + \frac{9}{8}) = \frac{15}{14} (m^{2})$ $\frac{4}{7} . (\frac{3}{4} + \frac{9}{8}) = \frac{15}{14} (m^{2})$

=> Tính chất phân phối của phép nhân

Cách 2: Diện tích hình chữ nhật ABCD là:

$\frac{4}{7} . (\frac{3}{4} + \frac{9}{8}.\frac{4}{7} = \frac{4}{7} . (\frac{3}{4} + \frac{9}{8}) = \frac{15}{14} (m^{2})$ $\frac{4}{7} . (\frac{3}{4} + \frac{9}{8}.\frac{4}{7} = \frac{4}{7} . (\frac{3}{4} + \frac{9}{8}) = \frac{15}{14} (m^{2})$

=> Tính chất kết hợp của phép nhân

Đáp số: $\frac{15}{14} (m^{2})$ $\frac{15}{14} (m^{2})$

Lý thuyết Phép nhân và phép chia phân số

1. Phép nhân phân số

+ Muốn nhân hai phân số, ta nhân các tử số với nhau và nhân các mẫu với nhau.

$\dfrac{a}{b}.\dfrac{c}{d} = \dfrac{{a.c}}{{b.d}}$ $\dfrac{a}{b}.\dfrac{c}{d} = \dfrac{{a.c}}{{b.d}}$

+ Muốn nhân một số nguyên với một phân số (hoặc một phân số với một số nguyên), ta nhân số nguyên với tử của phân số và giữ nguyên mẫu: $a.\dfrac{b}{c} = \dfrac{{a.b}}{c}$ $a.\dfrac{b}{c} = \dfrac{{a.b}}{c}$

Ví dụ:

$\frac{-2}{7}.\frac{4}{-11}=\frac{\left(-2\right).4}{7.\left(-11\right)}=\frac{-8}{-77}=\frac{8}{77}$ $\frac{-2}{7}.\frac{4}{-11}=\frac{\left(-2\right).4}{7.\left(-11\right)}=\frac{-8}{-77}=\frac{8}{77}$

2. Phép chia phân số

Muốn chia một phân số hay một số nguyên cho một phân số, ta nhân số bị chia với số nghịch đảo của số chia.

$\dfrac{a}{b}:\dfrac{c}{d} = \dfrac{a}{b}.\dfrac{d}{c} = \dfrac{{a.d}}{{b.c}}$ $\dfrac{a}{b}:\dfrac{c}{d} = \dfrac{a}{b}.\dfrac{d}{c} = \dfrac{{a.d}}{{b.c}}$

$a:\dfrac{c}{d} = a.\dfrac{d}{c} = \dfrac{{a.d}}{c}\left( {c \ne 0} \right)$ $a:\dfrac{c}{d} = a.\dfrac{d}{c} = \dfrac{{a.d}}{c}\left( {c \ne 0} \right)$

Ví dụ: $\dfrac{{ - 1}}{6}:\dfrac{3}{{13}} = \dfrac{{ - 1}}{6}.\dfrac{{13}}{3} = \dfrac{{\left( { - 1} \right).13}}{{6.3}} = \dfrac{{ - 13}}{{18}}$ $\dfrac{{ - 1}}{6}:\dfrac{3}{{13}} = \dfrac{{ - 1}}{6}.\dfrac{{13}}{3} = \dfrac{{\left( { - 1} \right).13}}{{6.3}} = \dfrac{{ - 13}}{{18}}$

Trắc nghiệm Toán 6 Bài 5: Phép nhân và phép chia phân số

Câu 1: Chọn phát biểu đúng nhất trong các phát biểu sau:

A. Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
B. Phân số nào nhân với 11 cũng bằng chính nó.
C. Phân số nào nhân với 00 cũng bằng 00
D. Cả A, B, C đều đúng

Trả lời:

Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.

Phân số nào nhân với 11 cũng bằng chính nó.

Phân số nào nhân với 00 cũng bằng 00

Vậy cả A, B, C đều đúng.

Đáp án cần chọn là: D

Câu 2: Phép nhân phân số có những tính chất nào?

A. Tính chất giao hoán
B. Tính chất kết hợp
C. Tính chất nhân phân phối
D. Tất cả các tính chất trên

Trả lời:

Phép nhân phân số cũng có các tính chất tương tự phép nhân số tự nhiên như tính chất giao hoán, tính chất kết hợp, tính chất nhân phân phối.

Đáp án cần chọn là: D

Câu 3: Tính $\frac{1}{12}.\frac{8}{-9}$ $\frac{1}{12}.\frac{8}{-9}$

A. $\frac{-2}{27}$ $\frac{-2}{27}$

B. $\frac{-4}{9}$ $\frac{-4}{9}$

C. $\frac{-1}{18}$ $\frac{-1}{18}$

D. $\frac{-3}{2}$ $\frac{-3}{2}$

Trả lời:

$\frac{1}{12}.\frac{8}{-9}=\frac{1.8}{12.\left(-9\right)}\frac{1.2.4}{4.3.\left(-9\right)}=\frac{2}{-27}=\frac{-2}{27}$ $\frac{1}{12}.\frac{8}{-9}=\frac{1.8}{12.\left(-9\right)}\frac{1.2.4}{4.3.\left(-9\right)}=\frac{2}{-27}=\frac{-2}{27}$

Đáp án cần chọn là: A

Câu 4: Kết quả của phép tính $(−2).\frac{3}{8}$ $(−2).\frac{3}{8}$ là

A. $\frac{-16}{8}$ $\frac{-16}{8}$

B. $\frac{-13}{8}$ $\frac{-13}{8}$

C. $\frac{-6}{16}$ $\frac{-6}{16}$

D. $-\frac{3}{4}$ $-\frac{3}{4}$

Trả lời:

$(−2).\frac{3}{8} =\frac{(−2).3}{8} = \frac{−6}{8}= \frac{−3}{4}$ $(−2).\frac{3}{8} =\frac{(−2).3}{8} = \frac{−6}{8}= \frac{−3}{4}$

Đáp án cần chọn là: D

Chia sẻ bởi: