Toán 6 Bài 7: Hỗn số Giải Toán lớp 6 trang 24 sách Chân trời sáng tạo - Tập 2

Bài trước

Mục lục

Bài sau

Giải Toán lớp 6 Bài 7: Hỗn số bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 6 Tập 2 Chân trời sáng tạo trang 23, 24.

Lời giải Toán 6 Bài 7 Chân trời sáng tạo trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 6, từ đó học tốt môn Toán lớp 6 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài 7 Chương 5: Phân số. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 6 bài 7: Hỗn số

Giải Toán 6 Chân trời sáng tạo Hoạt động
Giải Toán 6 Chân trời sáng tạo Thực hành
- Thực hành 1
- Thực hành 2
Giải Toán 6 Chân trời sáng tạo trang 24 tập 2
Lý thuyết Hỗn số
Trắc nghiệm Toán 6 Bài 7: Hỗn số

Giải Toán 6 Chân trời sáng tạo Hoạt động

Ở chợ quê, người ta thường đổ bánh đúc trên đĩa có lót lá để tiện cho việc bán theo các phần khác nhau (xem hình). Thông thường mỗi đĩa bánh chia làm 4 phần.

Bánh

a) Chị An mua 5 phần bánh, được người bán lấy cho một đĩa và một phần, có đúng không?

b) Bà Bé mua 11 phần bánh, được người bán lấy cho hai đĩa và 3 phần, có đúng không?

Gợi ý đáp án:

a) Người bán lấy một đĩa (4 phần) và một phần.

Do đó, số phần người bán lấy ra là: 4 . 1 + 1 = 5 (phần)

Vậy chị An mua 5 phần, người bán lấy một đĩa và một phần là đúng.

b) Người bán lấy hai đĩa (mỗi đĩa 4 phần) và 3 phần.

Do đó, số phần người bán lấy ra là: 4 . 2 + 3 = 11 (phần)

Vậy bà Bé mua 11 phần, người bán lấy hai đĩa và 3 phần là đúng.

Giải Toán 6 Chân trời sáng tạo Thực hành

Thực hành 1

Viết phân số $\frac{{11}}{2}$ $\frac{{11}}{2}$ ở dưới dạng hỗn số và cho biết phần số nguyên, phần phân số.

Gợi ý đáp án:

Thực hiện phép tính như sau:

$\frac{{11}}{2} = \frac{{10 + 5}}{2} = \frac{{10}}{2} + \frac{5}{2} = 5 + \frac{5}{2} = 5\frac{5}{2}$ $\frac{{11}}{2} = \frac{{10 + 5}}{2} = \frac{{10}}{2} + \frac{5}{2} = 5 + \frac{5}{2} = 5\frac{5}{2}$

Phần nguyên là 5

Phần phân số là $\frac{5}{2}$ $\frac{5}{2}$

Thực hành 2

Tính giá trị của biểu thức $\left( {\frac{5}{{ - 4}} + 3\frac{1}{3}} \right):\frac{{10}}{9}$ $\left( {\frac{5}{{ - 4}} + 3\frac{1}{3}} \right):\frac{{10}}{9}$

Gợi ý đáp án:

Thực hiện phép tính như sau:

Cách 1: Thực hiện trong ngoặc trước

$\begin{matrix} \left( {\dfrac{5}{{ - 4}} + 3\dfrac{1}{3}} \right):\dfrac{{10}}{9} \hfill \\ = \left( {\dfrac{5}{{ - 4}} + \dfrac{{10}}{3}} \right):\dfrac{{10}}{9} \hfill \\ = \left( {\dfrac{5}{{ - 4}} + \dfrac{{10}}{3}} \right):\dfrac{{10}}{9} \hfill \\ = \left( {\dfrac{{ - 15}}{{12}} + \dfrac{{40}}{{12}}} \right):\dfrac{{10}}{9} \hfill \\ = \dfrac{{25}}{{12}}:\dfrac{{10}}{9} = \dfrac{{25.9}}{{10.12}} = \dfrac{{15}}{8} \hfill \\ \end{matrix}$ $\begin{matrix} \left( {\dfrac{5}{{ - 4}} + 3\dfrac{1}{3}} \right):\dfrac{{10}}{9} \hfill \\ = \left( {\dfrac{5}{{ - 4}} + \dfrac{{10}}{3}} \right):\dfrac{{10}}{9} \hfill \\ = \left( {\dfrac{5}{{ - 4}} + \dfrac{{10}}{3}} \right):\dfrac{{10}}{9} \hfill \\ = \left( {\dfrac{{ - 15}}{{12}} + \dfrac{{40}}{{12}}} \right):\dfrac{{10}}{9} \hfill \\ = \dfrac{{25}}{{12}}:\dfrac{{10}}{9} = \dfrac{{25.9}}{{10.12}} = \dfrac{{15}}{8} \hfill \\ \end{matrix}$

Cách 2: Thực hiện bỏ dấu ngoặc

$\begin{matrix} \left( {\dfrac{5}{{ - 4}} + 3\dfrac{1}{3}} \right):\dfrac{{10}}{9} \hfill \\ = \left( {\frac{5}{{ - 4}} + \dfrac{{10}}{3}} \right):\dfrac{{10}}{9} \hfill \\ = \left( {\dfrac{5}{{ - 4}} + \dfrac{{10}}{3}} \right):\dfrac{{10}}{9} \hfill \\ = \dfrac{5}{{ - 4}}:\dfrac{{10}}{9} + \dfrac{{10}}{3}:\dfrac{{10}}{9} \hfill \\ = \dfrac{5}{{ - 4}}.\dfrac{9}{{10}} + \dfrac{{10}}{3}.\dfrac{9}{{10}} = \dfrac{{ - 9}}{8} + 3 = \dfrac{{15}}{8} \hfill \\ \end{matrix}$ $\begin{matrix} \left( {\dfrac{5}{{ - 4}} + 3\dfrac{1}{3}} \right):\dfrac{{10}}{9} \hfill \\ = \left( {\frac{5}{{ - 4}} + \dfrac{{10}}{3}} \right):\dfrac{{10}}{9} \hfill \\ = \left( {\dfrac{5}{{ - 4}} + \dfrac{{10}}{3}} \right):\dfrac{{10}}{9} \hfill \\ = \dfrac{5}{{ - 4}}:\dfrac{{10}}{9} + \dfrac{{10}}{3}:\dfrac{{10}}{9} \hfill \\ = \dfrac{5}{{ - 4}}.\dfrac{9}{{10}} + \dfrac{{10}}{3}.\dfrac{9}{{10}} = \dfrac{{ - 9}}{8} + 3 = \dfrac{{15}}{8} \hfill \\ \end{matrix}$

Giải Toán 6 Chân trời sáng tạo trang 24 tập 2

Bài 1

Dùng hỗn số viết thời gian ở đồng hồ trong các hình vẽ sau:

Bài 1

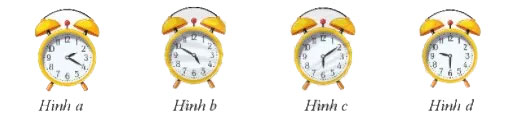
Thời gian ở Hình a có thể viết là $2\frac{1}{3}$ $2\frac{1}{3}$ giờ hoặc $14\frac{20}{60}$ $14\frac{20}{60}$ giờ được không?

Gợi ý đáp án:

Hình a: $2\frac{1}{3}$ $2\frac{1}{3}$

Hình b: $5\frac{5}{6}$ $5\frac{5}{6}$

Hình c: $6\frac{1}{6}$ $6\frac{1}{6}$

Hình d: $9\frac{1}{2}$ $9\frac{1}{2}$

Bài 2

Sắp xếp các khối lượng sau theo thứ tự từ lớn đến nhỏ:

$3\frac{3}{4}$ $3\frac{3}{4}$ tạ; $\frac{377}{100}$ $\frac{377}{100}$ tạ; $\frac{7}{2}$ $\frac{7}{2}$ tạ ; $3\frac{45}{100}$ $3\frac{45}{100}$ tạ; 365 kg

Gợi ý đáp án:

Các khối lượng theo thứ tự từ lớn đến nhỏ:

$\frac{377}{100}$ $\frac{377}{100}$ tạ; $3\frac{3}{4}$ $3\frac{3}{4}$ tạ; 365 kg; $\frac{7}{2}$ $\frac{7}{2}$ tạ ; $3\frac{45}{100}$ $3\frac{45}{100}$ tạ

Bài 3

Dùng phân số hoặc hỗn số để viết các đại lượng diện tích dưới đây theo mét vuông:

a) $125 dm^{2}$ $125 dm^{2}$ b) $218 cm^{2}$ $218 cm^{2}$ c) $240 dm^{2}$ $240 dm^{2}$ d) $34 cm^{2}$ $34 cm^{2}$

Nếu viết chúng theo đề xi mét vuông thì sao?

Gợi ý đáp án:

a) $1\frac{25}{100} m^{2}$ $1\frac{25}{100} m^{2}$ b) $\frac{109}{5000}m^{2}$ $\frac{109}{5000}m^{2}$ c) $2\frac{40}{100}m^{2}$ $2\frac{40}{100}m^{2}$ d) $\frac{17}{5000}m^{2}$ $\frac{17}{5000}m^{2}$

Nếu viết chúng theo đề xi mét vuông:

a) $\frac{125}{1}dm^{2}$ $\frac{125}{1}dm^{2}$ b) $2\frac{18}{100} dm^{2}$ $2\frac{18}{100} dm^{2}$ c) $\frac{240}{1}dm^{2}$ $\frac{240}{1}dm^{2}$ d) $\frac{34}{100}dm^{2}$ $\frac{34}{100}dm^{2}$

Bài 4

Hai xe ô tô cùng đi được quãng đường 100 km, xe taxi chạy trong $1\frac{1}{5}$ $1\frac{1}{5}$ giờ và xe tải chạy trong 70 phút. So sánh vận tốc hai xe.

Gợi ý đáp án:

Đổi 70 phút = $1\frac{1}{6}$ $1\frac{1}{6}$ giờ

Vận tốc của xe taxi là:

$100 : 1\frac{1}{5} = 100 : \frac{6}{5} = 83\frac{1}{3} (km/h)$ $100 : 1\frac{1}{5} = 100 : \frac{6}{5} = 83\frac{1}{3} (km/h)$

Vận tốc của xe taxi là:

$100 : 1\frac{1}{6} = 85\frac{5}{7} (km/h)$ $100 : 1\frac{1}{6} = 85\frac{5}{7} (km/h)$

Ta có: $85\frac{5}{7} > 83\frac{1}{3}$ $85\frac{5}{7} > 83\frac{1}{3}$ nên vận tốc của xe taxi lớn hơn.

Lý thuyết Hỗn số

Định nghĩa:

Cho a và b là hai số nguyên dương, a > b, a không chia hết cho b. Nếu a chia cho b được thương là q và số dư là r, thì ta viết $\dfrac{a}{b} = q\dfrac{r}{b}$ $\dfrac{a}{b} = q\dfrac{r}{b}$ và gọi $q\dfrac{r}{b}$ $q\dfrac{r}{b}$ là hỗn số.

Đọc là “q, r phần b”.

Ví dụ:

Phép chia 23:4 có thương là 5 và số dư là 3 nên ta có: $\dfrac{{23}}{4} = 5\dfrac{3}{4}$ $\dfrac{{23}}{4} = 5\dfrac{3}{4}$.

Đọc là: “ năm, ba phần tư”.

Chú ý:

Với hỗn số $q\dfrac{r}{b}$ $q\dfrac{r}{b}$ người ta gọi q là phần số nguyên và $\dfrac{r}{b}$ $\dfrac{r}{b}$ là phần phân số của hỗn số.

Ví dụ:

Hỗn số $5\dfrac{3}{4}$ $5\dfrac{3}{4}$ có phần nguyên là 5 và phần phân số là $\dfrac{3}{4}$ $\dfrac{3}{4}$.

Trắc nghiệm Toán 6 Bài 7: Hỗn số

Câu 1: Viết phân số $\frac{4}{3}$ $\frac{4}{3}$ dưới dạng hỗn số ta được

A. $1\frac{2}{3}$ $1\frac{2}{3}$

B. $3\frac{1}{3}$ $3\frac{1}{3}$

C. $3\frac{1}{4}$ $3\frac{1}{4}$

D. $1\frac{1}{3}$ $1\frac{1}{3}$

Đáp án: D

Câu 2: Hai xe ô tô cùng đi được quãng đường 100 km, xe taxi chạy trong $1\frac{1}{5}$ $1\frac{1}{5}$ giờ và xe tải chạy trong 70 phút. So sánh vận tốc hai xe.

A. Vận tốc xe tải lớn hơn vận tốc xe taxi

B. Vận tốc xe taxi lớn hơn vận tốc xe tải

C. Vận tốc hai xe bằng nhau

D. Không so sánh được

Đáp án: B

Chia sẻ bởi: