Toán 6 Bài 4: Lũy thừa với số mũ tự nhiên Giải Toán lớp 6 trang 18 - Tập 1 sách Chân trời sáng tạo

Giải bài tập Toán lớp 6 Bài 4: Lũy thừa với số mũ tự nhiên với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 6 Tập 1 Chân trời sáng tạo trang 16, 17, 18. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 6 Bài 4 chi tiết, còn giúp các em hệ thống lại toàn bộ kiến thức lý thuyết trọng tâm của Bài 4 Chương 1: Số tự nhiên. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Phần Hoạt động khởi động

Gợi ý đáp án:

Sau bài học này ta sẽ biết được:  

Phần Hoạt động khám phá

Hoạt động 1 trang 16 Toán 6 tập 1

Viết gọn các tích sau bằng cách dùng lũy thừa

a) 5 . 5 . 5

b) 7 . 7. 7. 7. 7. 7

Gợi ý đáp án:

a) 5 . 5 . 5 = 5 ³

b) 7 . 7. 7. 7. 7. 7 = 7 ⁶

Hoạt động 2 trang 17 Toán 6 tập 1

Viết tích của hai lũy thừa sau thành một lũy thừa.

a) 3.3³

b) 2².2⁴

Gợi ý đáp án:

a) 3 . 3 ³ = 3 ^{1 + 3} = 3 ⁴

b) 2 ² . 2 ⁴ = 2 ^{2 + 4} = 2 ⁶

Hoạt động 3 trang 17 Toán 6 tập 1

a) Từ phép tính 5².5⁵ = 5⁷, em hãy suy ra kết quả của mỗi phép tính 5⁷:5² và 5⁷:5⁵. Giải thích.

b) Hãy nhận xét về mối liên hệ giữa số mũ của lũy thừa vừa tìm được với số mũ của lũy thừa của số bị chia và số chia trong mỗi phép tính ở trên.

Từ nhận xét đó, hãy dự đoán kết quả của mỗi phép tính sau: 7⁹:7² và 6⁵:6³.

Gợi ý đáp án:

a) 5 ⁷ : 5 ² = 5 ^{7 − 2} = 5 ⁵

5 ⁷ : 5 ⁵ = 5 ^{7 − 5} = 5 ²

b) Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ.

Số mũ của lũy thừa vừa tìm được là hiệu, số mũ của lũy thừa số bị chia là số bị trừ, số mũ của lũy thừa số chia là số trừ trong phép trừ các số mũ.

Từ đó ta tính:

7 ⁹ : 7 ² = 7 ^{9 − 2} = 7 ⁷

6 ⁵ : 6 ³ = 6 ^{5 − 3} = 6 ²

Phần Thực hành

Thực hành 1 trang 17 Toán 6 tập 1

Viết các tích sau dưới dạng lũy thừa

a) 3 . 3 . 3

6 . 6 . 6 . 6

b) Phát biểu hoàn thiện các câu sau

3 ² còn gọi là 3.... hay .......của 3

5³ còn gọi là 5.... hay ..... của 5

c) Hãy đọc các lũy thừa sau và chỉ rõ cơ số, số mũ 3 ¹⁰ ; 10 ⁵

Gợi ý đáp án:

a) 3 . 3 . 3 = 3 ³

6 . 6 . 6 . 6 = 6 ⁴

b) 3 ² còn gọi là 3 mũ 2 hay lũy thừa bậc 2 của 3

5³ còn gọi là 5 mũ 3 hay lũy thừa bậc 3 của 5

c) 3 ¹⁰ đọc là 3 mũ 10, 3 lũy thừa 10 hay lũy thừa bậc 10 của 3

=> 3 ¹⁰ thì 3 là cơ số, 10 là số mũ.

10 ⁵ đọc là 10 mũ 5, 10 lũy thừa 5 hay lũy thừa bậc 5 của 10

=> 10 ⁵ thì 10 là cơ số, 5 là số mũ.

Thực hành 2 trang 17 Toán 6 tập 1

Gợi ý đáp án:

3 ³ . 3 ⁴ = 3 ^{3 + 4} = 3 ⁷

10 ⁴ . 10 ³ = 10 ^{4 + 3} = 10 ⁷

x ² . x ⁵ = x ^{2 + 5} = x ⁷

Thực hành 3 trang 17 Toán 6 tập 1

Gợi ý đáp án:

a) 11 ⁷ : 11 ³ = 11 ^{7 − 3} = 11 ⁴

11 ⁷ : 11 ⁷ = 11 ^{7 − 7} = 11 ⁰ = 1

7 ² . 7 ⁴ = 7 ^{2 + 4} = 7 ⁶

7 ² . 7 ⁴ : 7 ³ = 7 ^{2 + 4 − 3} = 7 ³

b) 9 ⁷ : 9 ² = 9 ⁵ => Đúng.

7 ¹⁰ : 7 ² = 7 ⁵ => Sai. 7 ¹⁰ : 7 ² = 7 ^{10 − 2} = 7 ⁸ .

2 ¹¹ : 2 ⁸ = 6=> Sai. 2 ¹¹ : ^{2 8} = 2 ^{11 − 8} = 2 ³ = 8.

5 ⁶ : 5 ⁶ = 5 => Sai. 5 ⁶ : 5 ⁶ = 1.

Phần Bài tập

Bài 1 trang 18 Toán 6 tập 1

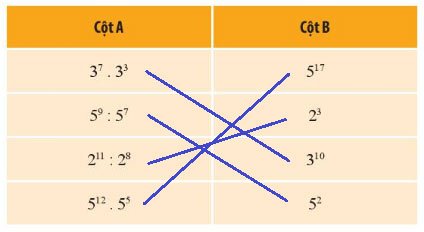
Ghép mỗi phép tính ở cột A với lũy thừa tương ứng của nó ở cột B.

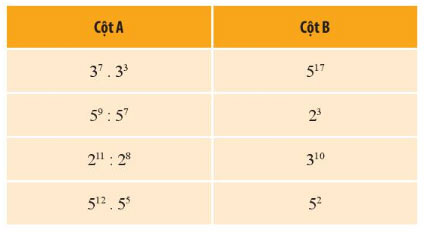
Gợi ý đáp án:

Bài 2 trang 18 Toán 6 tập 1

a) Viết kết quả của mỗi phép tính sau dưới dạng một lũy thừa:

b) Viết cấu tạo thập phân của các số 4 983, 54 297, 2 023 theo mẫu sau:

\(\begin{matrix} 4983 = 4.1000 + 9.100 + 8.10 + 3 \hfill \\ = {4.10^3} + {9.10^2} + 8.10 + 3 \hfill \\ \end{matrix}\)

Gợi ý đáp án:

a.

\(\begin{matrix} {5^7}{.5^5} = {5^{7 + 5}} = {5^{12}} \hfill \\ {9^5}:{8^0} = {9^5}:1 = {9^5} \hfill \\ {2^{10}}:64.16 = {2^{10}}:{2^6}{.2^4} = {2^{10 - 6 + 4}} = {2^8} \hfill \\ \end{matrix}\)

b.

\(\begin{matrix} 54297 = 50000 + 4000 + 200 + 90 + 7 \hfill \\ = 5.10000 + 4.1000 + 2.100 + 9.10 + 7 \hfill \\ = {5.10^4} + {4.10^3} + {2.10^2} + 9.10 + 7 \hfill \\ \end{matrix}\)

\(\begin{matrix} 2023 = 2000 + 20 + 3 \hfill \\ = 2.1000 + 2.10 + 3 \hfill \\ = {2.10^3} + 2.10 + 3. \hfill \\ \end{matrix}\)

Bài 3 trang 18 Toán 6 tập 1

Theo Tổng cục Thống kê, tháng 10 năm 2020 dân số Việt Nam được làm tròn là 98 000 000 người. Em hãy viết dân số của Việt Nam dưới dạng tích của một số với một lũy thừa của 10.

Gợi ý đáp án:

Dân số của Việt Nam tháng 10 năm 2020 viết dưới dạng tích của một số với một lũy thừa của 10 là:

98 000 000 = 98 . 1 000 000 = 98 . 10⁶

Bài 4 trang 18 Toán 6 tập 1

Biết rằng khối lượng của Trái Đất khoảng \(\underbrace {600...00}_{21{\text{ so 0}}}\) tấn, khối lượng của Mặt Trăng khoảng \(\underbrace {7500...00}_{{\text{18 so 0}}}\) tấn.

a) Em hãy viết khối lượng của Trái Đất và khối lượng của Mặt Trăng dưới dạng tích của một số với một tích của một số với một lũy thừa của 10.

b) Khối lượng Trái Đất gấp bao nhiêu lần khối lượng Mặt Trăng?

Gợi ý đáp án:

a. Khối lượng của Mặt Trời là: \(\underbrace {600...00}_{21{\text{ so 0}}} = {6.10^{21}}\)

Khối lượng của Mặt Trăng là: \(\underbrace {7500...00}_{{\text{18 so 0}}} = {75.10^{18}}\) hoặc có thể viết \(\underbrace {7500...00}_{{\text{18 so 0}}} = {750.10^{17}}\)

b. Khối lượng Mặt Trời gấp khối lương Mặt Trăng số lần là:

\({6.10^{21}}:{75.10^{18}} = \left( {6:75} \right).\left( {{{10}^{21}}:{{10}^{18}}} \right) = \frac{2}{{25}}{.10^{21 - 18}} = \frac{2}{{25}}{.10^3}\) (lần)

Đáp số: \(\frac{2}{{25}}{.10^3}\) lần

Lý thuyết Bài 4: Lũy thừa với số mũ tự nhiên

1. Lũy thừa

Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a.

aⁿ = a . a ….. a (n thừa số a) (n ∈ ℕ* )

Ta đọc aⁿ là “a mũ n” hoặc “lũy thừa bậc n của”.

Số a được gọi là cơ số, n được gọi là số mũ.

Ví dụ: 8⁵ đọc là “tám mũ năm”, có cơ số là 8 và số mũ là 5.

Phép nhân nhiều thừa số giống nhau như trên được gọi là phép nâng lên lũy thừa.

Đặc biệt, a² còn được đọc là “a bình phương” hay “bình phương của a”.

a³ được đọc là “a lập phương” hay “lập phương của a”.

Quy ước: a¹ = a.

Ví dụ:

a) Tính 2³ và 10³.

b) Viết 10 000 000 dưới dạng lũy thừa của 10.

c) Viết 16 dưới dạng lũy thừa cơ số 4

Hướng dẫn giải

a) Số 2³ là lũy thừa bậc 3 của 2 và là tích của 3 thừa số 2 nhân với nhau nên ta có:

2³ = 2 . 2 . 2 = 8.

Số 10³ là lũy thừa bậc 3 của 10 và là tích của 3 thừa số 10 nhân với nhau nên ta có:

10³ = 10 . 10 . 10 = 1 000.

b) Số 10 000 000 được viết dưới dạng lũy thừa của 10 là:

10 000 000 = 10 . 10 . 10 . 10 . 10 . 10 . 10 = 10⁷.

c) Số 16 được viết dưới dạng lũy thừa cơ số 4 là:

16 = 4 . 4 = 4².

2. Nhân hai lũy thừa cùng cơ số

Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.

a^m . aⁿ = a^{m + n}.

Ví dụ:

a) 3 . 3⁵ = 3¹ . 3⁵ = 3^{1 + 5} = 3⁶

b) 5² . 5⁴ = 5^{2 + 4} = 5⁶

c) a³ . a⁵ = a^{3 + 5} = a⁸.

3. Chia hai lũy thừa cùng cơ số

Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ.

a^m : aⁿ = a^{m – n} (a ≠ 0; m ≥ n ≥ 0).

Quy ước: a⁰ = 1 (a ≠ 0).

Ví dụ:

a) a⁶ : a² = a^{6 − 2} = a⁴ (a ≠ 0)

b) 2³ : 2³ = 2^{3 − 3} = 2⁰ = 1

c) 81 : 3² = 3⁴ : 3² = 3^{4 − 2} = 3² = 3 . 3 = 9.