™
Download.vn Học tập Lớp 8 Toán 8 Chân trời sáng tạo

Giải Toán 8 Bài 9: Ứng dụng thực tế của tam giác đồng dạng Giải SGK Toán 8 Hình học Tập 2 (trang 87)

Tải về Bình luận
  • 2
Mục lục

Giải bài tập SGK Toán 8 trang 87 giúp các em học sinh lớp 8 xem gợi ý giải các bài tập của Bài 9: Ứng dụng thực tế của tam giác đồng dạng Hình học 8 Chương 3. Qua đó các em sẽ nhanh chóng hoàn thiện toàn bộ bài tập của bài 9 Chương III Hình học 8 tập 2.

Giải bài tập Toán Hình 8 tập 2 Bài 9 Chương III: Ứng dụng thực tế của tam giác đồng dạng

Lý thuyết bài 9: Ứng dụng thực tế của tam giác đồng dạng

1. Đo gián tiếp chiều cao của vật

Giả sử cần phải xác định chiều cao của một tòa nhà, của một ngọn tháp hay của một cây nào đó, ta có thể làm như sau:

Tiến hành đo đạc

  • Đặt cọc AC đứng thẳng trên đó có gắn thước ngắm quay được quanh một cái chốt của cọc.
  • Điều chỉnh thước ngắm sao cho hướng thước đi qua đỉnh C' của cây (hoặc tháp), sau đó xác định giao điểm B của đường thẳng CC' và AA'.
  • Đo khoảng cách BA và BA'.

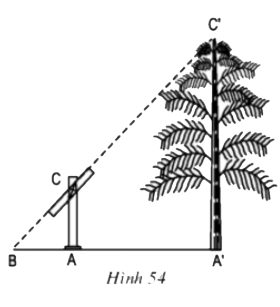
Đo gián tiếp chiều cao của vật

Tính chiều cao cây (hoặc tháp)

  • Ứng dụng tam giác đồng dạng, ta có: \Delta ABC \sim \Delta AΔABC∼ΔA′BC′ với tỉ số đồng dạng k=\frac{AC}{Ak=ACA′C′

=> AA′C′=k.AC

2. Đo khoảng cách giữa hai địa điểm trong đó có một địa điểm không thể tới được

Giả sử phải đo khoảng cách AB trong đó địa điểm A có ao hồ bao bọc không thể tới được.

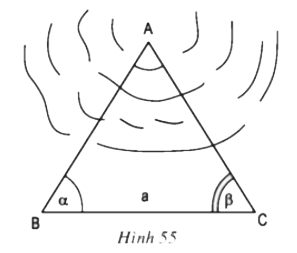
Đo gián tiếp chiều cao của vật

Tiến hành đo đạc

  • Chọn một khoảng đất bằng phẳng rồi vạch một đoạn BC và đo độ dài của nó (BC = a).
  • Dùng thước đo góc (giác kế) đo các góc: \widehat{ABC}=\alpha ,\widehat{ACB}=\betaABC^=α,ACB^=β.

Tính khoảng cách AB

  • Vẽ trên giấy tam giác A'B'C' sao cho: BB′C′=a′;B′^=α,C′^=β.
  • Khi đó, \Delta ABC \sim \Delta AΔABC∼ΔA′B′C theo tỉ số đồng dạng k=\frac{AB}{Ak=ABA′B′.
  • Thay số vào ta tính được AB.

Đo gián tiếp chiều cao của vật

Giải bài tập toán 8 trang 87 tập 2

Bài 53 (trang 87 SGK Toán 8 Tập 2)

Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao 2m và đặt xa cây 15m. Sau khi người ấy lùi ra xa cách cọc 0,8m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu, biết rằng khoảng cách từ chân đến mắt người ấy là 1,6m?

Xem gợi ý đáp án

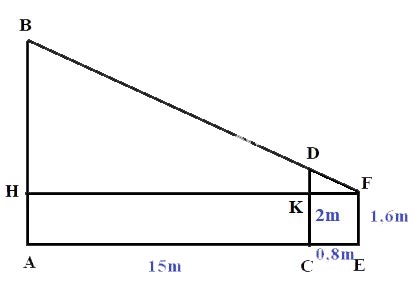
Bài 53

Giả sử AB là cây cần đo, CD là cọc EF là khoảng cách từ mắt tới chân.

Ta có: AC=15m, CE=0,8m, EF=1,6m, CD=2m và HACK, CEFK là các hình chữ nhật.

Ta có: KD // HB (giả thiết)

(Theo định lí)

\Rightarrow \dfrac{HB}{KD}= \dfrac{HF}{KF}⇒HBKD=HFKF (tính chất hai tam giác đồng dạng)

\Rightarrow HB = \dfrac{HF.KD}{KF}⇒HB=HF.KDKF

mà HF = HK + KF =AC + CE= 15 + 0,8 = 15,8m

KD = CD - CK = CD - EF = 2 - 1,6 = 0,4 m

Do đó: HB = 15,8 . 0,4 : 0,8 = 7,9 m

Vậy chiều cao của cây là AB = HB + AH = 7,9 + 1,6 = 9,5 m.

Bài 54 (trang 87 SGK Toán 8 Tập 2)

Để đo khoảng cách giữa hai điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính khoảng cách AB như hình 57; AB // DF; AD = m;DC = n; DF = a.

a) Em hãy nói rõ cách đo như thế nào.

b) Tính độ dài x của khoảng cách AB.

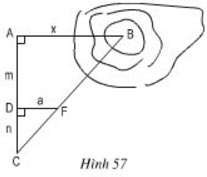
Bài 54

Xem gợi ý đáp án
a) Cách đo:

+ Tạo một tia Ay trên mặt đất vuông góc với tia AB.

+ Trên tia Ay lấy điểm C bất kì.

+ Chọn điểm F sao cho F nằm giữa B và C.

+ Từ F hạ FD vuông góc với AC (D nằm trên AC).

+ Đo các cạnh AD, DC, DF ta tính được khoảng cách AB.

b) Có DF // AB (cùng vuông góc với AC theo cách dựng) nên ∆CDF ∽ ∆CAB

\Rightarrow \dfrac{DF}{AB}=\dfrac{CD}{CA}⇒DFAB=CDCA (tính chất 2 tam giác đồng dạng)

\Rightarrow AB = \dfrac{DF.CA}{CD}= \dfrac{a(m+n)}{n}⇒AB=DF.CACD=a(m+n)n

Vậy x= \dfrac{DF.CA}{CD}= \dfrac{a(m+n)}{n}x=DF.CACD=a(m+n)n

Bài 55 (trang 87 SGK Toán 8 Tập 2)

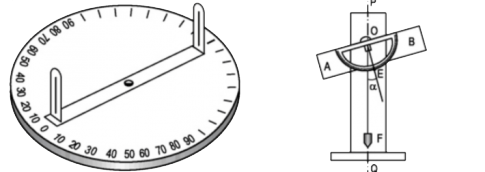
Hình 58 dưới đây mô tả dụng cụ đo bề dày của một số loại sản phẩm. Dụng cụ này gồm thước AC được chia đến 1mm và gắn với một bản kim loại hình tam giác ABD, khoảng cách BC = 10mm.

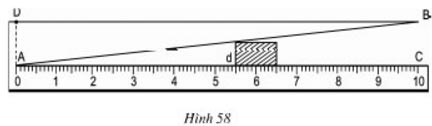
Bài 55

Muốn đo bề dày của vật, ta kẹp vật vào giữa bản kim loại và thước (đáy của vật áp vào bề mặt của thước AC). Khi đó, trên thước AC ta đọc được "bề dày" d của vật (trên hình vẽ ta có có d = 5,5mm).

Hãy chỉ rõ định lí nào của hình học là cơ sở để ghi các vạch trên thước AC (d ≤ 10mm)

Xem gợi ý đáp án

Theo hình vẽ thì B'C'//BC nên ∆ABC ∽ ∆AB'C' (theo định lí)

\Rightarrow \dfrac{AC⇒AC′AC=B′C′BC

B'C' là bề dày của vật cần đo

Vì d ≤ 10 mm nên BC=10mm=1cm

\Rightarrow B⇒B′C′=AC′.BCAC=110AC′

Vậy khi AC' = 5,5cm thì đọc BB′C′=110.5,5cm=0,55cm=5,5mm.

Dụng cụ trên đã dùng tính chất hai tam giác đồng dạng thì cạnh tương ứng tỉ lệ.

Chia sẻ bởi: 👨 Lê Thị tuyết Mai
Liên kết tải về
Tìm thêm: Toán lớp 8 Toán 8 Giải SGK Toán 8 SGK Toán 8
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
👨

Tài liệu tham khảo khác

Chủ đề liên quan

Có thể bạn quan tâm

Xem thêm

Mới nhất trong tuần

Tìm bài trong mục này
Đóng
Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ
Chia sẻ
Chia sẻ FacebookChia sẻ Twitter
Đóng