Toán 8 Bài 28: Hàm số bậc nhất và đồ thị của hàm số bậc nhất Giải Toán 8 Kết nối tri thức tập 2 trang 47, 48, 49, 50

Bài trước

Mục lục

Bài sau

Toán 8 Bài 28: Hàm số bậc nhất và đồ thị của hàm số bậc nhất là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Kết nối tri thức với cuộc sống tập 2 trang 47, 48, 49, 50.

Giải Toán 8 Kết nối tri thức tập 2 trang 47 → 50 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 28 Chương VII: Phương trình bậc nhất và hàm số bậc nhất. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Toán 8 Bài 28: Hàm số bậc nhất và đồ thị của hàm số bậc nhất Kết nối tri thức

Giải Toán 8 Kết nối tri thức Tập 2 trang 50

Giải Toán 8 Kết nối tri thức Tập 2 trang 50

Bài 7.24

Trong các hàm số sau, những hàm số nào là hàm số bậc nhất? Hãy xác định các hệ số a, b của chúng

a) $y=0.x-5$ b) $y=1-3x$ c) $y=-0,6x$

d) $y=\sqrt{2}(x-1)+3$ $y=\sqrt{2}(x-1)+3$ e) $y=2x^{2}+1$ $y=2x^{2}+1$

Lời giải:

Những hàm số bậc nhất là

b) $y=1-3x$ với $a=-3$, $b=1$

c) $y=-0,6x$ với $a=-0,6$, $b=0$

d) $y=\sqrt{2}(x-1)+3$ $y=\sqrt{2}(x-1)+3$ với $a=\sqrt{2}$ $a=\sqrt{2}$, $b=3-\sqrt{2}$ $b=3-\sqrt{2}$

Bài 7.25

Cho hàm số bậc nhất $y=ax+3$

a) Tìm hệ số a, biết rằng khi $x=1$ thì $y=5$

b) Với giá trị a tìm được, hãy hoàn thành bảng giá trị sau vào vở

x	-2	-1	0	1	2
y	?	?	?	?	?

Lời giải:

a) Có $x=1$, $y=5$ => $5=a+3$ => $a=2$

x	-2	-1	0	1	2
y	-1	1	3	5	7

Bài 7.26

Vẽ đồ thị của các hàm số sau

a) $y=2x-6$ b) $y=-3x+5$ c) $y=\frac{3}{2}x$ $y=\frac{3}{2}x$

Lời giải:

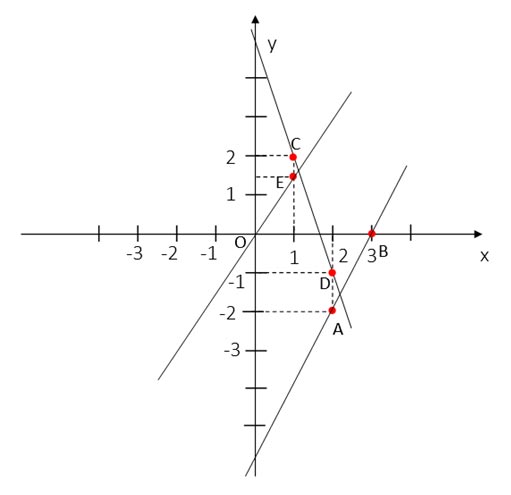
a) $y=2x-6$

Cho $x=2$ thì $y=-2$ ta có A(2;-2)

$x=3$ thì $y=0$, ta có B(3;0)

Đồ thị của hàm số $y=2x-6$ là đường thẳng AB

b) $y=-3x+5$

Cho $x=1$ thì $y=2$ ta có C(1;2)

$x=2$ thì $y=-1$, ta có D(2;-1)

Đồ thị của hàm số $y=-3x+5$ là đường thẳng CD

c) $y=\frac{3}{2}x$ $y=\frac{3}{2}x$

Cho $x=0$ thì $y=0$ ta có điểm ở gốc tọa độ O(0;0)

$x=1$ thì $y=\frac{3}{2}$ $y=\frac{3}{2}$, ta có $E(1;\frac{3}{2})$ $E(1;\frac{3}{2})$

Đồ thị của hàm số $y=-3x+5$ là đường thẳng OE

Bài 7.26

Bài 7.27

Đồng euro (EUR) là đơn vị tiền tệ chính thức ở một số quốc gia thành viên của Liên minh châu Âu. Vào một ngày, tỉ giá hối đoái giữa đồng euro và đồng đô là Mỹ (USD) là: 1EUR = 1,1052 USD

a) Viết công thức để chuyển đổi x euro sang y đô la Mỹ. Công thức tính y theo x này có phải là một hàm số bậc nhất của x không?

b) Vào ngày đó, 200 euro có giá trị bằng bao nhiêu đô la Mỹ?

c) Vào ngày đó, 500 đô la Mỹ có giá trị bằng bao nhiêu euro?

Lời giải:

a) $y=1,1052x$. Công thức tính y này là một hàm số bậc nhất của x

b) Vào ngày đó 200 euro có giá trị bằng 221,04 đo la Mỹ

c) Vào ngày đó 500 đô là Mỹ có giá trị bằng khoảng 452,407 euro

Bài 7.28

Giá cước điện thoại cố định của một hãng viễn thông bao gồm cước thuê bao là 22 000 đồng/tháng và cước gọi là 800 đồng/ phút

a) Lập công thức tính số điện cước điện thoại y (đồng) phải trả trong tháng khi gọi x phút

b) Tính số tiền cước điện thoại phải trả khi gọi 75 phút

c) Nếu số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi bao nhiêu phút

Lời giải:

a) $y=800x+22000$

b)Số tiền cước điện thoại phải trả khi gọi 75 phút: $y=800.75+22000=82000$ (đồng)

c) Nếu số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi trong:

$94000=800x+22000$ => $x=90$ (phút)

Bài 7.29

Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất $y=ax+b$, trong đó b biểu thị chi phí cố định của hoạt động kinh doanh và hệ số a biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố định hằng ngày là 36 triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là 1,8 triệu đồng.

a) Viết công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày

b) Vẽ đồ thị hàm số thu được ở câu a

c) Chi phí để sản xuất 15 chiếc xe đạp trong một ngày là bao nhiêu

d) Có thể sản xuất bao nhiêu chiếc xe đạp trong ngày, nếu chi phí trong ngày đó là 72 triệu đồng?

Lời giải:

a) Công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày: $y=1,8x+36$

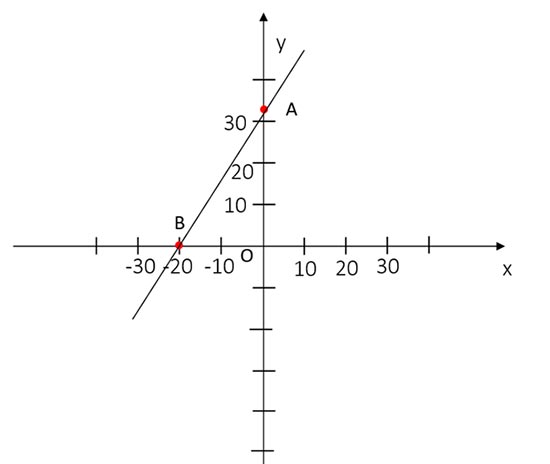
b) Cho x=0 thì y=36 ta có A(0;36)

y=0 thì x=-20, ta có B(-20;0)

Đồ thi của hàm số là đường thẳng AB

Bài 7.29