Toán 8 Bài 36: Các trường hợp đồng dạng của hai tam giác vuông Giải Toán 8 Kết nối tri thức tập 2 trang 98, 99, 100, 101, 102, 103

Giải bài tập Toán 8 Bài 36: Các trường hợp đồng dạng của hai tam giác vuông với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa SGK Toán 8 Kết nối tri thức với cuộc sống tập 2 trang 98, 99, 100, 101, 102, 103. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 8 Bài 36 chi tiết, còn giúp các em hệ thống lại toàn bộ kiến thức trọng tâm của Bài 36 Chương IX: Tam giác đồng dạng. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 8 Kết nối tri thức Tập 2 trang 102 - Vận dụng

Bác Minh muốn thay chiếc ti vi có chiều ngang của màn hình là 72cm (loại 32 inch) bằng chiếc ti vi mới loại 55 inch có cùng tỉ lệ khung hình (tỉ lệ giữa hai kích thước màn hình). Hỏi nếu khoảng trống đặt ti vi là một hình vuông cạnh 1m thì có thể đặt chiếc tivi mới vào đó không?

Lời giải:

Hình minh họa:

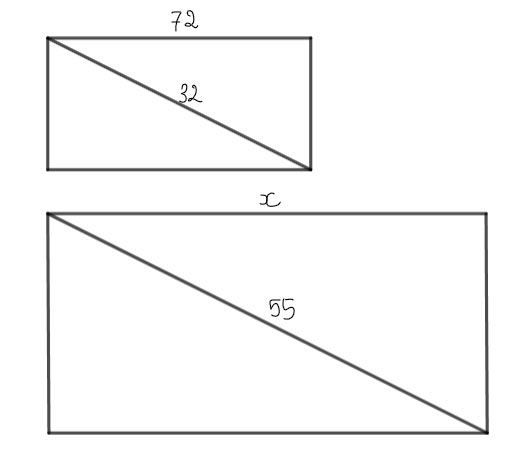
Đơn vị đường chéo: inch

Đơn vị hai cạnh của màn hình: cm

Gọi x (cm) là độ dài của chiều ngang màn hình chiếc ti vi 55 inch.

Xét hai tam giác vuông có các cạnh góc vuông là hai cạnh của màn hình hai chiếc ti vi 32 inch và 55 inch. Độ dài đường chéo của chúng lần lượt là 32 inch và 55 inch.

Hai tam giác này đồng dạng với nhau vì có cùng tỉ lệ giữa hai kích thước màn hình.

Suy ra $\frac{x}{72}=\frac{55}{32}$ hay x = 123,75 cm > 1m

Vậy khoảng trống hình vuông cạnh 1 m sẽ không để vừa chiếc ti vi 55 inch.

Giải Toán 8 Kết nối tri thức Tập 2 trang 102, 103

Bài 9.23

Điều kiện nào dưới đây chứng tỏ hai tam giác vuông đồng dạng

a) Một góc nhọn của tam giác này bằng một góc nhọn của tam giác kia

b) Cạnh góc vuông và cạnh huyền của tam giác này tỉ lệ với cạnh góc vuông và cạnh huyền của tam giác kia

c) Một cạnh góc vuông của tam giác này bằng một cạnh góc vuông của tam giác kia

d) Hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia

Lời giải:

Bài 9.24

Cặp tam giác vuông nào đồng dạng với nhau trong hình 9.55.

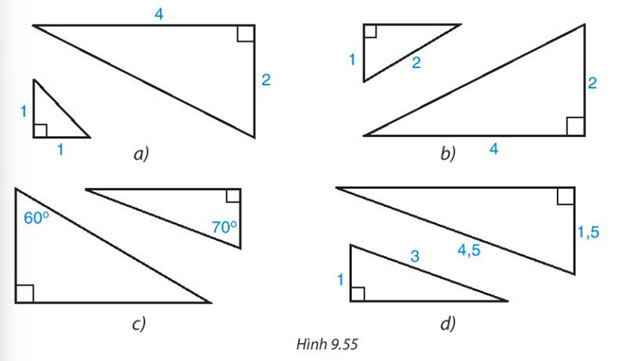
Lời giải:

Bài 9.25

Cho góc nhọn xOy, các điểm A, N nằm trên tia Ox, các điểm B, M nằm trên tia Oy sao cho AM, BN lần lượt vuông góc với Oy, Ox. Chứng minh tam giác OAM đồng dạng với tam giác OBN

Lời giải:

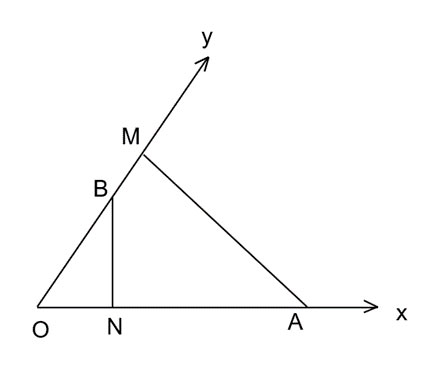
- Xét tam giác OBN có $\widehat{BON}+\widehat{ONB}+\widehat{NBO}$=$180$°

- Xét tam giác MOA có $\widehat{MOA}+\widehat{OMA}+\widehat{OMA}$=$180$°

mà $\widehat{ONB}=\widehat{OMA}=90°$

góc O chung

=> $\widehat{NBO}=\widehat{OMA}$

- Xét hai tam giác vuông OBN (vuông tại N) và tam giác OAM (vuông tại M) có: $\widehat{NBO}=\widehat{OMA}$

=> ΔOAM ~ ΔOBN

Bài 9.26

Cho hai hình chữ nhật ABCD và A'B'C'D' thỏa mãn $AC=3AB$, $B^{\prime }{D}^{\prime }=3A^{\prime }{B}^{\prime }$

a) Chứng minh rằng tam giác ABC đồng dạng với tam giác A'B'C'

b) Nếu A'B' = 2AB và diện tích hình chữ nhật ABCD là $2m^2$ thì diện tích hình chữ nhật A'B'C'D' là bao nhiêu

Lời giải:

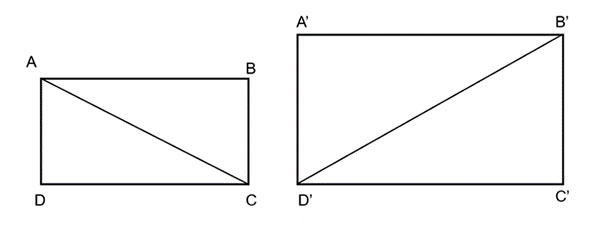
a) Có $AC=3AB$ => $\frac{AB}{AC}=\frac{1}{3}$

- Có $B^{\prime }{D}^{\prime }=3A^{\prime }{B}^{\prime }$ => $\frac{A^{\prime }{B}^{\prime }}{B^{\prime }{D}^{\prime }}=\frac{1}{3}$

=> $\frac{AB}{A^{\prime }{B}^{\prime }}=\frac{AC}{B^{\prime }{D}^{\prime }}$

Xét tam giác vuông ABC (vuông tại A) và tam giác vuông A'B'D' (vuông tại C) có

=> $\frac{AB}{A^{\prime }{B}^{\prime }}=\frac{AC}{B^{\prime }{D}^{\prime }}$

=> $\Delta ABC\Delta C^{\prime }{D}^{\prime }{B}^{\prime }$ (1)

- Xét $\Delta C^{\prime }{D}^{\prime }{B}^{\prime }$ và $\Delta A^{\prime }{B}^{\prime }{C}^{\prime }$

Có B'C' chung, $A^{\prime }{B}^{\prime }=C^{\prime }{D}^{\prime }$, $A^{\prime }{C}^{\prime }=B^{\prime }{D}^{\prime }$ (hai hình chéo của chữ nhật)

=> $\Delta C^{\prime }{D}^{\prime }{B}^{\prime }=\Delta A^{\prime }{B}^{\prime }{C}^{\prime }$ (2)

Từ (1) và (2) chung =>$\Delta ABC\Delta A^{\prime }{B}^{\prime }{C}^{\prime }$

b) - Vì $A^{\prime }{B}^{\prime }=2AB$ => $\frac{AB}{A^{\prime }{B}^{\prime }}=\frac{1}{2}$

mà ΔABC ~ ΔA'B'C' => $\frac{AB}{A^{\prime }{B}^{\prime }}=\frac{AC}{A^{\prime }{C}^{\prime }}=\frac{BC}{B^{\prime }{C}^{\prime }}=\frac{1}{2}$

- Có diện tích ABCD là: $AB.BC$

Có diện tích A'B'C'D' là: $A^{\prime }{B}^{\prime }.B^{\prime }{C}^{\prime }$

=> Xét tỉ lệ hai tam giác ABCD và A'B'C'D', có

$\frac{AB.BC}{A^{\prime }{B}^{\prime }.B^{\prime }{C}^{\prime }}=\frac{AB}{A^{\prime }{B}^{\prime }}\cdot \frac{BC}{B^{\prime }{C}^{\prime }}=\frac{1}{4}$

=> $S_{A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }}=4S_{ABCD}$

mà $S_{ABCD}=2m^2$ => $S_{A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }}=8m^2$

Bài 9.27

Cho tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k. Gọi A'H' và AH lần lượt là các đường cao đỉnh A' và A của tam giác A'B'C' và tam giác ABC. Chứng minh rằng:

a)$\frac{A^{\prime }{H}^{\prime }}{AH}=k$

b) Diện tích tam giác A'B'C' bằng $k^2$ lần diện tích tam giác ABC

Lời giải:

a) Vì $\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }$ ~ $\mathrm{\Delta }ABC$

=> $\hat{B}=\widehat{B^{\prime }}$; $\frac{A^{\prime }{B}^{\prime }}{AB}=\frac{A^{\prime }{C}^{\prime }}{AC}=\frac{B^{\prime }{C}^{\prime }}{BC}=k$

Xét hai tam giác vuông A'H'B' (vuông tại H') và tam giác vuông AHB (vuông tại H), có:

$\hat{B}=\widehat{B^{\prime }}$

=> $\mathrm{\Delta }{A}^{\prime }{H}^{\prime }{B}^{\prime }$ ~ $\mathrm{\Delta }AHB$

=> $\frac{A^{\prime }{H}^{\prime }}{AH}=\frac{A^{\prime }{B}^{\prime }}{AB}$

mà $\frac{A^{\prime }{B}^{\prime }}{AB}=k$

=> $\frac{A^{\prime }{H}^{\prime }}{AH}=k$

b) Có diện tích tam giác ABC là: $\frac{1}{2}AH.BC$

Có diện tích tam giác A'B'C' là $\frac{1}{2}{A}^{\prime }{H}^{\prime }.B^{\prime }{C}^{\prime }$

Xét tỉ lệ giữa hai tam giác A'B'C' và tam giác ABC có: $\frac{\frac{1}{2}{A}^{\prime }{H}^{\prime }.B^{\prime }{C}^{\prime }}{\frac{1}{2}AH.BC}=\frac{A^{\prime }{H}^{\prime }}{AH}\cdot \frac{B^{\prime }{C}^{\prime }}{BC}=k.k=k^2$

Bài 9.28

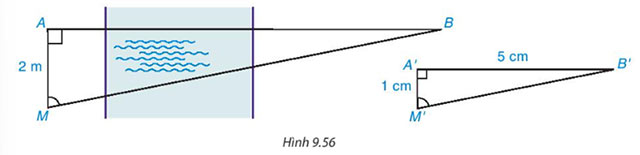
Một người ở vị trí điểm A muốn đo khoảng cách đến điểm B ở bên kia sông mà không thể qua sông được. Sử dụng giác kế, người đó xác định được một điểm M trên bờ sông sao cho AM = 2 m, AM vuông góc với AB và đo được số đo góc AMB. Tiếp theo, người đó vẽ trên giấy tam giác A'M'B' vuông tại A' có AM' = 1cm, $\widehat{A^{\prime }{M}^{\prime }{B}^{\prime }}=\widehat{AMB}$ và đo được A'B' = 5 cm (H.9.56). Hỏi khoảng cách từ A đến B là bao nhiêu mét?

Lời giải:

- Xét $\mathrm{\Delta }{A}^{\prime }{M}^{\prime }{B}^{\prime }$ (vuông tại A) và $\mathrm{\Delta }AMB$ (vuông tại A') có $\widehat{A^{\prime }{M}^{\prime }{B}^{\prime }}=\widehat{AMB}$

=> $\mathrm{\Delta }{A}^{\prime }{M}^{\prime }{B}^{\prime }$ ~ $\mathrm{\Delta }AMB$

=> $\frac{A^{\prime }{M}^{\prime }}{AM}=\frac{A^{\prime }{B}^{\prime }}{AB}$

=> $\frac{1}{2}=\frac{5}{AB}$

=> $AB=10$ (cm)