Toán 8 Bài 38: Hình chóp tam giác đều Giải Toán 8 Kết nối tri thức tập 2 trang 112, 113, 114, 115, 116

Bài trước

Mục lục

Bài sau

Toán 8 Bài 38: Hình chóp tam giác đều là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Kết nối tri thức với cuộc sống tập 2 trang 112, 113, 114, 115, 116.

Giải Toán 8 Kết nối tri thức tập 2 trang 112 → 116 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 38 Chương X: Một số hình khối trong thực tiễn. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Toán 8 Bài 38: Hình chóp tam giác đều Kết nối tri thức

Giải Toán 8 Kết nối tri thức Tập 2 trang 116

Giải Toán 8 Kết nối tri thức Tập 2 trang 116

Bài 10.1

Gọi tên đỉnh, cạnh bên, mặt bên, mặt đáy, đường cao và một trung đoạn của hình chóp tam giác giác đều trong Hình 10.12

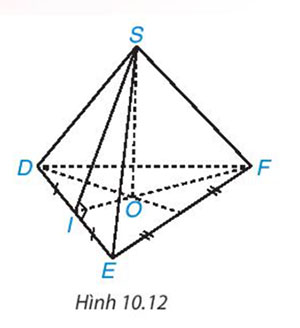
Bài 10.1

Lời giải:

Đỉnh: S
Cạnh bên: SD, SE, SF
Mặt bên: SDE, SEF, SDF
Mặt đáy: DEF
Đường cao: SO
Một trung đoạn: SI

Bài 10.2

Vẽ và cắt một tam giác đều có cạnh 10 cm (H10.13) rồi gấp theo đường màu cam để được hình chóp tam giác đều (H.10.14).

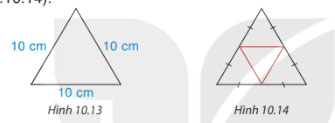
Bài 10.2

Lời giải:

Vẽ và cắt theo yêu cầu của đề bài.

Bài 10.3

Cho hình chóp tam giác đều S.MNP

a) Tính diện tích tam giác MNP

b) Tính thể tích hình chóp S.MNP, biết $\sqrt{27}$ $\sqrt{27}$ ≈ $5,19$

Lời giải:

Vì tam giác MNP đều

=> $MN=NP=MP=6cm$

=> $IN=IP=3cm$

Xét tam giác MIN vuông tại I, có:

$MI^{2}=MN^{2}-IN^{2}=6^{2}-3^{2}$ $MI^{2}=MN^{2}-IN^{2}=6^{2}-3^{2}$

=> $MI$ ≈ $5,2$

=> $S_{MNP}=\frac{1}{2}\cdot MI\cdot NP$ $S_{MNP}=\frac{1}{2}\cdot MI\cdot NP$= $\frac{1}{2}\cdot 5,2\cdot 6$ $\frac{1}{2}\cdot 5,2\cdot 6$ ≈ $15,6$ ( $cm^{2}$ $cm^{2}$)

=> $V=\frac{1}{3}\cdot S\cdot h=\frac{1}{3}\cdot 15,6\cdot 5$ $V=\frac{1}{3}\cdot S\cdot h=\frac{1}{3}\cdot 15,6\cdot 5$ ≈ $26$ ( $cm^{3}$ $cm^{3}$)

Bài 10.4

Nhà bạn Thu có một đèn trang trí có dạng hình chóp tam giác đều. Các cạnh của hình chóp đều bằng nhau và bằng 20 cm. Bạn Thu dự định sẽ dán các mặt bên của đèn bằng những tấm giấy màu. Tính diện tích giấy bạn Thu sử dụng (coi như mép dán không đáng kể). Cho biết $\sqrt{300}$ $\sqrt{300}$ ≈ $17,32$

Lời giải:

- Chiều cao của đèn là: $h=\sqrt{20^{2}-10^{2}}=10\sqrt{3}$ $h=\sqrt{20^{2}-10^{2}}=10\sqrt{3}$ ≈ $17,32$

- Có diện tích của một mặt bên là: $\frac{1}{2}\cdot 17,32\cdot 20=173,2$ $\frac{1}{2}\cdot 17,32\cdot 20=173,2$ ( $cm^{2}$ $cm^{2}$)

=> Diện tích các mặt bên là: $173,2.3=519,6$ ( $cm^{2}$ $cm^{2}$)

Chia sẻ bởi: