Download.vn Học tập Lớp 8 Toán 8 KNTT

Toán 8 Bài tập cuối chương IX Giải Toán 8 Kết nối tri thức tập 2 trang 110, 111

Tải về Bình luận
  • 4
Mục lục

Giải Toán 8 Bài tập cuối chương IX là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Kết nối tri thức với cuộc sống tập 2 trang 110, 111.

Giải bài tập Toán 8 Kết nối tri thức tập 2 trang 110, 111 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài tập cuối chương IX: Tam giác đồng dạng. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Toán 8 Bài tập cuối chương IX Kết nối tri thức

Giải Toán 8 Kết nối tri thức Tập 2 trang 110 - Trắc nghiệm

Bài 9.37

Cho ABC là tam giác không cân. Biết \Delta A'B'C' ~ \Delta ABC. Khẳng định nào sau đây là đúng?

A. \Delta A'C'B' ~ \Delta ACB

B. \Delta B'C'A' ~ \Delta BAC

C. \Delta B'A'C' ~ \Delta BCA

D. \Delta A'C'B' ~ \Delta ABC

Đáp án: A

Bài 9.38

Cho \Delta A'B'C' ~ \Delta ABC với tỉ số đồng dạng bằng 2. Khẳng định nào sau đây là đúng

A. \frac{AB}{A'B'}=2

B. \frac{AB}{A'C'}=2

C. \frac{A'B'}{AB}=2

D. \frac{A'B'}{AC}=2

Đáp án: C

Bài 9.39

Trong các bộ ba số đo dưới đây, đâu là số đo ba cạnh của một tam giác vuông?

A. 3 m; 5 m; 6 m

B. 6 m; 8 m; 10 m

C. 1 cm; 0,5 cm; 1,25 cm

D. 9 m; 16 m; 25 m.

Đáp án: B

Bài 9.40

Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D. Điều nào dưới đây không suy ra \Delta ABC ~ \Delta DEF.

A. \hat{B} =\hat{E}

B. \hat{C} =\hat{F}

C. \hat{B}+\hat{C} =\hat{E} + \hat{F}

D. \hat{B}-\hat{C} =\hat{E} - \hat{F}

Đáp án: D

Giải Toán 8 Kết nối tri thức Tập 2 trang 110, 111 - Tự luận

Bài 9.41

Cho hình 9.73, biết rằng MN // AB, MP // AC. Hãy liệt kê ba cặp hai tam giác (khác nhau) đồng dạng có trong hình

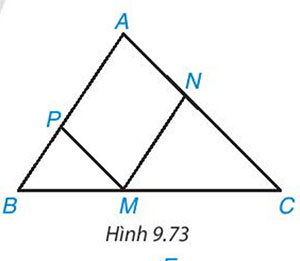
Bài 9.41

Lời giải:

- \Delta CNM ~ \Delta CAB (vì MN // AB) (1)

- \Delta MPB ~ \Delta CAB (vì MP // AC) (2)

- Từ (1) và (2) => \Delta CNM ~ \Delta MPB

Bài 9.42

Cho hình 9.74, biết rằng \widehat{ABD}=\widehat{ACE}. Chứng minh rằng \Delta ABD ~ \Delta ACE và \Delta BOE ~ \Delta COD

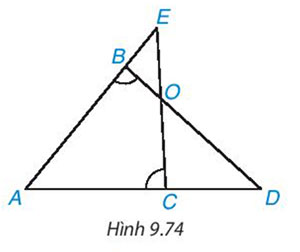
Bài 9.42

Lời giải:

- Xét tam giác ABD và tam giác ACE có \widehat{ABD}=\widehat{ACE}, góc A chung

=> \Delta ABD ~ \Delta ACE (g.g)

- Vì \Delta ABD ~ \Delta ACE

=> \widehat{ADB}=\widehat{AEC}

=> \widehat{CDO}=\widehat{BEO} (1)

- Có \widehat{ABD}=\widehat{ACE}

mà \widehat{ABD}+\widehat{EBO}=180

\widehat{ACE}+\widehat{DCO}=180

=> \widehat{EBO}=\widehat{DCO} (2)

Từ (1) và (2) => \Delta BOE ~ \Delta COD (g.g)

Bài 9.43

Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.75). Chứng minh rằng tam giác GMN đồng dạng với tam giác GBC và tìm tỉ số đồng dạng

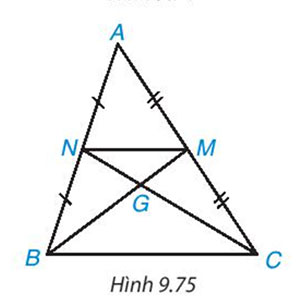
Bài 9.43

Lời giải:

- Xét tam giác ABC có, NA=NB, MA=MC

=> NM là đường trung bình của tam giác ABC

=> NM // BC, NM=\frac{1}{2}AB

- Xét tam giác GMN và tam giác GBC có NM // BC => \Delta GMN ~ \Delta GBC

Bài 9.44

Cho tam giác ABC vuông tại A có AB=5cm, AC=4cm. Gọi AH, HD lần lượt là các đường cao kẻ từ đỉnh A của tam giác ABC và đỉnh H của tam giác HAB

a) Chứng minh rằng \Delta HDA ~ \Delta AHC

b) Tính độ dài các đoạn thẳng HA, HB, HC, HD

Lời giải:

Bài 8.44

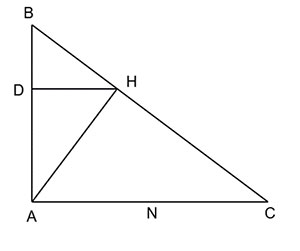
a) Có AB ⊥ AC, HD ⊥ AB

=> HD // AC

=>\widehat{DHA}=\widehat{HAC}

- Xét tam giác vuông HDA (vuông tại D) và tam giác vuông AHC (vuông tại H) có: \widehat{DHA}=\widehat{HAC}

=> \Delta HDA ~ \Delta AHC

b) Xét tam giác ABC có: AB^{2}+AC^{2}=BC^{2}

mà AB=5cm, AC=4cm

=> BC=\sqrt{41}

- Có AH.BC=AB.AC

=> AH=\frac{20\sqrt{41}}{41}

=> HB=AB^{2}-AH^{2} (áp dụng định lý Pythagore trong tam giác vuông BHA)

=> HB=\frac{25\sqrt{41}}{41}

=> HC=\frac{16\sqrt{41}}{41}

- Xét tam giác vuông BDH và tam giác vuông BAC có: HD // AC

=> \Delta BDH ~ \Delta BAC

=> \frac{BH}{BC}=\frac{DH}{AC}

=> HD=\frac{100}{41}

Bài 9.45

Cho tam giác ABC có đường cao AH. Biết AH=12cm, CH=9cm, BH=16cm. Lấy M, N lần lượt là trung điểm của AH, BH

a) Chứng minh rằng ABC là tam giác vuông tại A

b) Chứng minh rằng MN ⊥ AC và CM ⊥ AN

c) Tính diện tích tam giác AMN

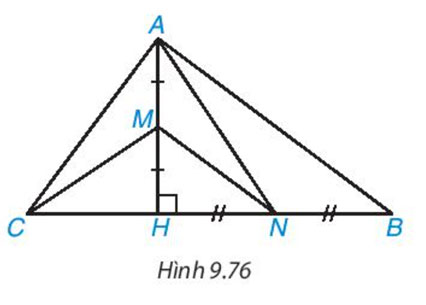
Bài 8.45

Lời giải:

a) Xét tam giác AHB vuông tại H, có:

AH^{2}+HB^{2}=AB^{2} (định lý Pythagore)

=> AB^{2}=12^{2}+16^{2}

=> AB=20cm

Tương tự, có: AC^{2}=AH^{2}+CH^{2} (áp dụng định lý Pythagore trong tam giác vuông AHC)

=> AC^{2}=12^{2}+9^{2}

=> AC=15cm

Có BC=9+16=25

Trong tam giác ABC, nhận thấy AB^{2}+AC^{2}=BC^{2}

=> Tam giác ABC vuông tại A

b) Xét tam giác AHB có:

M là trung điểm của AH

B là trung điểm của BH

=> MN là đường trung bình của tam giác AHB

=> MN // AB

mà AB ⊥ AC (vì tam giác ABC vuông tại A)

=> MN ⊥ AC

Bài 9.46

Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC . Chứng minh rằng:

a)\frac{BD}{BC}=\frac{AB}{AB+AC}, từ đó suy ra AE=\frac{AB.AC}{AB+AC}

b) \Delta DFC ~ \Delta ABC

c) DF=DB

Bài 9.44

Bài 9.47

Để tính được chiều cao gần đúng của kim tự tháp Ai Cập, người ta nắm 1 cây cọc cao 1m vuông góc với mặt đất và đo được bóng cây cọc trên mặt đất là 1,5m. Khi đó chiều dài bóng của kim tự tháp trên mặt đất là 208,2 m. Hỏi kim tự tháp cao bao nhiêu mét?

Bài 9.48

Từ căn hộ chung cư nhà mình, bạn Lan đứng cách cửa sổ 1m nhìn sang tòa nhà đối diện thì vừa nhìn thấy đúng tất cả 6 tầng của tòa nhà đó. Biết rằng cửa sổ nhà Lan cao 80cm và mỗi tầng của tòa nhà đối diện 4m. Hỏi khoảng cách từ căn hộ nhà Lan đến tòa nhà đối diện là bao nhiêu?

Chia sẻ bởi: 👨 Lê Thị tuyết Mai
Mời bạn đánh giá!
  • Lượt tải: 14
  • Lượt xem: 322
  • Dung lượng: 283,3 KB
Liên kết tải về

Link Download chính thức:

Tìm thêm: Toán lớp 8 Toán 8 Giải SGK Toán 8 Kết nối tri thức với cuộc sống
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần

    Toán 8 Kết nối tri thức với cuộc sống