Toán 8 Bài tập cuối chương I Giải Toán 8 Kết nối tri thức trang 27, 28

Mục lục

Giải bài tập Toán lớp 8 Bài tập cuối chương I với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 8 Tập 1 Kết nối tri thức với cuộc sống trang 27, 28. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 8 chi tiết, còn giúp các em hệ thống lại toàn bộ kiến thức trọng tâm của Bài tập cuối chương I: Đa thức. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Toán 8 Bài tập cuối chương I Kết nối tri thức

Phần Trắc nghiệm
Phần Tự luận

Xem thêm

Phần Trắc nghiệm

Bài 1.39 trang 27 Toán 8 tập 1

Đơn thức $-2^{3}x^{2}yz^{3}$ $- 2^{3} x^{2} y z^{3}$ có:

A. hệ số -2, bậc 8

B. hệ số $-2^{3}$ $- 2^{3}$ , bậc 5

C. hệ số -1, bậc 9

D. hệ số $-2^{3}$ $- 2^{3}$ , bậc 6

Lời giải:

- 2³x²yz³:

Hệ số: - 2³

Bậc: 2 + 1 + 3 = 6

=> Đáp án D

Bài 1.40 trang 27 Toán 8 tập 1

Gọi T là tổng, H là hiệu của hai đa thức $3x^{2}y-2xy^{2}+xy$ $3 x^{2} y - 2 x y^{2} + x y$ và $-2x^{2}y+3xy^{2}+1$ $- 2 x^{2} y + 3 x y^{2} + 1$ . Khi đó:

A. $T=x^{2}y-xy^{2}+xy+1$ $T = x^{2} y - x y^{2} + x y + 1$ và $H=5x^{2}y-5xy^{2}+xy-1$ $H = 5 x^{2} y - 5 x y^{2} + x y - 1$

B. $T=x^{2}y+xy^{2}+xy+1$ $T = x^{2} y + x y^{2} + x y + 1$ và $H=5x^{2}y-5xy^{2}+xy-1$ $H = 5 x^{2} y - 5 x y^{2} + x y - 1$

C. $T=x^{2}y+xy^{2}+xy+1$ $T = x^{2} y + x y^{2} + x y + 1$ và $H=5x^{2}y-5xy^{2}-xy-1$ $H = 5 x^{2} y - 5 x y^{2} - x y - 1$

D. $T=x^{2}y+xy^{2}+xy-1$ $T = x^{2} y + x y^{2} + x y - 1$ và $H=5x^{2}y+5xy^{2}+xy-1$ $H = 5 x^{2} y + 5 x y^{2} + x y - 1$

Lời giải:

Đáp án đúng: B

$T = (3 x^{2} y - 2 x y^{2} + x y) + (- 2 x^{2} y + 3 x y^{2} + 1)$

$= 3 x^{2} y - 2 x y^{2} + x y - 2 x^{2} y + 3 x y^{2} + 1$

$=\left(3x^2y-2x^2y\right)+\left(-2xy^2+3xy^2\right)+xy+1$ $= (3 x^{2} y - 2 x^{2} y) + (- 2 x y^{2} + 3 x y^{2}) + x y + 1$

$= x^{2} y + x y^{2} + x y + 1$

$H = (3 x^{2} y - 2 x y^{2} + x y) - (- 2 x^{2} y + 3 x y^{2} + 1)$

$= 3 x^{2} y - 2 x y^{2} + x y + 2 x^{2} y - 3 x y^{2} - 1$

$= (3 x^{2} y + 2 x^{2} y) + (- 2 x y^{2} - 3 x y^{2}) + x y - 1$

$= 5 x^{2} y + (- 5 x y^{2}) + x y - 1$

$= 5 x^{2} y - 5 x y^{2} + x y - 1$

Bài 1.41 trang 27 Toán 8 tập 1

Tích của hai đơn thức $6x^{2}yz$ $6 x^{2} y z$ và $-2y^{2}z^{2}$ $- 2 y^{2} z^{2}$ là đơn thức

A. $4x^{2}y^{3}z^{3}$ $4 x^{2} y^{3} z^{3}$

B. $-12x^{2}y^{3}z^{3}$ $- 12 x^{2} y^{3} z^{3}$

C. $-12x^{3}y^{3}z^{3}$ $- 12 x^{3} y^{3} z^{3}$

D. $4x^{3}y^{3}z^{3}$ $4 x^{3} y^{3} z^{3}$

Lời giải:

6x²yz . (- 2y²z²)

= 6.(- 2)x²(y.y²)(z.z²)

= -12x²y³z³

=> Đáp số đúng: B

Bài 1.42 trang 27 Toán 8 tập 1

Khi chia đa thức $8x^{3}y^{2}-6x^{2}y^{3}$ $8 x^{3} y^{2} - 6 x^{2} y^{3}$ cho đơn thức -2xy, ta được kết quả là

A. $-4x^{2}y+3xy^{2}$ $- 4 x^{2} y + 3 x y^{2}$

B. $-4xy^{2}+3x^{2}y$ $- 4 x y^{2} + 3 x^{2} y$

C. $-10x^{2}y+4xy^{2}$ $- 10 x^{2} y + 4 x y^{2}$

D. $-10x^{2}y+4xy^{2}$ $- 10 x^{2} y + 4 x y^{2}$

Lời giải:

Đáp án đúng: A

(8x³y² - 6x²y³) : (- 2xy)

= 8x³y² : (- 2xy) - 6x²y³ : (- 2xy)

= (- 4x²y) + 3xy²

= - 4x²y + 3xy²

Phần Tự luận

Bài 1.43 trang 27 Toán 8 tập 1

Một đa thức hai biến bậc hai thu gọn có thể có nhiều nhất

a) bao nhiêu hạng tử bậc hai? Cho ví dụ.

b) bao nhiêu hạng tử bậc nhất? Cho ví dụ.

c) bao nhiêu hạng tử khác 0? Cho ví dụ.

Bài giải:

a) Một đa thức hai biến bậc hai thu gọn có thể nhiều nhất 3 hạng tử bậc hai.

VD: $-x^{2}+2y^{2}-7xy +6$ $- x^{2} + 2 y^{2} - 7 x y + 6$ , đa thức này có 3 hạng tử bậc hai là: $-x^{2};2y^{2};-7xy$ $- x^{2}; 2 y^{2}; - 7 x y$

b) Một đa thức hai biến bậc hai thu gọn có thể nhiều nhất 2 hạng tử bậc nhất.

VD: 8xy + 2x + y, đa thức này có 2 hạng tử bậc nhất là: 2x và y

c) Một đa thức hai biến bậc hai thu gọn có thể nhiều nhất 5 hạng tử khác 0

VD: $8x^{2}+4y^{2}-xy -5x + y-1$ $8 x^{2} + 4 y^{2} - x y - 5 x + y - 1$ , đa thức này có 5 hạng tử khác 0 là $8x^{2},4y^{2},-xy,-5x,y$ $8 x^{2}, 4 y^{2}, - x y, - 5 x, y$

Bài 1.44 trang 27 Toán 8 tập 1

Cho biểu thức $$x^{3}(x^{5}-y^{5})+y^{5}(3x^{3}-y^{3})$ $$ x^{3} (x^{5} - y^{5}) + y^{5} (3 x^{3} - y^{3})$

a) Rút gọn biểu thức

b) Tính giá trị của biểu thức đã cho nếu biết $y^{4}=x^{4}\sqrt{3}$ $y^{4} = x^{4} \sqrt{3}$

Bài giải:

a) $3x^{3}(x^{5}-y^{5})+y^{5}(3x^{3}-y^{3})$ $3 x^{3} (x^{5} - y^{5}) + y^{5} (3 x^{3} - y^{3})$

$=3x^{8}-3x^{3}y^{5}+3x^{3}y^{5}-y^{8}=3x^{8}-y^{8}$ $= 3 x^{8} - 3 x^{3} y^{5} + 3 x^{3} y^{5} - y^{8} = 3 x^{8} - y^{8}$

b) $3x^{8}-y^{8}=(x^{4}\sqrt{3})^{2}-(y^{4})^{2}$ $3 x^{8} - y^{8} = (x^{4} \sqrt{3})^{2} - (y^{4})^{2}$

$=(x^{4}\sqrt{3}-y^{4})\times (x^{4}\sqrt{3}+y^{4})=0$ $= (x^{4} \sqrt{3} - y^{4}) \times (x^{4} \sqrt{3} + y^{4}) = 0$

Bài 1.45 trang 28 Toán 8 tập 1

Rút gọn biểu thức

$\frac{1}{4}(2x^{2}+y)(x-2y^{2})+\frac{1}{4}(2x^{2}-y)(x+2y^{2})$ $\frac{1}{4} (2 x^{2} + y) (x - 2 y^{2}) + \frac{1}{4} (2 x^{2} - y) (x + 2 y^{2})$

Bài giải:

$\frac{1}{4}(2x^{2}+y)(x-2y^{2})+\frac{1}{4}(2x^{2}-y)(x+2y^{2})$ $\frac{1}{4} (2 x^{2} + y) (x - 2 y^{2}) + \frac{1}{4} (2 x^{2} - y) (x + 2 y^{2})$

$=\frac{1}{4}(2x^{3}-4x^{2}y^{2}+xy-2y^{3})+\frac{1}{4}(2x^{3}+4x^{2}y^{2}-xy-2y^{3})$ $= \frac{1}{4} (2 x^{3} - 4 x^{2} y^{2} + x y - 2 y^{3}) + \frac{1}{4} (2 x^{3} + 4 x^{2} y^{2} - x y - 2 y^{3})$

$=\frac{1}{4}(2x^{3}-4x^{2}y^{2}+xy-2y^{3}+2x^{3}+4x^{2}y^{2}-xy-2y^{3})$ $= \frac{1}{4} (2 x^{3} - 4 x^{2} y^{2} + x y - 2 y^{3} + 2 x^{3} + 4 x^{2} y^{2} - x y - 2 y^{3})$

$=\frac{1}{4}(4x^{3}-4y^{3})=x^{3}-y^{3}$ $= \frac{1}{4} (4 x^{3} - 4 y^{3}) = x^{3} - y^{3}$

Bài 1.46 trang 28 Toán 8 tập 1

Bạn Thành dùng một miếng bìa hình chữ nhật để làm một chiếc hộp (không nắp) bằng cách cắt bốn hình vuông cạnh x cm ở bốn góc (H.1.3) rồi gấp lại. Biết rằng miếng bìa có chiều dài là y cm, chiều rộng là z cm

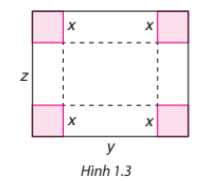
Bài 1.46

Tìm đa thức (ba biến x, y, z) biểu thị thể tích của chiếc hộp. Xác định bậc của đa thức đó

Bài giải:

Chiều cao của chiếc hộp là x

Chiều dài của đáy hộp là y - 2x

Chiều rộng của đáy hộp là z - 2x

Thể tích của chiếc hộp là: $x\times (y-2x)\times (z-2x)=xyz-2x^{2}y-2x^{2}z+4x^{3}$ $x \times (y - 2 x) \times (z - 2 x) = x y z - 2 x^{2} y - 2 x^{2} z + 4 x^{3}$

Đa thức bậc 3

Bài 1.47 trang 28 Toán 8 tập 1

Biết rằng D là một đơn thức sao cho $-2x^{3}y^{4}:D=xy^{2}$ $- 2 x^{3} y^{4} : D = x y^{2}$ . Hãy tìm thương của phép chia:

$(10x^{5}y^{2}-6x^{3}y^{4}+8x^{2}y^{5}):D$ $(10 x^{5} y^{2} - 6 x^{3} y^{4} + 8 x^{2} y^{5}) : D$

Bài giải:

$-2x^{3}y^{4}:D=xy^{2}$ $- 2 x^{3} y^{4} : D = x y^{2}$

$\Rightarrow D= -2x^{3}y^{4}:xy^{2}=-2x^{2}y^{2}$ $\Rightarrow D = - 2 x^{3} y^{4} : x y^{2} = - 2 x^{2} y^{2}$

$(10x^{5}y^{2}-6x^{3}y^{4}+8x^{2}y^{5}):D=(10x^{5}y^{2}-6x^{3}y^{4}+8x^{2}y^{5}):(-2x^{2}y^{2})$ $(10 x^{5} y^{2} - 6 x^{3} y^{4} + 8 x^{2} y^{5}) : D = (10 x^{5} y^{2} - 6 x^{3} y^{4} + 8 x^{2} y^{5}) : (- 2 x^{2} y^{2})$

$=-5x^{3}+3xy^{2}-4y^{3}$ $= - 5 x^{3} + 3 x y^{2} - 4 y^{3}$

Bài 1.48 trang 28 Toán 8 tập 1

Làm phép chia sau theo hướng dẫn:

$[8x^{3}(2x-5)^{2}-6x^{2}(2x-5)^{3}+10x(2x-5)^{2}]:2x(2x-5)^{2}$ $[8 x^{3} (2 x - 5)^{2} - 6 x^{2} (2 x - 5)^{3} + 10 x (2 x - 5)^{2}] : 2 x (2 x - 5)^{2}$

Hướng dẫn: Đặt y = 2x - 5

Bài giải:

$[8x^{3}(2x-5)^{2}-6x^{2}(2x-5)^{3}+10x(2x-5)^{2}]:2x(2x-5)^{2}$ $[8 x^{3} (2 x - 5)^{2} - 6 x^{2} (2 x - 5)^{3} + 10 x (2 x - 5)^{2}] : 2 x (2 x - 5)^{2}$

Đặt y = 2x - 5, ta có:

$[8x^{3}y^{2}-6x^{2}y^{3}+10xy^{2}]:2xy^{2}$ $[8 x^{3} y^{2} - 6 x^{2} y^{3} + 10 x y^{2}] : 2 x y^{2}$

$=4x^{2}-3xy+5$ $= 4 x^{2} - 3 x y + 5$

$=4x^{2}-3x(2x-5)+5=4x^{2}-6x^{2}+15x+5$ $= 4 x^{2} - 3 x (2 x - 5) + 5 = 4 x^{2} - 6 x^{2} + 15 x + 5$

$=-2x^{2}+15x+5$ $= - 2 x^{2} + 15 x + 5$

Chia sẻ bởi:

Lê Thị tuyết Mai

Tải về

Bài trước

Luyện tập chung trang 25

Bài sau

Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu

Liên kết tải về

Toán 8 Bài tập cuối chương I 230,3 KB Tải về

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!