Download.vn Học tập Lớp 8 Toán 8 KNTT

Toán 8 Bài 9: Phân tích đa thức thành nhân tử Giải Toán 8 Kết nối tri thức trang 42, 43, 44

Tải về Bình luận
  • 2
Mục lục

Toán 8 Bài 9: Phân tích đa thức thành nhân tử là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Kết nối tri thức với cuộc sống tập 1 trang 42, 43, 44.

Giải Toán 8 Kết nối tri thức tập 1 trang 42 → 44 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 9 Chương II: Hằng đẳng thức đáng nhớ và ứng dụng. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Toán 8 Bài 9: Phân tích đa thức thành nhân tử Kết nối tri thức

Giải Toán 8 Kết nối tri thức Tập 1 trang 44

Bài 2.22

Phân tích các đa thức sau thành nhân tử:

a) x^{2}+xy

b) 6a^{2}b-18ab

c) x^{3}-4x

d) x^{4}-8x

Bài giải:

a) x^{2}+xy=x(x+y)

b) 6a^{2}b-18ab=6ab(a-3)

c) x^{3}-4x=x(x^{2}-4)=x(x+2)(x-2)

d) x^{4}-8x=x(x^{3}-8)=x(x-2)(x^{2}+2x+4)

Bài 2.23

Phân tích các đa thức sau thành nhân tử

a) x^{2}-9+xy+3y

b) x^{2}y+x^{2}+xy-1

Bài giải:

a) x^{2}-9+xy+3y=(x^{2}-9)+(xy+3y)

=(x+3)(x-3)+y(x+3)=(x+3)(x-3+y)

b) x^{2}y+x^{2}+xy-1=(x^{2}y+xy)+(x^{2}-1)

=xy(x+1)+(x-1)(x+1)=(x+1)(xy+x-1)

Bài 2.24

Tìm x, biết:

a) x^{2}-4x=0

b) 2x^{3}-2x=0

Bài giải:

a) x^{2}-4x=0

\Rightarrow x(x-4)=0

\Rightarrow x=0 hoặc x - 4 = 0

\Rightarrow x=0 hoặc x = 4

b) 2x^{3}-2x=0

\Rightarrow 2x(x-1)=0

\Rightarrow 2x=0 hoặc x - 1 = 0

\Rightarrow x=0 hoặc x = 1

Bài 2.25

Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng y (mét) (H.2.2)

a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y

b) Phân tích S thành nhân tử rồi tính S khi x = 102, y = 2 m

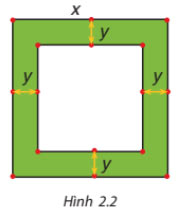
Bài 2.25

Bài giải:

a) S=x^{2}-y^{2}(m^{2})

b) S=x^{2}-y^{2}=(x-y)(x+y)

Thay x = 102m, y =2 m vào S ta có:

S = (102 - 2)(102 + 2) = 100 x 104 = 10400 (m2)

Chia sẻ bởi: 👨 Lê Thị tuyết Mai
Mời bạn đánh giá!
  • Lượt tải: 13
  • Lượt xem: 603
Liên kết tải về

Link Download chính thức:

Tìm thêm: Toán lớp 8 Toán 8 Giải SGK Toán 8 Kết nối tri thức với cuộc sống
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần

    Toán 8 Kết nối tri thức với cuộc sống