Toán 7 Bài tập cuối chương IV - Kết nối tri thức với cuộc sống Giải Toán lớp 7 trang 87 - Tập 1

Bài trước

Mục lục

Bài sau

Giải bài tập Toán lớp 7 Bài tập cuối chương IV với lời giải chi tiết, rõ ràng theo khung chương trình SGK Toán 7 Tập 1 Kết nối tri thức với cuộc sống trang 87. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 7 chi tiết, còn giúp các em hệ thống lại toàn bộ kiến thức trọng tâm của Bài tập cuối chương IV: Tam giác bằng nhau. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 7 Bài tập cuối chương IV sách Kết nối tri thức với cuộc sống

Giải Toán 7 Kết nối tri thức với cuộc sống trang 87 tập 1

Giải Toán 7 Kết nối tri thức với cuộc sống trang 87 tập 1

Bài 4.33

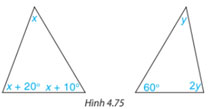
Tính các số đo x, y trong tam giác dưới đây (H.4.75)

H.4.75

Hướng dẫn giải:

Các trường hợp bằng nhau của tam giác:

+ Trường hợp 1: cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

+ Trường hợp 2: cạnh – góc – cạnh: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

+ Trường hợp 3: góc – cạnh – góc: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Gợi ý đáp án:

Áp dụng định lí tổng ba góc trong tam giác,

+) Ta có:

$\begin{array}{l}x + x + {20^o} + x + {10^o} = {180^o}\\ \Rightarrow 3x = {150^o}\\ \Rightarrow x = {50^o}\end{array}$ $\begin{array}{l}x + x + {20^o} + x + {10^o} = {180^o}\\ \Rightarrow 3x = {150^o}\\ \Rightarrow x = {50^o}\end{array}$

+) Ta có:

$\begin{array}{l}y + {60^o} + 2y = {180^o}\\ \Rightarrow 3y = {120^o}\\ \Rightarrow y = {40^o}\end{array}$ $\begin{array}{l}y + {60^o} + 2y = {180^o}\\ \Rightarrow 3y = {120^o}\\ \Rightarrow y = {40^o}\end{array}$

Bài 4.34

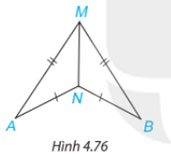
Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh rằng $\widehat {MAN} = \widehat {MBN}$ $\widehat {MAN} = \widehat {MBN}$.

Hình 4.76

Hướng dẫn giải:

- Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau (cùng bằng 60⁰)

- Tam giác cân có một góc bằng 60⁰ là tam giác đều.

- Điểm nằm trên đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

Gợi ý đáp án:

Xét 2 tam giác MNA và MNB có:

AM=BM

AN=BN

MN chung

$=>\Delta MNA = \Delta MNB (c.c.c)$ $=>\Delta MNA = \Delta MNB (c.c.c)$

$=>\widehat {MAN} = \widehat {MBN}$ $=>\widehat {MAN} = \widehat {MBN}$ (2 góc tương ứng)

Bài 4.35

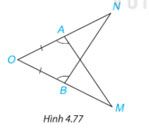
Trong Hình 4.77, có $AO = BO,\widehat {OAM} = \widehat {OBN}$ $AO = BO,\widehat {OAM} = \widehat {OBN}$. Chứng minh rằng AM = BN.

Hình 4.77

Hướng dẫn giải:

Các trường hợp bằng nhau của tam giác:

+ Trường hợp 1: cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

+ Trường hợp 3: góc – cạnh – góc: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Gợi ý đáp án:

Xét 2 tam giác OAM và OBN có:

$\widehat {OAM} = \widehat {OBN}$ $\widehat {OAM} = \widehat {OBN}$

AO=BO

Góc O chung

$=>\Delta OAM = \Delta OBN(g.c.g)$ $=>\Delta OAM = \Delta OBN(g.c.g)$

=>AM=BN (2 cạnh tương ứng)

Bài 4.36

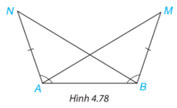
Trong Hình 4.78, ta có $AN = BM,\widehat {BAN} = \widehat {ABM}$ $AN = BM,\widehat {BAN} = \widehat {ABM}$. Chứng minh rằng $\widehat {BAM} = \widehat {ABN}$ $\widehat {BAM} = \widehat {ABN}$.

Hình 4.78

Hướng dẫn giải:

Các trường hợp bằng nhau của tam giác:

+ Trường hợp 1: cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

+ Trường hợp 3: góc – cạnh – góc: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Gợi ý đáp án:

Xét 2 tam giác ANB và BMA có:

AN=BM

$\widehat {BAN} = \widehat {ABM}$ $\widehat {BAN} = \widehat {ABM}$

AB chung

$=>\Delta ANB = \Delta BMA(c.g.c)$ $=>\Delta ANB = \Delta BMA(c.g.c)$

Bài 4.37

Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Theo em, tứ giác AMBN là hình gì?

Hướng dẫn giải:

- Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau (cùng bằng 60⁰)

- Tam giác cân có một góc bằng 60⁰ là tam giác đều.

- Điểm nằm trên đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

Gợi ý đáp án:

Hình vẽ minh họa:

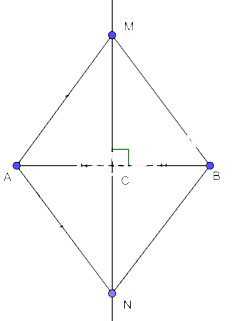
Bài 4.37

Ta có: M thuộc đường trung thực của đoạn thẳng AB

=> MA = MB (tính chất đường trung trực) (1)

N thuộc đường trung thực của đoạn thẳng AB

=> NA = NB (tính chất đường trung trực) (2)

Mà AM = AN (3)

Từ (1), (2) và (3)

=> AM = MB = BN = NA

=> AMBN là hình thoi

Bài 4.38

Cho tam giác ABC cân tại A có $\widehat {A{\rm{ }}} = 120^\circ$ $\widehat {A{\rm{ }}} = 120^\circ$. Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:

a) $\Delta BAM = \Delta CAN$ $\Delta BAM = \Delta CAN$;

b) Các tam giác ANB, AMC lần lượt cân tại N, M.

Hướng dẫn giải:

- Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau (cùng bằng 60⁰)

- Tam giác cân có một góc bằng 60⁰ là tam giác đều.

- Điểm nằm trên đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

Gợi ý đáp án:

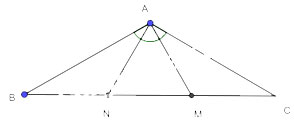
Bài 4.38

a) Xét tam giác ABM vuông tại A và tam giác CAN vuông tại N ta có:

AB = AC (tam giác ABC cân)

$\widehat {ABN} = \widehat {ACM}$ $\widehat {ABN} = \widehat {ACM}$ (tam giác ABC cân tại A)

=> ∆ABM = ∆CAN

b) Xét tam giác ABC cân tại A ta có:

$\widehat B = \widehat C$ $\widehat B = \widehat C$

$\widehat A + \widehat B + \widehat C = {180^0}$ $\widehat A + \widehat B + \widehat C = {180^0}$

=> $\widehat B = \widehat C = \frac{{{{180}^0} - \widehat A}}{2} = \frac{{{{180}^0} - {{120}^0}}}{2} = {30^0}$ $\widehat B = \widehat C = \frac{{{{180}^0} - \widehat A}}{2} = \frac{{{{180}^0} - {{120}^0}}}{2} = {30^0}$

Ta có:

$\begin{matrix} \widehat A = {120^0} \hfill \\ \Rightarrow \widehat {BAM} + \widehat {MAC} = {120^0} \hfill \\ \Rightarrow \widehat {MAC} = {120^0} - \widehat {BAM} = {120^0} - {90^0} = {30^0} \hfill \\ \end{matrix}$ $\begin{matrix} \widehat A = {120^0} \hfill \\ \Rightarrow \widehat {BAM} + \widehat {MAC} = {120^0} \hfill \\ \Rightarrow \widehat {MAC} = {120^0} - \widehat {BAM} = {120^0} - {90^0} = {30^0} \hfill \\ \end{matrix}$

Tương tự:

$\begin{matrix} \widehat {NAC} + \widehat {BAN} = {120^0} \hfill \\ \Rightarrow \widehat {BAN} = {120^0} - \widehat {NAC} = {120^0} - {90^0} = {30^0} \hfill \\ \end{matrix}$ $\begin{matrix} \widehat {NAC} + \widehat {BAN} = {120^0} \hfill \\ \Rightarrow \widehat {BAN} = {120^0} - \widehat {NAC} = {120^0} - {90^0} = {30^0} \hfill \\ \end{matrix}$

Xét tam giác ABN có:

$\widehat {ABN} = \widehat {NAB} = {30^0}$ $\widehat {ABN} = \widehat {NAB} = {30^0}$

=> Tam giác ABN cân tại N

Xét tam giác ACM có:

$\widehat {MAC} = \widehat {MCA} = {30^0}$ $\widehat {MAC} = \widehat {MCA} = {30^0}$

=> Tam giác ACM cân tại M

Bài 4.39

Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho $\widehat {CAM} = {30^o}$ $\widehat {CAM} = {30^o}$. Chứng minh rằng:

a) Tam giác CAM cân tại M;

b) Tam giác BAM là tam giác đều;

c) M là trung điểm của đoạn thẳng BC.

Hướng dẫn giải:

- Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau (cùng bằng 60⁰)

- Tam giác cân có một góc bằng 60⁰ là tam giác đều.

- Điểm nằm trên đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

Gợi ý đáp án:

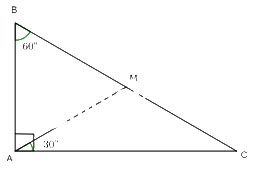
Bài 4.39

a) Xét tam giác ABC có:

$\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ = > {90^o} + {60^o} + \widehat C = {180^o}\\ = > \widehat C = {30^o}\end{array}$ $\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ = > {90^o} + {60^o} + \widehat C = {180^o}\\ = > \widehat C = {30^o}\end{array}$

Xét tam giác CAM có $\widehat A = \widehat C = {30^o}$ $\widehat A = \widehat C = {30^o}$

=>Tam giác CAM cân tại M.

b) Xét tam giác ABM có:

$\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ = > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ = > \widehat {CMA} = {120^o}\\ = > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}$ $\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ = > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ = > \widehat {CMA} = {120^o}\\ = > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}$

Xét tam giác ABM có:

$\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ = > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ = > \widehat {BAM} = {60^o}\end{array}$ $\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ = > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ = > \widehat {BAM} = {60^o}\end{array}$

Do $\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}$ $\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}$ nên tam giác ABM đều.

c) Vì ΔABM đều nên AB = BM = AM

Mà ΔCAM cân tại M nên MA = MC

Do đó, MB = MC. Mà M nằm giữa B và C

=> M là trung điểm của BC.

Chia sẻ bởi: