Toán 7 Luyện tập chung trang 74 Giải Toán lớp 7 trang 74 sách Kết nối tri thức - Tập 1

Giải bài tập Toán lớp 7 Luyện tập chung với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 7 Tập 1 Kết nối tri thức với cuộc sống trang 74. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 7 chi tiết, còn giúp các em hệ thống lại toàn bộ kiến thức trọng tâm của Luyện tập chung Chương IV: Tam giác bằng nhau. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 7 Kết nối tri thức với cuộc sống trang 74 tập 1

Bài 4.16

Cho hai tam giác ABC và DEF thoả mãn \(AB = DE,AC = DF,\widehat {BAC} = \widehat {EDF} = {60^\circ },BC = 6\;{\rm{cm}},\widehat {ABC} = {45^\circ }\). Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.

Hướng dẫn giải

Trường hợp bằng nhau cạnh – góc - cạnh (c – g – c)

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

Trường hợp bằng nhau góc – cạnh – góc (g – c – g)

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Gợi ý đáp án:

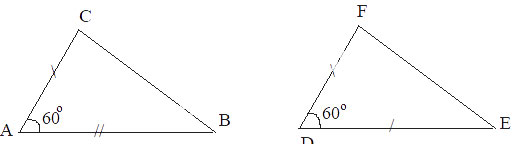
Xét hai tam giác ABC và DEF có:

\(\begin{array}{l}AB = DE\\AC = DF\\\widehat {BAC} = \widehat {EDF} = {60^\circ }\end{array}\)

\(\Rightarrow \Delta ABC = \Delta DEF(c.g.c)\)

Do đó:

EF = BC = 6cm

\(\widehat {DEF} = \widehat {ABC} = {45^o}\)

\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\\ \Rightarrow {60^o} + {45^o} + \widehat {ACB} = {180^o}\\ \Rightarrow \widehat {ACB} = {75^o}\end{array}\)

\(\Rightarrow \widehat {EFD} = \widehat {ACB} = {75^o}\)

Bài 4.17

Cho hai tam giác ABC và DEF thoả mãn \(AB = DE, \widehat {ABC} = \widehat {DEF} = {70^\circ },\widehat {BAC} = \widehat {EDF} = {60^\circ },AC = 6\;{\rm{cm}}\).

Tính độ dài cạnh DF.

Hướng dẫn giải

Trường hợp bằng nhau cạnh – góc - cạnh (c – g – c)

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

Trường hợp bằng nhau góc – cạnh – góc (g – c – g)

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Gợi ý đáp án:

Hình vẽ minh họa

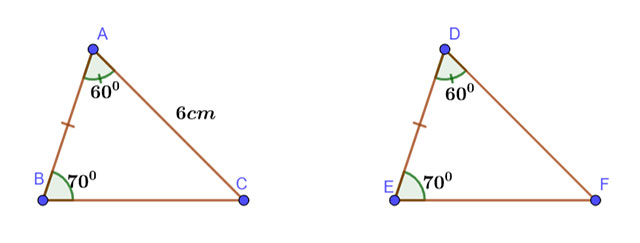
Xét tam giác ABC và tam giác DEF ta có:

AB = DE

\(\widehat {ABC} = \widehat {DEF} = {70^0}\)(giả thiết)

\(\widehat {BAC} = \widehat {EDF} = {60^0}\)(giả thiết)

=> ∆ABC = ∆DEF

=> AC = DF = 6 cm (Hai cạnh tương ứng)

Bài 4.18

Cho Hình 4.44, biết EC = ED và \(\widehat {AEC} = \widehat {AED}\). Chứng minh rằng:

\(\begin{array}{*{20}{l}}{{\rm{ a) }}\Delta AEC = \Delta AED;}&{{\rm{ b) }}\Delta ABC = \Delta ABD.}\end{array}\)

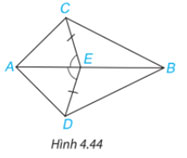
Hướng dẫn giải:

Trường hợp bằng nhau cạnh – góc - cạnh (c – g – c)

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

Trường hợp bằng nhau góc – cạnh – góc (g – c – g)

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Gợi ý đáp án:

a) Xét hai tam giác AEC và AED có

EC = ED

\(\widehat {CEA} = \widehat {DEA}\)

AE chung

\(\Rightarrow \Delta AEC{\rm{ = }}\Delta AED(c.g.c)\)

b) Do \(\Delta AEC{\rm{ = }}\Delta AED\) nên \(\widehat {CAE} = \widehat {DAE}\) (2 góc tương ứng) và AC=AD (2 cạnh tương ứng).

Xét \(\Delta ABC\) và \(\Delta ABD\) có:

AB chung

\(\widehat {CAE} = \widehat {DAE}\)

AC=AD

\(\Rightarrow \Delta ABC = \Delta ABD(c.g.c)\)

Bài 4.19

Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz sao cho \(\widehat {CAO} = \widehat {CBO}\).

a) Chứng minh rằng \(\Delta OAC = \Delta OBC\).

b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng \(\Delta MAC = \Delta MBC\).

Phương pháp giải:

a) Chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.

b) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc - cạnh.

Gợi ý đáp án:

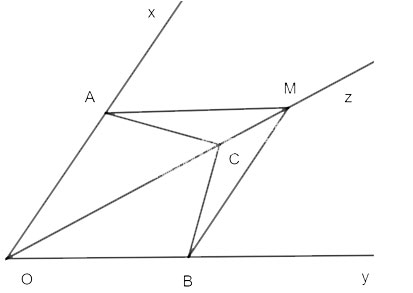
a) Xét \(\Delta OAC\) và \(\Delta OBC\) có:

\(\widehat {AOC} = \widehat {AOB}\)(Oz là phân giác góc xOy)

OC chung

\(\widehat {CAO} = \widehat {CBO}\)

\(\Rightarrow \Delta OAC = \Delta OBC(g.c.g)\)

b) Do \(\Delta OAC = \Delta OBC\) nên AC=BC (2 cạnh tương ứng)

Vì \(\widehat {ACO}\) và \(\widehat {ACM}\) kề bù

\(\widehat {BCO}\) và \(\widehat {BCM}\) kề bù

Mà \(\widehat {ACO} = \widehat {BCO}\) nên \(\widehat {ACM} = \widehat {BCM}\)

Xét \(\Delta MAC\) và \(\Delta MBC\) có:

AC=BC

\(\widehat {ACM} = \widehat {BCM}\)

CM chung

\(\Rightarrow \Delta MAC = \Delta MBC(c.g.c)\)

Lý thuyết Luyện tập chung trang 74

1. Hai tam giác bằng nhau

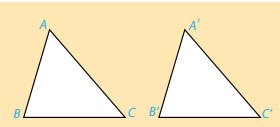
Hai tam giác ABC và A’B’C’ bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau, tức là:

AB = A’B’ ; AC = A’C’ ; BC = B’C’ và  \(\widehat {A} = \widehat {A'} ; \widehat {B} = \widehat {B'} ; \widehat {C} = \widehat {C'}\)

Ta viết: ΔABC=ΔA′B′C′

Nếu 2 tam giác bằng nhau, ta suy ra tất cả các cạnh, các góc tương ứng bằng nhau.

2. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (c.c.c)

Nếu 3 cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

Ví dụ:

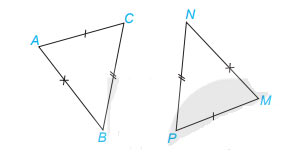
Xét ΔABC và ΔMNP

AB = MN

BC = NP

AC = MP

Vậy ΔABCΔ = ΔMNP (c.c.c)