Cách chứng minh 3 điểm thẳng hàng Chứng minh 3 điểm thẳng hàng lớp 7

Chứng minh 3 điểm thẳng hàng lớp 7 là một trong những dạng toán tương đối khó mà nhiều bạn học sinh chưa biết cách giải. Chính vì thế hôm nay Download.vn sẽ giới thiệu đến các bạn hướng dẫn chứng minh 3 điểm thẳng hàng lớp 7 chi tiết nhất.

Chứng minh 3 điểm thẳng hàng bao gồm toàn bộ kiến thức lý thuyết về khái niệm, các phương pháp chứng minh, ví dụ minh họa kèm theo một số bài tập có đáp án kèm theo tự luyện. Chứng minh 3 điểm thẳng hàng được biên soạn rất chi tiết dễ hiểu, gần gũi với các bạn học sinh. Qua đó các em dễ dàng nắm được kiến thức trọng tâm vận dụng vào giải các bài tập về chứng minh các điểm cùng nằm trên một đoạn thẳng. Bên cạnh đó các em tham khảo thêm: bài tập về lũy thừa số hữu tỉ, bài tập Nhân chia số hữu tỉ.

I. 3 điểm thẳng hàng là gì?

Khi ba điểm bất kỳ nào đó cùng thuộc một đường thẳng, thì ta nói ba điểm đó thẳng hàng.

Khi ba điểm bất kỳ nào đó không cùng thuộc bất kỳ đường thẳng nào, thì ta nói ba điểm đó không thẳng hàng.

Ví dụ 1. Hình 1 và Hình 2 dưới đây minh họa cho hai trường hợp: ba điểm thẳng hàng và ba điểm không thẳng hàng tương ứng.

Ở Hình 1: Ba điểm M, N và P cùng thuộc một đường thẳng, do đó ba điểm M, N và P thẳng hàng.

Ở Hình 2: Ba điểm D, E và F không cùng thuộc một đường thẳng, do đó ba điểm D, E và F không thẳng hàng

II. Vị trí tương đối của 3 điểm thẳng hàng

Trong 3 điểm thẳng hàng, ta có một và chỉ một điểm nằm giữa hai điểm còn lại.

Ví dụ 2. Quan sát ba điểm thẳng hàng M, N và P ở Hình 1, ta thấy:

+ Điểm M và điểm N nằm cùng phía đối với điểm P;

+ Điểm N và điểm P nằm cùng phía đối với điểm M;

+ Điểm M và điểm P nằm khác phía đối với điểm N;

+ Điểm N nằm ở giữa điểm M và điểm P.

III. Quan hệ của 3 điểm thẳng hàng

3 điểm thẳng hàng thì 3 điểm đó phân biệt và cùng nằm trên một đường thẳng.

Chỉ có một và chỉ một điểm nằm giữa hai điểm còn lại trong ba điểm thẳng hàng.

IV. Các phương pháp chứng minh 3 điểm thẳng hàng

• Sử dụng hai góc kề bù có ba điểm cần chứng minh thuộc hai cạnh là hai tia đối nhau.
• Ba điểm cần chứng minh thuộc cùng 1 tia hoặc một đường thẳng bất kì
• Hai đoạn thẳng đi qua 2 trong 3 điểm cần chứng minh cùng song song với một đường thẳng thứ 3
• Hai đường thẳng cùng đi qua hai trong ba điểm cần chứng minh cùng vuông góc với một đường thẳng thứ 3 nào đó.
• Đường thẳng đi qua 2 điểm cũng đi qua điểm thứ 3
• Áp dụng tính chất của đường phân giác của một góc, tính chất đường trung trực của đoạn thẳng hay tính chất ba đường cao trong tam giác
• Áp dụng các tính chất của hình bình hành
• Áp dụng tính chất của góc nội tiếp đường tròn
• Áp dụng tính chất của góc bằng nhau đối đỉnh
• Chứng minh bằng phương pháp phản chứng
• Chứng minh diện tích tam giác của 3 điểm bằng 0
• Áp dụng tính chất sự đồng quy của các đoạn thẳng

V. Cách chứng minh 3 điểm thẳng hàng

1. Phương pháp 1: (Hình 1)

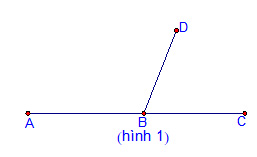
*Nếu \(\widehat{A B D}+\widehat{D B C}=180^{\circ}\) thì ba điểm A; B; C thẳng hàng.

Cơ sở lý thuyết: Góc có số đo bằng 180⁰ là góc bẹt

2. Phương pháp 2: ( Hình 2)

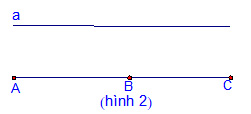
Nếu AB // a và AC // a thì ba điểm A; B; C thẳng hàng.

Cơ sở lý thuyết là: tiên đề Ơ – Clit- tiết 8- hình 7

3. Phương pháp 3: (Hình 3)

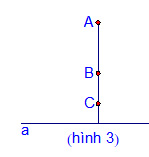
* Nếu AB \(\perp\) a ; AC \(\perp\)A thì ba điểm A; B; C thẳng hàng.

Cơ sở của phương pháp này là: Có một và chỉ một đường thẳng a’ đi qua điểm O và vuông góc với đường thẳng a cho trước

* Hoặc chứng minh A; B; C cùng thuộc một đường trung trực của một đoạn thẳng.

4. Phương pháp 4: ( Hình 4)

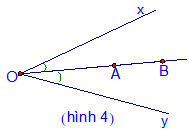
* Nếu tia OA và tia OB cùng là tia phân giác của góc xOy thì ba điểm O; A; B thẳng hàng.

Cơ sở của phương pháp này là: Mỗi góc có một và chỉ một tia phân giác .

* Hoặc : Hai tia OA và OB cùng nằm trên nửa mặt phẳng bờ chứa tia \(\widehat{xOA}= \widehat{xOB}\)  ba điểm O, A, B thẳng hàng.

5. Phương pháp 5: Nếu K là trung điểm BD, K’ là giao điểm của BD và AC. Nếu K’ là trung điểm BD thì K’≡ K thì A, K, C thẳng hàng.

Cơ sở của phương pháp này là: Mỗi đoạn thẳng chỉ có một trung điểm

VI. Ví dụ chứng minh 3 điểm thẳng hàng

Ví dụ 1: Cho tam giác ABC. Gọi D, E lần lượt là trung điểm của AB, AC. Trên tia đối của tia DC, lấy điểm M sao cho MD = CD. Trên tia đối của tia EB, lấy điểm N sao cho EN = BE. chứng minh : A là trung điểm của MN.

Gợi ý đáp án

Xét ΔBCD và ΔBMD, ta có :

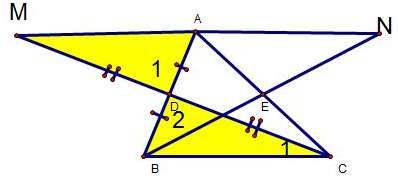
DB = DA (D là trung điểm của AB) ∠D1 = ∠D2 (đối đỉnh).

DC = DM (gt).

=> ΔBCD = ΔBMD (c -g -c)

=> ∠C1 = ∠M và BC = AM.

Mà : ∠C1; ∠M ở vị trí so le trong. => BC // AM.

Chứng minh tương tự, ta được : BC // AN và BC = AN.

Ta có : BC // AM (cmt) và BC // AN (cmt)

=> A, M. N thẳng hàng. (1)

BC = AM và BC = AN => AM = AN (2).

Từ (1) và (2), suy ra : A là trung điểm của MN.

Nhận xét: Chứng minh 3 điểm A, M, N thẳng hàng trước, sau đó chứng minh AM = AN

Ví dụ 2: Cho tam giác ABC vuông tại A. Trên nửa mặt phẳng bờ BC không chứa điểm A. Vẽ các điểm D và E sao cho BD vuông góc và bằng BA, vuông góc và bằng BC. Gọi M là trung điểm của CE. Chứng minh ba điểm A, D, M thẳng hàng.

Gợi ý đáp án

Kẻ MK ⊥ AB, MH ⊥ AC

Ta có M là trung điểm của CE

=> \(\Delta BME = \Delta BMC\left( {c - c - c} \right) \Rightarrow \widehat {EBM} = \widehat {CBM} = {45^0}\)

Mặt khác \(\widehat {EBC} = {90^0} \Rightarrow \widehat {KBE} + \widehat {ABC} = {90^0}\)

Mà \(\widehat {ACB} + \widehat {ABC} = {90^0} \Rightarrow \widehat {ACB} = \widehat {KBE} \Rightarrow \widehat {HCM} = \widehat {KBM}\)

Ta lại có BM = MC => \(\Delta BMK = \Delta HMC\) => MK = MH

=> \(\Delta AMK = \Delta HMA\) (cạnh huyền – cạnh góc vuông)

=> \(\widehat {KAM} = \widehat {HAM} = {45^0}\)

=> AM là tia phân giác của góc A

Mặt khác tam giác BAD vuông cân tại A

=> \(\widehat {BAD} = {45^0}\)

=> AD là tia phân giác của góc A

=> A, D, M thẳng hàng (vì cùng thuộc tia phân giác góc A)

VII. Bài tập chứng minh 3 điểm thẳng hàng lớp 7

1. PHƯƠNG PHÁP 1

Ví dụ 1. Cho tam giác ABC vuông ở A, M là trung điểm AC. Kẻ tia Cx vuông góc CA (tia Cx và điểm B ở hai nửa mặt phẳng đối nhau bờ AC). Trên tia Cx lấy điểm D sao cho CD = AB. Chứng minh ba điểm B, M, D thẳng hàng.

Ví dụ 2. Cho tam giác ABC. Trên tia đối của AB lấy điểm D mà AD = AB, trên tia đối tia AC lấy điểm E mà AE = AC. Gọi M; N lần lượt là các điểm trên BC và ED sao cho CM = EN. Chứng minh ba điểm M; A; N thẳng hàng.

Bài 1: Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AC, trên tia đối của tia AC lấy điểm E sao cho AE = AB. Gọi M, N lần lượt là trung điểm của BE và CD. Chứng minh ba điểm M, A, N thẳng hàng.

Bài 2: Cho tam giác ABC vuông ở A có \(\widehat{ABC}=60^{\circ}\). Vẽ tia Cx BC (tia Cx và điểm A ở phía ở cùng phía bờ BC), trên tia Cx lấy điểm E sao cho CE = CA. Trên tia đối của tia BC lấy điểm F sao cho BF = BA. Chứng minh ba điểm E, A, F thẳng hàng.

Bài 3: Cho tam giác ABC cân tại A, điểm D thuộc cạnh AB. Trên tia đối của tia CA lấy điểm E sao cho CE = BD. Kẻ DH và EK vuông góc với BC (H và K thuộc đường thẳng BC). Gọi M là trung điểm HK. Chứng minh ba điểm D, M, E thẳng hàng.

Bài 4: Gọi O là trung điểm của đoạn thẳng AB. Trên hai nửa mặt phẳng đối nhau bờ AB, kẻ Hai tia Ax và By sao cho \(\widehat{BAx}=\widehat{ABy}\) .Trên Ax lấy hai điểm C và E(E nằm giữa A và C), trên By lấy hai điểm D và F ( F nằm giữa B và D) sao cho AC = BD, AE = BF. Chứng minh ba điểm C, O, D thẳng hàng , ba điểm E, O, F thẳng hàng.

Bài 5. Cho tam giác ABC . Qua A vẽ đường thẳng xy // BC. Từ điểm M trên cạnh BC, vẽ các đường thẳng song song AB và AC, các đường thẳng này cắt xy theo thứ tự tại D và E. Chứng minh các đường thẳng AM, BD, CE cùng đi qua một điểm.

Bài 6: Cho tam giác ABC có AB < AC kẻ tia phân giác AD của góc BAC. Trên cạnh AC lấy điểm E sao cho AE = AB. Trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:

a) \(\Delta ADF = \Delta EDC\)

b) Chứng minh ba điểm E, F, D thẳng hàng

c) Chứng minh AD vuông góc với CF

Bài 7: Cho tam giác ABC vuông cân tại A. Vẽ ra phía ngoài tam giác ABC tam giác BCM cân tại M có góc ở đáy bằng 15⁰. Trên nửa mặt phẳng AB chứa điểm C, vẽ tam giác đều ABN. Chứng minh ba điểm M, N, B thẳng hàng.

Bài 8: Cho tam giác ABC vuông tại A. Trên nửa mặt phẳng bờ BC không chứa điểm A. Vẽ các điểm D và E sao cho BD vuông góc và bằng BA, vuông góc và bằng BC. Gọi M là trung điểm của CE. Chứng minh ba điểm A, D, M thẳng hàng.

2/ PHƯƠNG PHÁP 2

Ví dụ 1: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AC, AB. Trên Các đường thẳng BM và CN lần lượt lấy các điểm D và E sao cho M là trung điểm BD và N là trung điểm EC. Chứng minh ba điểm E, A, D thẳng hàng.

Ví dụ 2: Cho hai đoạn thẳng AC và BD cắt nhau tai trung điểm O của mỗi đoạn. Trên tia AB lấy lấy điểm M sao cho B là trung điểm AM, trên tia AD lấy điểm N sao cho D là trung điểm AN. Chúng minh ba điểm M, C, N thẳng hàng.

Bài 1. Cho tam giác ABC. Vẽ cung tròn tâm C bán kính AB và cung tròn tâm B bán kính AC. Đường tròn tâm A bán kính BC cắt các cung tròn tâm C và tâm B lần lượt tại E và F. ( E và F nằm trên cùng nửa mặt phẳng bờ BC chứa A). Chứng minh ba điểm F, A, E thẳng hàng.

III/ PHƯƠNG PHÁP 3

Ví dụ: Cho tam giác ABC có AB = AC. Gọi M là trung điểm BC.

a) Chứng minh AM BC.

b) Vẽ hai đường tròn tâm B và tâm C có cùng bán kính sao cho chúng cắt nhau tại hai điểm P và Q . Chứng minh ba điểm A, P, Q thẳng hàng.

Gợi ý: Xử dụng phương pháp 3 hoặc 4 đều giải được.

- Chứng minh AM , PM, QM cùng vuông góc BC

- hoặc AP, AQ là tia phân giác của góc BAC.

IV/ PHƯƠNG PHÁP 4

Ví dụ: Cho góc xOy .Trên hai cạnh Ox và Oy lấy lần lượt hai điểm B và C sao cho OB = OC. Vẽ đường tròn tâm B và tâm C có cùng bán kính sao cho chúng cắt nhau tại hai điểm A và D nằm trong góc xOy. Chứng minh ba điểm O, A, D thẳng hàng.

Gợi ý: Chứng minh OD và OA là tia phân giác của góc xOy

Bài 1. Cho tam giác ABC có AB = AC. Kẻ BM vuông góc AC, CN vuông góc AB, H là giao điểm của BM và CN.

a) Chứng minh AM = AN.

b) Gọi K là trung điểm BC. Chứng minh ba điểm A, H, K thẳng hàng.

Bài 2. Cho tam giác ABC có AB = AC. Gọi H là trung điểm BC. Trên nửa mặt phẳng bờ AB chứa C kẻ tia Bx vuông góc AB, trên nửa mặt phẳng bờ AC chứa B kẻ tia Cy vuông AC. Bx và Cy cắt nhau tại E. Chứng minh ba điểm A, H, E thẳng hàng.

V/ PHƯƠNG PHÁP 5

Ví dụ 1 . Cho tam giác ABC cân ở A. Trên cạnh AB lấy điểm M, trên tia đối tia CA lấy điểm N sao cho BM = CN. Gọi K là trung điểm MN. Chứng minh ba điểm B, K, C thẳng hàng

Gợi ý: Xử dụng phương pháp 5

Ví dụ 2. Cho tam giác \(\mathrm{ABC}\) cân ở \(\mathrm{A}, \widehat{B A C}=108^{\circ}\), Gọi \(\mathrm{O}\) là một điểm nằm trên tia phân giác của góc C sao cho \(\widehat{C B O}=12^{\circ}\). Vẽ tam giác đều \(\mathrm{BOM}\) (M và A cùng thuộc một nửa mặt phẳng bờ BO). Chứng minh ba điểm C, A, M thẳng hàng.

Gợi ý: Chứng minh \(\widehat{O C A}=\widehat{O C M}\) từ đó suy ra tia \(\mathrm{CA}\) và tia CM trùng nhau.

................

Mời các bạn tải File tài liệu để xem thêm nội dung chi tiết