Toán 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác Giải Toán lớp 7 trang 63 - Tập 1 sách Kết nối tri thức với cuộc sống

Giải Toán lớp 7 bài 13: Hai tam giác bằng nhau, Trường hợp bằng nhau thứ nhất của tam giác bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 7 Tập 1 Kết nối tri thức với cuộc sống trang 63, 64, 65, 66, 67.

Lời giải Toán 7 Bài 13 Kết nối tri thức trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 7, từ đó học tốt môn Toán lớp 7 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài 13 Chương IV - Tam giác bằng nhau. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 7 Kết nối tri thức với cuộc sống tập 1 bài 13 - Luyện tập

Luyện tập 1

Cho tam giác ABC bằng tam giác DEF (H.4.13). Biết rằng BC = 4cm, . Hãy tính độ dài đoạn thẳng EF và số đo góc EDF.

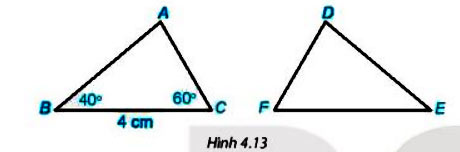
Gợi ý đáp án:

Xét tam giác ABC có

Tổng ba góc của tam giác bằng 180⁰

=> \(\widehat A + \widehat B + \widehat C = {180^0}\)

=> \(\widehat A = {180^0} - \left( {\widehat B + \widehat C} \right) = {180^0} - \left( {{{40}^0} + {{60}^0}} \right) = {80^0}\)

Ta có ∆ABC = ∆DEF

=> BC = EF = 4cm (Hai cạnh tương ứng bằng nhau)

Ta có ∆ABC = ∆DEF

=> \(\widehat A = \widehat {FDE} = {80^0}\) (Hai góc tương ứng bằng nhau)

Vậy độ dài đoạn thẳng EF là 4cm, số đo góc \(\widehat {FDE}\) là 80⁰.

Luyện tập 2

Cho hình 4.17, biết AB =AD, BC = DC. Chứng minh rằng ∆ABC = ∆ADC

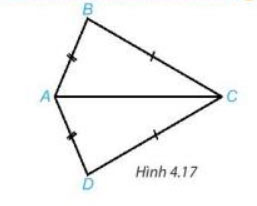
Gợi ý đáp án:

Xét hai tam giác ABC và ADC có:

Cạnh AC là cạnh chung

AB =AD (giả thiết)

BC = DC (giả thiết)

=> ∆OBM = ∆OAM (c – c – c)

Giải Toán 7 Kết nối tri thức với cuộc sống trang 67 tập 1

Bài 4.4

Cho tam giác ABC và DEF như hình 4.18. Trong các khẳng định sau, khẳng định nào đúng?

(1) \(\Delta ABC = \Delta DEF\)

(2) \(\Delta ACB = \Delta EDF\)

(3) \(\Delta BAC = \Delta DFE\)

(4) \(\Delta CAB = \Delta DEF\)

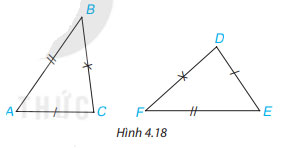
Gợi ý đáp án:

Xét tam giác \(\Delta ACB\) và \(\Delta EDF\) có:

\(\begin{array}{l}AC = ED\\AB = EF\\CB = DF\end{array}\)

\(\Rightarrow \Delta ACB = \Delta EDF(c.c.c)\)

Xét tam giác \(\Delta CAB\) và \(\Delta DEF\) có:

\(\begin{array}{l}CA = DE\\AB = EF\\CB = DF\end{array}\)

\(\Rightarrow \Delta CAB = \Delta DEF(c.c.c)\)

Vậy khẳng định (2) và (4) đúng.

Chú ý: Khi \(\Delta ABC = \Delta DEF\), ta cũng có thể viết \(\Delta BAC = \Delta EDF\) hay \(\Delta CBA = \Delta FED\);....

Bài 4.5

Trong Hình 4.19, hãy chỉ ra hai cặp tam giác bằng nhau.

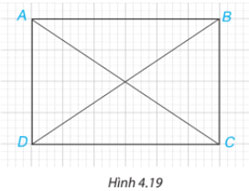
Gợi ý đáp án:

+) Xét \(\Delta ABC\) và \(\Delta CDA\) có:

AB=CD

DB chung

BC=AD

\(\Rightarrow \Delta ABC=\Delta CDA(c.c.c)\)

+) Xét \(\Delta ABD\) và \(\Delta CDB\) có:

AB=CD

DB chung

AD=CB

\(\Rightarrow \Delta ABD=\Delta CDB(c.c.c)\)

Bài 4.6

Cho Hình 4.20, biết \(AB = CB, AD = CD,\widehat{DAB} = {90^\circ },\widehat{BDC} = {30^\circ }\)

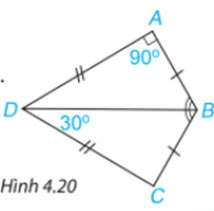
a) Chứng minh rằng \(\Delta ABD = \Delta CBD\).

b) Tính \(\widehat {ABC}\).

Gợi ý đáp án:

a) Xét \(\Delta ABD\) và \(\Delta CBD\) có:

DA=DC(gt)

BD chung

BA=BC

Vậy \(\Delta ABD = \Delta CBD(c.c.c)\)

b) Ta có \(\widehat A = \widehat C = {90^o}\)(hai góc tương ứng)

\(\begin{array}{l}\widehat C + \widehat {CDB} + \widehat {DBC} = {180^o}\\ \Rightarrow {90^o} + {30^o} + \widehat {DBC} = {180^o}\\ \Rightarrow \widehat {DBC} = {60^o}\end{array}\)

Mà \(\Delta ABD = \Delta CBD\) nên \(\widehat {ABD} = \widehat {CBD}\) (2 góc tương ứng)

\(\Rightarrow \widehat {ABD} = \widehat {CBD} = {60^o}\\\Rightarrow \widehat {ABC} = \widehat {ABD} + \widehat {CBD} = {60^o} + {60^o} = {120^o}\)