Toán 7 Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc Giải Toán lớp 7 trang 40 - Tập 1 sách Kết nối tri thức với cuộc sống

Bài trước

Mục lục

Bài sau

Giải bài tập Toán lớp 7 Bài 8: Góc ở vị trí đặc biệt, Tia phân giác của một góc với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 7 Tập 1 Kết nối tri thức với cuộc sống trang 40, 41, 42, 43, 44, 45. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 7 Bài 8 chi tiết phần câu hỏi, luyện tập, bài tập, đồng thời còn giúp các em hệ thống lại toàn bộ kiến thức lý thuyết trọng tâm của Bài 8 Chương III: Góc và đường thẳng song song. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 7 bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc sách Kết nối tri thức với cuộc sống

Phần Luyện tập
Phần Vận dụng
Phần Bài tập

Phần Luyện tập

Luyện tập 1 trang 42 Toán 7 tập 1

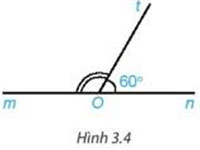
Viết tên hai góc kề bù trong Hình 3.4 và tính số đo góc mOt.

Hình 3.4

Lời giải:

Hai góc kề bù trong Hình 3.4 là góc mOt và góc nOt.

Do góc mOt và góc nOt là hai góc kề bù nên tổng số đo hai góc mOt và góc nOt bằng 180^o.

Khi đó số đo góc mOt bằng 180^o – 60^o = 120^o.

Vậy số đo góc mOt bằng 120^o.

Luyện tập 2 trang 43 Toán 7 tập 1

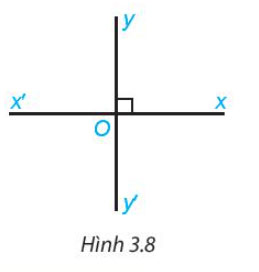
Hai đường thẳng xx' và yy' cắt nhau tại O sao cho góc xOy vuông (H.3.8). Khi đó các góc yOx', x'Oy', xOy' cũng đều là góc vuông. Vì sao?

Lời giải:

Góc xOy và xOy' là hai góc kề bù nên tổng số đo góc xOy và xOy' bằng 180^o.

Mà góc xOy bằng 90^o nên góc xOy' bằng 180^o– 90^o= 90^o.

Góc xOy và góc x'Oy' là hai góc đối đỉnh nên góc x'Oy' bằng 90^o.

Góc x'Oy và góc xOy' là hai góc đối đỉnh nên góc x'Oy bằng 90^o.

Do đó các góc đều là góc vuông.

Luyện tập 3 trang 45 Toán 7 tập 1

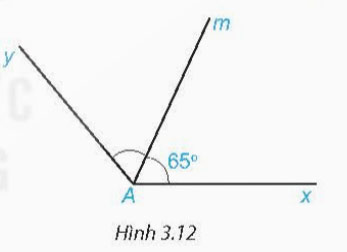
Cho góc xAm có số đo bằng 65⁰ và Am là tia phân giác của góc xAy (H.3.12). Tính số đo góc xAy.

Hình 3.12

Lời giải:

Ta có:

Am là tia phân giác của góc xAy thì $\widehat {xAm} = \widehat {yAm} = \frac{1}{2}\widehat {xAy}$ $\widehat {xAm} = \widehat {yAm} = \frac{1}{2}\widehat {xAy}$

$\Rightarrow \frac{1}{2}\widehat {xAy} = {65^0} \Rightarrow \widehat {xAy} = {65^0}.2 = {130^0}$ $\Rightarrow \frac{1}{2}\widehat {xAy} = {65^0} \Rightarrow \widehat {xAy} = {65^0}.2 = {130^0}$

Vậy số đo góc xAy là 130⁰

Phần Vận dụng

Quan sát hình vẽ bên.

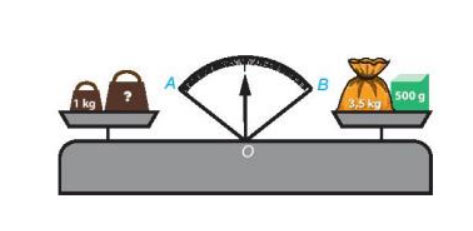
Vận dụng

Quả cân ở đĩa cân bên trái nặng bao nhiêu kilogam để cân thăng bằng, tức là kim trên mặt đồng hồ của cân là tia phân giác của góc AOB?

Gợi ý đáp án:

Để cân thăng bằng (tức là kim trên mặt đồng hồ của cân là tia phân giác của góc AOB) thì số kilogam bên trái bằng số kilogam bên phải.

Đổi 500g = 0,5kg

Ta có: Khối lượng cân bên phải là:

3,5 + 0,5 = 4 (kg)

Khối lượng quả cân ở đĩa cân bên trái cần tìm là:

4 – 1 = 3 (kg)

Vậy quả cân ở đĩa cân bên trái nặng 3kg thì cân thăng bằng.

Phần Bài tập

Bài 3.1 trang 45 Toán 7 tập 1

Cho hình 3.13, hãy kể tên các cặp góc kề bù.

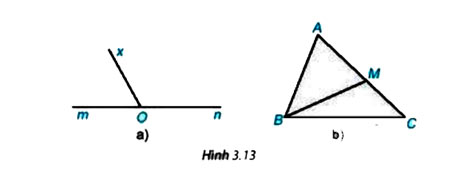
Hình 3.13

Gợi ý đáp án:

Các cặp góc kề bù hình 3.13a: $\widehat {mOx},\widehat {xOn}$ $\widehat {mOx},\widehat {xOn}$

Các cặp góc kề bù hình 3.13b: $\widehat {AMB},\widehat {BMC}$ $\widehat {AMB},\widehat {BMC}$

Bài 3.2 trang 45 Toán 7 tập 1

Cho hình 3.14, hãy kể tên các cặp góc đối đỉnh.

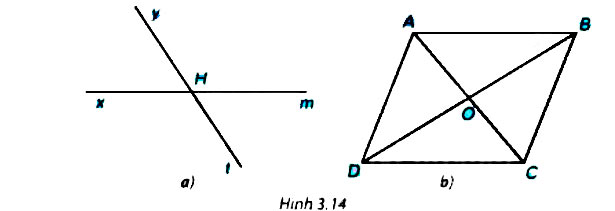
Hình 3.14

Gợi ý đáp án:

- Các cặp góc đối đỉnh hình 3.14a:

$\widehat {yHx},\widehat {mHt}$ $\widehat {yHx},\widehat {mHt}$

$\widehat {yHm},\widehat {xHt}$ $\widehat {yHm},\widehat {xHt}$

- Các cặp góc đối đỉnh hình 3.14b:

$\widehat {AOB},\widehat {DOC}$ $\widehat {AOB},\widehat {DOC}$

$\widehat {AOD},\widehat {BOC}$ $\widehat {AOD},\widehat {BOC}$

Bài 3.3 trang 45 Toán 7 tập 1

Vẽ góc xOy có số đo bằng 60⁰. Vẽ tia Om là tia đối của tia Ox.

a) Gọi tên hai góc kề bù có trong hình vừa vẽ.

b) Tính số đo góc yOm.

c) Vẽ tia Ot là tia phân giác của góc xOy. Tính số đo các góc tOy và tOm.

Gợi ý đáp án:

Hình vẽ minh họa:

a) Hai góc kề bù có trong hình vẽ là góc xOy và góc yOm.

b) Quan sát hình vẽ ta có:

Góc xOy và góc yOm là hai góc kề bù (câu a)

Suy ra: $\widehat {xOy} + \widehat {yOm} = {180^0}$ $\widehat {xOy} + \widehat {yOm} = {180^0}$

$\begin{matrix} {60^0} + \widehat {yOm} = {180^0} \hfill \\ \Rightarrow \widehat {yOm} = {180^0} - {60^0} = {130^0} \hfill \\ \end{matrix}$ $\begin{matrix} {60^0} + \widehat {yOm} = {180^0} \hfill \\ \Rightarrow \widehat {yOm} = {180^0} - {60^0} = {130^0} \hfill \\ \end{matrix}$

Vậy góc yOm có số đo là 130⁰

c) Theo bài ra ta có:

Ot là tia phân giác của góc xOy

=> $\widehat {xOt} = \widehat {yOt} = \frac{{\widehat {xOy}}}{2} = \frac{{{{60}^0}}}{2} = {30^0}$ $\widehat {xOt} = \widehat {yOt} = \frac{{\widehat {xOy}}}{2} = \frac{{{{60}^0}}}{2} = {30^0}$

Ta có:

$\widehat {tOm} = \widehat {yOm} + \widehat {yOt} = {130^0} + {30^0} = {160^0}$ $\widehat {tOm} = \widehat {yOm} + \widehat {yOt} = {130^0} + {30^0} = {160^0}$

(Hay $\widehat {tOm} = {180^0} - \widehat {xOt} = {180^0} - {30^0} = {160^0}$ $\widehat {tOm} = {180^0} - \widehat {xOt} = {180^0} - {30^0} = {160^0}$)

Bài 3.4 trang 45 Toán 7 tập 1

Cho hình 3.15a, biết $\widehat {DMA} = {45^0}$ $\widehat {DMA} = {45^0}$ . Tính số đo góc DMB.

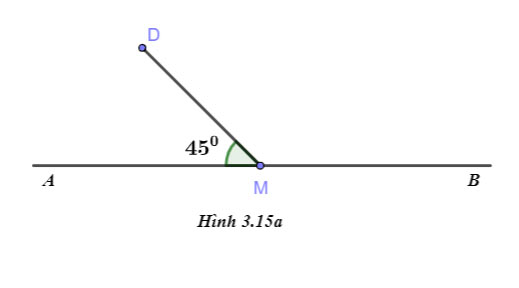
Hình 3.15a

Gợi ý đáp án:

Quan sát hình vẽ ta có:

Góc DMA và góc DMB là hai góc kề bù

Suy ra: $\widehat {DMA} + \widehat {DMB} = {180^0}$ $\widehat {DMA} + \widehat {DMB} = {180^0}$

$\begin{matrix} {45^0} + \widehat {DMB} = {180^0} \hfill \\ \Rightarrow \widehat {DMB} = {180^0} - {45^0} = {135^0} \hfill \\ \end{matrix}$ $\begin{matrix} {45^0} + \widehat {DMB} = {180^0} \hfill \\ \Rightarrow \widehat {DMB} = {180^0} - {45^0} = {135^0} \hfill \\ \end{matrix}$

Bài 3.5 trang 45 Toán 7 tập 1

Cho hình 3.15b, biết $\widehat {xBm} = {36^0}$ $\widehat {xBm} = {36^0}$ . Tính số đo các góc còn lại trong hình vẽ.

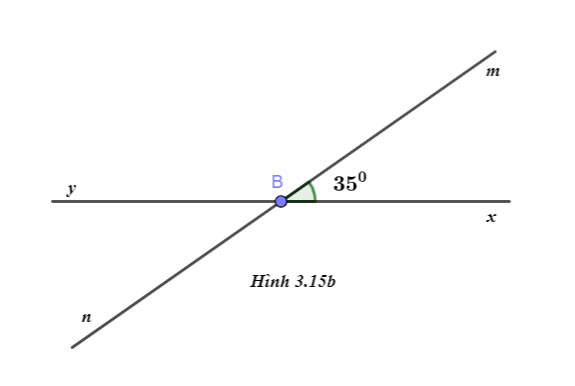
Hình 3.15b

Gợi ý đáp án:

Quan sát hình vẽ ta có:

Góc mBx và góc mBy là hai góc kề bù

Suy ra: $\widehat {xBm} + \widehat {mBy} = {180^0}$ $\widehat {xBm} + \widehat {mBy} = {180^0}$

$\begin{matrix} {36^0} + \widehat {mBy} = {180^0} \hfill \\ \Rightarrow \widehat {mBy} = {180^0} - {36^0} = {144^0} \hfill \\ \end{matrix}$ $\begin{matrix} {36^0} + \widehat {mBy} = {180^0} \hfill \\ \Rightarrow \widehat {mBy} = {180^0} - {36^0} = {144^0} \hfill \\ \end{matrix}$

Góc mBx và góc yBn là hai góc đối đỉnh

Suy ra: $\widehat {xBm} = \widehat {yBn} = {36^0}$ $\widehat {xBm} = \widehat {yBn} = {36^0}$

Góc mBy và góc nBx là hai góc đối đỉnh

Suy ra: $\widehat {yBm} = \widehat {nBx} = {144^0}$ $\widehat {yBm} = \widehat {nBx} = {144^0}$

Chia sẻ bởi: