Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn (không bao gồm tài liệu cao cấp) và trải nghiệm website không quảng cáo
Tìm hiểu thêm »Giải bài tập Toán lớp 7 Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác với lời giải chi tiết, rõ ràng theo khung chương trình SGK Toán 7 Tập 2 Kết nối tri thức với cuộc sống trang 59, 60, 61, 62. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.
Giải Toán 7 Bài 31 chi tiết phần câu hỏi, luyện tập, bài tập, đồng thời còn giúp các em hệ thống lại toàn bộ kiến thức lý thuyết trọng tâm của Bài 31 Chương IX: Quan hệ giữa các yếu tố trong một tam giác. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
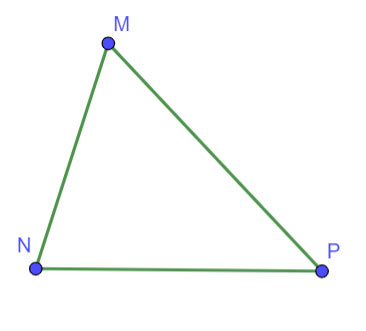
Cho tam giác MNP có độ dài các cạnh: MN = 3 cm, NP = 5 cm, MP = 7 cm. Hãy xác định góc đối diện với từng cạnh rồi sắp xếp các góc của tam giác MNP theo thứ tự từ bé đến lớn.
Gợi ý đáp án:
Góc đối diện với cạnh MN là ![]() \(\widehat P\)
\(\widehat P\)
Góc đối diện với cạnh NP là ![]() \(\widehat M\)
\(\widehat M\)
Góc đối diện với cạnh MP là ![]() \(\widehat N\)
\(\widehat N\)
Do MN < NP < MP nên ![]() \(\widehat P < \widehat M < \widehat N\)
\(\widehat P < \widehat M < \widehat N\)
Các góc của tam giác MNP theo thứ tự từ bé đến lớn là: ![]() \(\widehat P;\widehat M;\widehat N\)
\(\widehat P;\widehat M;\widehat N\)
Cho tam giác MNP có ![]() \(\widehat M = {47^0};\widehat N = {53^0}\) . Hãy viết các cạnh của tam giác đó theo thứ tự độ dài từ bé đến lớn.
\(\widehat M = {47^0};\widehat N = {53^0}\) . Hãy viết các cạnh của tam giác đó theo thứ tự độ dài từ bé đến lớn.
Gợi ý đáp án:
Hình vẽ minh họa:
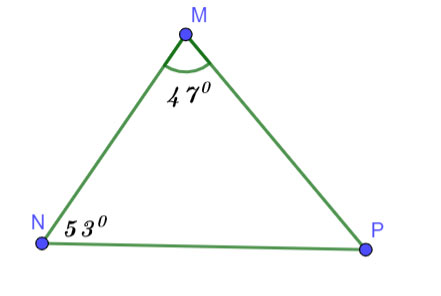
Xét tam giác MNP:
 \(\begin{matrix}
\widehat M + \widehat N + \widehat P = {180^0} \hfill \\
\Rightarrow \widehat P = {180^0} - \left( {\widehat M + \widehat N} \right) \hfill \\
\Rightarrow \widehat C = {180^0} - \left( {{{47}^0} + {{53}^0}} \right) = {80^0} \hfill \\
\end{matrix}\)
\(\begin{matrix}
\widehat M + \widehat N + \widehat P = {180^0} \hfill \\
\Rightarrow \widehat P = {180^0} - \left( {\widehat M + \widehat N} \right) \hfill \\
\Rightarrow \widehat C = {180^0} - \left( {{{47}^0} + {{53}^0}} \right) = {80^0} \hfill \\
\end{matrix}\)
Do 47o < 53o < 80o => ![]() \(\widehat M < \widehat N < \widehat P\)
\(\widehat M < \widehat N < \widehat P\)
Cạnh NP là đối diện với ![]() \(\widehat M\)
\(\widehat M\)
Cạnh MP là đối diện với ![]() \(\widehat N\)
\(\widehat N\)
Cạnh MN là đối diện với ![]() \(\widehat P\)
\(\widehat P\)
=> NP < MP < MN
Vậy các cạnh theo thứ tự từ bé đến lớn là: NP, MP, MN
Em hãy trả lời câu hỏi trong tình huống mở đầu.
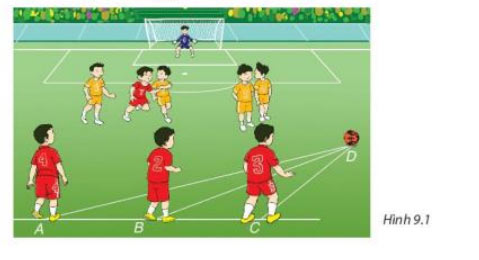
Trong trận bóng đá, trái bóng đang ở vị trí D, ba cầu thủ đứng thẳng hàng tại vị trí A, B, C trên sân với số áo lần lượt là 4, 2, 3 như Hình 9.1. Theo em, cầu thủ nào gần trái bóng nhất, cầu thủ nào xa trái bóng nhất? Tại sao? (Biết rằng góc ACD là góc tù).
Gợi ý đáp án:
Xét tam giác ABD có:
![]() \(\widehat {ABD}\) là góc tù =>
\(\widehat {ABD}\) là góc tù => ![]() \(\widehat {ABD}\) là góc lớn nhất trong tam giác ABD
\(\widehat {ABD}\) là góc lớn nhất trong tam giác ABD
=> AD > BD
Xét tam giác BCD có:
![]() \(\widehat {BCD}\) là góc tù =>
\(\widehat {BCD}\) là góc tù => ![]() \(\widehat {BCD}\) là góc lớn nhất trong tam giác BCD
\(\widehat {BCD}\) là góc lớn nhất trong tam giác BCD
=> BD > CD
=> AD > BD > CD
Vậy cầu thủ mang áo số 4 xa trái bóng nhất.
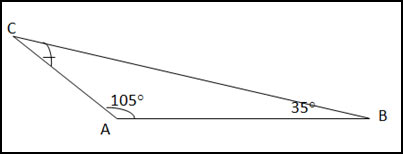
Cho tam giác ABC có ![]() \(\widehat{A} = 105°, \widehat{B} = 35°\)
\(\widehat{A} = 105°, \widehat{B} = 35°\)
a) Tam giác ABC là tam giác gì ?
b) Tìm cạnh lớn nhất của tam giác ABC
Gợi ý đáp án:
a) Ta có ![]() \(\widehat{A} = 105°\). Suy ra
\(\widehat{A} = 105°\). Suy ra ![]() \(90° < \widehat{A} < 180°, \widehat{A}\) là góc tù. Tam giác ABC là tam giác tù.
\(90° < \widehat{A} < 180°, \widehat{A}\) là góc tù. Tam giác ABC là tam giác tù.
b) Số đo góc ![]() \(\widehat{C}\) là:
\(\widehat{C}\) là: ![]() \(180°- (105° + 35°) = 180° - 140° = 40°\)
\(180°- (105° + 35°) = 180° - 140° = 40°\)
Vậy trong tam giác ABC ta có![]() \(\widehat{A} > \widehat{C} > \widehat{B}\)
\(\widehat{A} > \widehat{C} > \widehat{B}\)
Theo định lý ta có, BC > AB > AC
Vậy BC chính là cạnh lớn nhất của tam giác ABC.
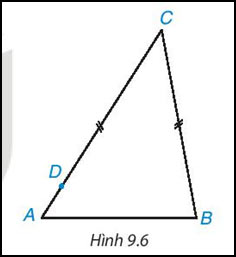
Trong hình 9.6 có hai đoạn thẳng BC và DC bằng nhau, D nằm giữa A và C. Hỏi, kết luận nào trong các kết luận sau là đúng ? Tại sao
a) ![]() \(\widehat{A}= \widehat{B}\)
\(\widehat{A}= \widehat{B}\)
b) ![]() \(\widehat{A}> \widehat{B}\)
\(\widehat{A}> \widehat{B}\)
c) ![]() \(\widehat{A}< \widehat{B}\)
\(\widehat{A}< \widehat{B}\)
Gợi ý đáp án:
Theo hình ta có AC = AD + DC
Mà DC= BC. Suy ra AC= AD+ BC. Ta có AC > BC hay BC < AC
Theo định lý, ta có ![]() \(\widehat{A}< \widehat{B}\)
\(\widehat{A}< \widehat{B}\)
Vậy kết luận c) là kết luận đúng
Trong tam giác cân có một góc bằng 96°, hỏi cạnh lớn nhất của tam giác cân đó là cạnh bên hay cạnh đáy? Vì sao?
Gợi ý đáp án:
Tam giác cân có 1 góc bằng 96°. Ta gọi góc đó là ![]() \(\widehat{A}. 90° < 96°<180°\).
\(\widehat{A}. 90° < 96°<180°\).
Vậy suy ra ![]() \(\widehat{A}\) là góc tù,
\(\widehat{A}\) là góc tù, ![]() \(\widehat{A}\) lớn nhất trong tam giác cân ABC
\(\widehat{A}\) lớn nhất trong tam giác cân ABC
Một tam giác chỉ có một góc tù, góc tù ![]() \(\widehat{A}\) lớn nhất . Suy ra
\(\widehat{A}\) lớn nhất . Suy ra ![]() \(\widehat{A}\) là góc ở đỉnh tam giác cân
\(\widehat{A}\) là góc ở đỉnh tam giác cân
Theo định lý, ta có cạnh lớn nhất của tam giác cân đó là cạnh đáy.
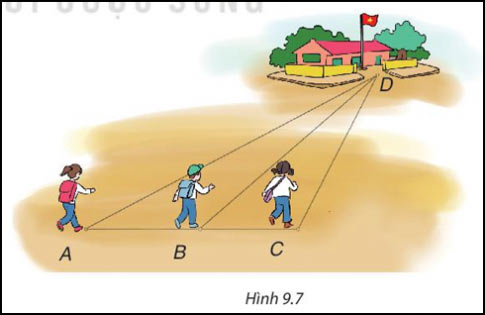
Ba bạn Mai, Việt, Hà đi đến trường tại địa điểm D lần lượt theo 3 con đường AD, BD, CD (H.9.7). Biết rằng ba điểm A,B,C cùng nằm trên một đường thẳng, B nằm giữa A và C, ![]() \(\widehat{ACD}\) là góc tù. Hỏi bạn nào đi xa nhất, bạn nào đi gần nhất? Vì sao?
\(\widehat{ACD}\) là góc tù. Hỏi bạn nào đi xa nhất, bạn nào đi gần nhất? Vì sao?
Gợi ý đáp án:
Ta có ![]() \(\widehat{ACD}\) là góc tù. Vậy
\(\widehat{ACD}\) là góc tù. Vậy ![]() \(\widehat{ACD}\) là góc lớn nhất trong tam giác ACD. Theo định lý, ta có AD là cạnh có độ dài lớn nhất tam giác ACD
\(\widehat{ACD}\) là góc lớn nhất trong tam giác ACD. Theo định lý, ta có AD là cạnh có độ dài lớn nhất tam giác ACD
Vậy Mai là người đi xa nhất.
B thuộc đường thẳng AC. Vậy ![]() \(\widehat{BCD}= \widehat{ACD}\). Suy ra
\(\widehat{BCD}= \widehat{ACD}\). Suy ra ![]() \(\widehat{BCD}\) là góc tù của tam giác BCD. Vậy theo định lý, cạnh BD lớn hơn cạnh CD
\(\widehat{BCD}\) là góc tù của tam giác BCD. Vậy theo định lý, cạnh BD lớn hơn cạnh CD
Vậy Việt sẽ đi xa hơn Hà. Hà là người đi ngắn nhất.
Ba địa điểm A,B,C là ba đỉnh của một tam giác ABC với ![]() \(\widehat{A}\) tù, AC= 500m. Đặt một loa truyền thanh tại một điểm nằm giữa A và B thì tại C có thể nghe thấy tiếng loa không nếu bán kính để nghe rõ tiếng của loa là 500m?
\(\widehat{A}\) tù, AC= 500m. Đặt một loa truyền thanh tại một điểm nằm giữa A và B thì tại C có thể nghe thấy tiếng loa không nếu bán kính để nghe rõ tiếng của loa là 500m?
Gợi ý đáp án:
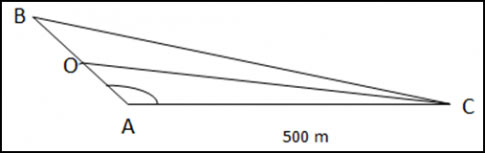
Gọi điểm đặt loa truyền thanh là O. O thuộc đoạn AB nằm giữa A và B nên O là trung điểm của AB. OC chính là khoảng cách từ điểm đặt loa cho đến điểm C.
Ta có ![]() \(\widehat{A}\) tù, suy ra
\(\widehat{A}\) tù, suy ra ![]() \(\widehat{OAC}\) là góc lớn nhất tam giác OAC. Theo định lý, ta có OC chính là cạnh có độ dài lớn nhất tam giác OAC.
\(\widehat{OAC}\) là góc lớn nhất tam giác OAC. Theo định lý, ta có OC chính là cạnh có độ dài lớn nhất tam giác OAC.
Từ trên, suy ra OC > AC. Mà AC = 500m = bán kính để nghe rõ tiếng của loa đặt ở điểm O. Ta có OC> bán kính để nghe rõ tiếng loa.
Kết luận: tại điểm C sẽ không thể nghe thấy tiếng loa.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: