Bài tập các trường hợp bằng nhau của hai tam giác Ôn tập Hình học lớp 7

Tải về Bình luận

Bài tập các trường hợp bằng nhau của hai tam giác là một trong những dạng toán tương đối khó mà nhiều bạn học sinh chưa biết cách giải. Chính vì thế hôm nay Download.vn sẽ giới thiệu đến các bạn các dạng bài tập về hai tam giác bằng nhau lớp 7 chi tiết nhất.

Các dạng bài tập về hai tam giác bằng nhau lớp 7

Các dạng bài tập về hai tam giác bằng nhau bao gồm toàn bộ kiến thức lý thuyết về các trường hợp bằng nhau của tam giác, một số bài tập tự luận, trắc nghiệm có đáp án giải chi tiết và 16 bài tập tự luyện. Các dạng bài tập về hai tam giác bằng nhau được biên soạn rất chi tiết dễ hiểu, gần gũi với các bạn học sinh. Qua đó các em dễ dàng nắm được kiến thức trọng tâm vận dụng vào giải các bài tập. Bên cạnh đó các em tham khảo thêm: bài tập về lũy thừa số hữu tỉ, bài tập Nhân chia số hữu tỉ.

Bài tập các trường hợp bằng nhau của hai tam giác

1. Các trường hợp bằng nhau của tam giác
2. Ứng dụng các trường hợp bằng nhau của tam giác
3. Bài tập các trường hợp bằng nhau (Có đáp án)

1. Các trường hợp bằng nhau của tam giác

a) Trường hợp 1: cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

b) Trường hợp 2: cạnh – góc – cạnh: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

c) Trường hợp 3: góc – cạnh – góc: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

2. Ứng dụng các trường hợp bằng nhau của tam giác

Chúng ta thường vận dụng các trường hợp bằng nhau của tam giác để:

Chứng minh: hai tam giác bằng nhau, hai đoạn thẳng bằng nhau, hai góc bằng nhau; hai đường thẳng vuông góc; hai đường thẳng song song; ba điểm thẳng hàng; …
Tính: các độ dài đoạn thẳng; tính số đo góc; tính chu vi; diện tích; …
So sánh: các độ dài đoạn thẳng; so sánh các góc; …

3. Bài tập các trường hợp bằng nhau (Có đáp án)

I. Bài tập trắc nghiệm

Câu 1: Cho ∆ PQR = ∆ DEF trong đó PQ = 4cm, QR = 6cm, PR = 5cm. Chu vi tam giác DEF là:

A. 14cm	B. 15cm
C. 16cm	D. 17cm

Câu 2: Cho ΔABC = ΔMNP. Biết AB = 5cm, MP = 7cm và chu vi của tam giác ABC bằng 22cm. Tính các cạnh còn lại của mỗi tam giác?

A. NP = BC = 9cm	B. NP = BC = 11cm
C. NP = BC = 10cm	D. NP = 9cm; BC = 10cm

Câu 3: Cho DΔABC = ΔMNP có AB = 7cm, AC = 10cm, NP = 12cm. Tính chu vi tam giác MNP:

A. 27cm	B. 29cm
C. 32cm	D. 37cm

Câu 4: Cho ΔIEF = ΔMNO. Hãy tìm cạnh tương ứng với cạnh EF, góc tương ứng với góc E:

A.MN và góc O

B.MO và góc M

C.NO và góc N

Câu 5: Cho hai tam giác bằng nhau: Tam giác ABC (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) và môt tam giác có ba đỉnh là T, S, R. Hãy viết kí hiệu về sự bằng nhau của hai tam giác đó biết rằng góc A bằng góc T và AC = TS.

A. ΔABC = ΔTRS	B. ΔABC = ΔRTS
C. ΔABC = ΔSTR	D. ΔABC = ΔTSR

Câu 6: Cho △ABC=△DEF. Biết rằng AB = 5cm; AC = 12cm; EF = 12cm. Tính chu vi tam giác DEF là

A. 30cm

B. 22 cm

C. 18 cm

D. 20 cm

Câu 7: Cho △ABC=△DEF. Biết rằng AB = 6cm; AC = 8cm; EF = 10cm. Tính chu vi tam giác DEF là

A. 24cm

B. 20cm

C. 18 cm

D. 30 cm

Câu 8: Cho △DEF=△MNP. Biết EF+FD=10cm; NP−MP=2cm; DE=3cm. Tính độ dài cạnh FD

A. 4 cm

B. 6 cm

C. 8 cm

D. 10 cm

ĐÁP ÁN

Câu 1	Câu 2	Câu 3	Câu 4	Câu 5
B	C	B	C	A
Câu 6	Câu 7	Câu 8
A	A	A

II. Bài tập tự luận

a) Trường hợp 1: cạnh – cạnh – cạnh

Bài 1: Cho tam giác ABC. Vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm C bán bính BA, chúng cách nhau giữa ở D (D và B nằm khác phía đối với bờ AC). Chứng minh rằng AD // BC

Gợi ý đáp án

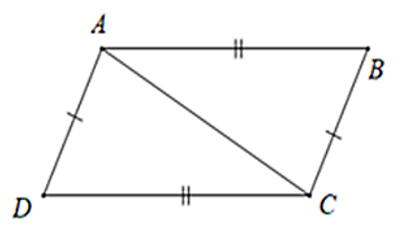
Xét ΔABC và ΔCDA có AC chung

AB = CD (gt)

BC = DA (gt)

Nên ΔABC = ΔCDA (c-c-c)

⇒ $\widehat{ABC}=\widehat{CAD}$ $\widehat{ABC}=\widehat{CAD}$ (hai góc tương ứng bằng nhau)

mà hai góc ở vị trí so le trong

Do đó AD // BC

Bài 2: Tam giác ABC có AB = AC, M là trung điểm của BC. Chứng mình rằng AM vuông góc với BC.

Gợi ý đáp án

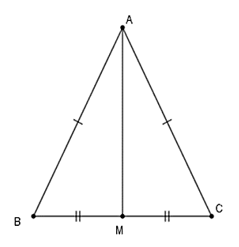
Xét ΔAMB và ΔAMC có:

AB = AC

AM chung

MB = MC (gt)

⇒ ΔAMB = ΔAMC (c-c-c)

Suy ra $\widehat{BAM}=\widehat{CAM};\widehat{AMB}=\widehat{AMC}$ $\widehat{BAM}=\widehat{CAM};\widehat{AMB}=\widehat{AMC}$(góc tương ứng bằng nhau)

Mà $\widehat{AMB}+\widehat{AMC}={180}^0$ $\widehat{AMB}+\widehat{AMC}={180}^0$(hai góc kề bù)

Nên $\widehat{AMB}=\widehat{AMC}=\frac{{180}^0}{2}={90}^0$ $\widehat{AMB}=\widehat{AMC}=\frac{{180}^0}{2}={90}^0$ hay AM ⊥ BC

b) Trường hợp 2: cạnh – góc – cạnh

Bài 1: Cho đoạn thẳng BC. Gọi A là một điểm nằm trên đường trung trực xy của đoạn thẳng BC và M là giao điểm của xy với BC. Chứng minh AB = AC

Lời giải

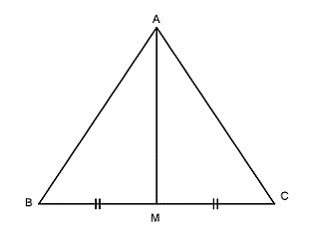
Xét hai tam giác AMB và AMC có:

MB = MC (gt)

$\widehat{AMB}=\widehat{AMC}={90}^0$ $\widehat{AMB}=\widehat{AMC}={90}^0$ (vì AM ⊥ BC)

AH là cạnh chung

Nên ΔAMB = ΔAMC (c-g-c)

⇒ AB = AC (hai cạnh tương ứng)

Bài 2: Cho đường thẳng AB, trên hai nửa mặt phẳng đối nhau bờ là đoạn thẳng AB vẽ hai tia Ax ⊥ AB; By ⊥ BA. Trên Ax và By lần lượt lấy hai điểm C và D sao cho AC = BD. Gọi O là trung điểm của AB.

a) Chứng mình rằng: ΔAOC = ΔBOD

b) Chứng minh O là trung điểm của CD

Gợi ý đáp án

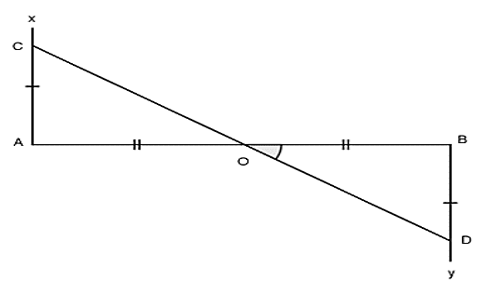
a) Xét ∆AOC và ∆BOD có:

OA = OB (gt)

$\widehat{OAC}=\widehat{OBD}={90}^0$ $\widehat{OAC}=\widehat{OBD}={90}^0$(gt)

AC = BD (gt)

Suy ra ∆AOC = ∆BOD (c - g - c)

b) Vì ∆AOC = ∆BOD (cmt)

$\Rightarrow\widehat{AOC}=\widehat{BOD};OC = OD$ $\Rightarrow\widehat{AOC}=\widehat{BOD};OC = OD$

Mà tia OC và OD là hai tia nằm khác phía đối với AB nên suy ra O, C, D thẳng hàng (hai tia đối của hai góc đối đỉnh hay O nằm giữa CD)

Ta có: O nằm giữa C và D nên OC = OD hay O là trung điểm của CD

c) Trường hợp 3: góc – cạnh – góc:

Bài 1: Cho ΔABC có $\widehat{B}=\widehat{C}$ $\widehat{B}=\widehat{C}$. Tia phân giác của góc B cắt AC tại D. Tia phân giác của góc C cắt AB tại E. So sánh độ dài đoạn thằng BD và CE.

Lời giải:

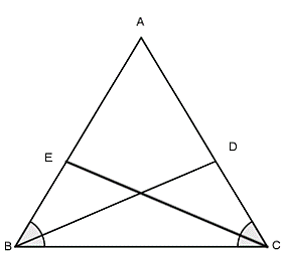
Xét ∆EBC và ∆DCB có:

$\widehat{EBC}=\widehat{DCB}$ $\widehat{EBC}=\widehat{DCB}$ (gt)

BC chung

$\widehat{ECB}=\widehat{DCB}$ $\widehat{ECB}=\widehat{DCB}$

Suy ra ∆EBC = ∆DCB (g - c - g)

Suy ra BD = CE (cặp cạnh tương ứng bằng nhau)

B. Bài tập tự luyện

Câu 1: Phát biểu các trường hợp bằng nhau của tam giác? Vẽ hình minh họa cho mỗi trường hợp?

Câu 2: Phát biểu các trường hợp bằng nhau của tam giác vuông? Vẽ hình minh họa cho mỗi trường hợp?

Câu 3: Phát biểu định lí một đường thẳng vuông góc với mọt trong hai đường thẳng song song? Ghi giả thiết kết luận? Vẽ hình minh họa?

Câu 4: Phát biểu định lí hai đường thẳng cùng vuông góc với một đường thẳng? Ghi giả thiết kết luận? Vẽ hình minh họa?

Câu 5: Phát biểu định lí ba đường thẳng song song? Ghi giả thiết kết luận? Vẽ hình minh?

Câu 6: Các em tự tìm hiểu những t/c, định lí nào có liêu quan đến các trường hợp bằng nhau của tam giác? Kể tên?

Sau khi nắm rõ các lý thuyết bên trên về những trường hợp bằng nhau của tam giác, mời các bạn cùng làm các bài tập ứng dụng dưới đây:

B. Bài tập tự luyện

Bài 1: Cho tam giác ABC; M là trung điểm BC; N là 1 điểm trong tam giác sao cho NB = NC.

Chứng minh: ∆NMB = ∆ NMC.

Bài 2. Cho ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng: ABE = ACE

Bài 3. Cho tam giác ABC có góc A = 40⁰ , AB = AC. Gọi M là trung điểm của BC. Tính các góc của tam giác AMB và tam giác AMC.

Bài 4. Cho tam giác ABC có AB = AC. D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE.

a. Chứng minh góc EAB = góc DAC.

b. Gọi M là trung điểm của BC. Chứng minh AM là phân giác của góc DAE.

c. Giả sử góc DAE = 60⁰. Tính các góc còn lại của tam giác DAE.

Bài 5. Cho tam giác ABC có góc A = 90⁰. Vẽ AD ⊥ AB (D, C nằm khác phía đối với AB) và AD = AB. Vẽ AE ⊥ AC (E, B nằm khác phía đối với AC) và AE = AC. Biết DE = BC. Tính góc BAC.

Bài 6. Cho ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng:

a. ∆ABE = ∆ACE

b. AE là đường trung trực của đoạn thẳng BC.

Bài 7. Cho ABC có AB < AC. Kẻ tia phân giác AD của góc BAC (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:

a. ∆BDF = ∆EDC.

b. BF = EC.

c. F, D, E thẳng hàng.

d. AD ⊥ FC

Bài 8. Cho góc nhọn xOy. Trên tia Ox, lấy 2 điểm A và C. Trên tia Oy lấy 2 điểm B và D sao cho OA = OB; OC = OD. (A nằm giữa O và C; B nằm giữa O và D).

a. Chứng minh ∆OAD = ∆OBC

b. So sánh 2 góc CAD và CBD.

Bài 9. Cho ΔABC vuông ở A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.

a. Chứng minh ΔABC = ΔABD

b. Trên tia đối của tia AB, lấy điểm M. Chứng minh ΔMBD = ΔMBC.

Bài 10. Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kì. Chứng minh:

a. ΔAOI = ΔBOI.

b. AB ⊥ OI.

Bài 11. Cho ΔABC, M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm E sao cho ME = MA.

a. Chứng minh AC // BE.

b. Gọi I là một điểm trên AC, K là một điểm trên EB sao cho AI = EK. Chứng minh 3 điểm I, M, K thẳng hàng.

Bài 12.Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BM = MD.

a/ Chứng minh : ΔABM = ΔCDM.

b/ Chứng minh : AB // CD

c/ Trên DC kéo dài lấy điểm N sao cho CD =CN (C ≠ N) chứng minh : BN // AC.

Bài 13: Cho tam giác ABC có AB = AC, trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho AM = AN. Gọi H là trung điểm của BC.

a/ Chứng minh : ΔABH = ΔACH.

b/ Gọi E là giao điểm của AH và NM. Chứng minh : ΔAME = ΔANE