Toán 7 Luyện tập chung trang 37 Giải Toán lớp 7 trang 37, 38 sách Kết nối tri thức - Tập 1

Giải bài tập Toán lớp 7 Luyện tập chung với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 7 Tập 1 Kết nối tri thức với cuộc sống trang 37, 38. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 7 chi tiết, còn giúp các em hệ thống lại toàn bộ kiến thức trọng tâm của Luyện tập chung Chương II: Số thực. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 7 Kết nối tri thức với cuộc sống trang 38 tập 1

Bài 2.19 trang 37 Toán 7 tập 1

Cho các phân số: $\frac{17}{80};\frac{611}{125};\frac{133}{91};\frac{9}{8}$

a) Phân số nào trong những phân số trên không viết được dưới dạng số thập phân hữu hạn?

b) Cho biết $\sqrt{2}=1,414213562$, hãy so sánh phân số tìm được trong câu a) với $\sqrt{2}$

Hướng dẫn giải:

- Các số thập phân chỉ gồm hữu hạn số sau dấu “,” được gọi là số thập phân hữu hạn.

- Các số thập phân vô hạn tuần hoàn có tính chất: Trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi.

Gợi ý đáp án:

a) Ta có:

$\frac{17}{80}=0,2125$
$\frac{611}{125}=4,888$
$\frac{133}{91}=1,(461538)$
$\frac{9}{8}=1,125$
=> Số không viết được dưới dạng số thập phân hữu hạn là: $\frac{133}{91}=1,(461538)$

b) Ta có: $\frac{133}{91}=1,(461538)$ mà $1,(461538)>1,414213562=>\frac{133}{91}>\sqrt{2}$

Bài 2.20 trang 37 Toán 7 tập 1

a. Viết các phân số sau dưới dạng số thập phân vô hạn tuần hoàn (dùng dấu ngoặc để chỉ rõ chu kì):$\frac{1}{9};\frac{1}{99}$. Em có nhận xét gì về kết quả nhận được?

b. Em hãy dự đoán dạng thập phân của $\frac{1}{999}$?

Hướng dẫn giải:

- Các số thập phân chỉ gồm hữu hạn số sau dấu “,” được gọi là số thập phân hữu hạn.

- Các số thập phân vô hạn tuần hoàn có tính chất: Trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi.

Gợi ý đáp án:

a. Viết dạng thập phân vô hạn tuần hoàn:

$\frac{1}{9}=0,(1)$

$\frac{1}{99}=0,(01)$

Nhận xét: Với phân số có dạng $\frac{1}{9\dots 9}$ thì dạng thập phân vô hạn tuần hoàn của nó sẽ là 0,(00..1) với n số 9 thì có n-1 số 0

b. Dự đoán dạng thập phân của $\frac{1}{999}=0,(001)$

Bài 2.21 trang 37 Toán 7 tập 1

Viết số $\frac{5}{9}$ và $\frac{5}{9}$ dưới dạng số thập phân vô hạn tuần hoàn.

Hướng dẫn giải:

- Các số thập phân chỉ gồm hữu hạn số sau dấu “,” được gọi là số thập phân hữu hạn.

- Các số thập phân vô hạn tuần hoàn có tính chất: Trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi.

Gợi ý đáp án:

$\begin{array}{rl}& \frac{5}{9}=0,(5)\\ & \frac{5}{9}=0,(05)\end{array}$

Bài 2.22 trang 37 Toán 7 tập 1

Nam vẽ một phần trục số trên vở ô li và đánh dấu ba điểm A, B,C như sau:

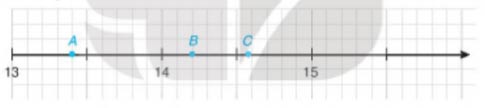
a. Hãy cho biết hai điểm A,B biểu diễn những số thập phân nào?

b. Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác 0,05.

Hướng dẫn giải:

- Các số thập phân chỉ gồm hữu hạn số sau dấu “,” được gọi là số thập phân hữu hạn.

- Các số thập phân vô hạn tuần hoàn có tính chất: Trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi.

Gợi ý đáp án:

a. Điểm A, B biểu diễn những số thập phân sau:

• Điểm A biểu diễn số 13,4
• Điểm B biểu diễn số 14,2

b. Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác 0,05, ta được 14,6.

Bài 2.23 trang 37 Toán 7 tập 1

Thay dấu “?” bằng chữ số thích hợp.

Hướng dẫn giải:

- Các số thập phân chỉ gồm hữu hạn số sau dấu “,” được gọi là số thập phân hữu hạn.

- Các số thập phân vô hạn tuần hoàn có tính chất: Trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi.

Gợi ý đáp án:

Bài 2.24 trang 37 Toán 7 tập 1

So sánh:

Hướng dẫn giải:

- Các số thập phân chỉ gồm hữu hạn số sau dấu “,” được gọi là số thập phân hữu hạn.

- Các số thập phân vô hạn tuần hoàn có tính chất: Trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi.

Gợi ý đáp án:

a. Ta có: 12,(24) = 12,2424... Vì so sánh số ở hàng phần chục ta có 4<6 nên 12,(24)< 12,26

b. Vì so sánh ở hàng chục ta có 3 > 2 nên 31,3(5) > 29,9(8)

Bài 2.25 trang 37 Toán 7 tập 1

Tính:

Hướng dẫn giải:

- Căn bậc hai số học của một số a không âm, kí hiệu là $\sqrt{a}$, là số x không âm sao cho $x^2=a$

- Căn bậc hai số học của một số tự nhiên không chính phương luôn là số số vô tỉ.

- Diện tích hình vuông bằng bình phương độ dài cạnh.

Gợi ý đáp án:

a. $\sqrt{1}=1$

b. $\sqrt{1+2+1}=\sqrt{4}=2$

c. $\sqrt{1+2+3+2+1}=\sqrt{9}=3$

Bài 2.26 trang 37 Toán 7 tập 1

Tính:

Gợi ý đáp án: