Toán 7 Bài 6: Số vô tỉ. Căn bậc hai số học Giải Toán lớp 7 trang 29 - Tập 1 sách Kết nối tri thức với cuộc sống

Bài trước

Mục lục

Bài sau

Giải Toán lớp 7 bài 6: Số vô tỉ. Căn bậc hai số học bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 7 Tập 1 Kết nối tri thức với cuộc sống trang 29, 30, 31, 32.

Lời giải Toán 7 Bài 6 Kết nối tri thức trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 7, từ đó học tốt môn Toán lớp 7 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài 6 Chương II - Số thực. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 7 bài 6: Số vô tỉ. Căn bậc hai số học sách Kết nối tri thức với cuộc sống

Giải Toán 7 Kết nối tri thức với cuộc sống tập 1 bài 6 - Luyện tập
- Luyện tập 1
- Luyện tập 2
Giải Toán 7 Kết nối tri thức với cuộc sống trang 32 tập 1

Giải Toán 7 Kết nối tri thức với cuộc sống tập 1 bài 6 - Luyện tập

Luyện tập 1

Tính:

a) $\sqrt {16}$ $\sqrt {16}$

b) $\sqrt {81}$ $\sqrt {81}$

c) $\sqrt {{{2021}^2}}$ $\sqrt {{{2021}^2}}$

Gợi ý đáp án:

a) Ta có: 16 = 4², 4 > 0 => $\sqrt {16} = 4$ $\sqrt {16} = 4$

Vậy căn bậc hai số học của 16 là 4

b) Ta có: 81 = 9², 9 > 0 => $\sqrt {81} = 9$ $\sqrt {81} = 9$

Vậy căn bậc hai số học của 81 là 9

c) Ta có: 2021 > 0 => $\sqrt {{{2021}^2}} = 2021$ $\sqrt {{{2021}^2}} = 2021$

Vậy căn bậc hai số học của 2021² là 2021.

Luyện tập 2

Sử dụng máy tính cầm tay tìm căn bậc hai số học của các số sau (làm tròn các kết quả với độ chính các 0,005, nếu cần)

a) $\sqrt {15}$ $\sqrt {15}$

b) $\sqrt {2,56}$ $\sqrt {2,56}$

c) $\sqrt {17256}$ $\sqrt {17256}$

d) $\sqrt {793881}$ $\sqrt {793881}$

Gợi ý đáp án:

Phép tính	Ấn các phím	Kết quả	Kết quả làm tròn
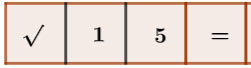$\sqrt {15}$ $\sqrt {15}$		3,87298334621	3,87
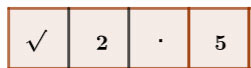$\sqrt {2,56}$ $\sqrt {2,56}$		1,6	1,6
$\sqrt {17256}$ $\sqrt {17256}$		131,36209498938	131,36
$\sqrt {793881}$ $\sqrt {793881}$		891	891

Giải Toán 7 Kết nối tri thức với cuộc sống trang 32 tập 1

Bài 2.6

Cho biết ${153^2} = 23409$ ${153^2} = 23409$. Hãy tính $\sqrt {23409}$ $\sqrt {23409}$

Gợi ý đáp án:

$\sqrt {23409} = 153$ $\sqrt {23409} = 153$

Bài 2.7

Từ các số là bình phương cảu 12 số tự nhiên đầu tiên, em hãy tìm căn bậc hai số học của các số sau:

a) 9;

c) 81;

b) 16;

d) 121

Gợi ý đáp án:

a) Vì ${3^2} = 9$ ${3^2} = 9$ nên $\sqrt 9 = 3$ $\sqrt 9 = 3$

b) Vì ${4^2} = 16$ ${4^2} = 16$ nên $\sqrt {16} = 4$ $\sqrt {16} = 4$

c) Vì ${9^2} = 81$ ${9^2} = 81$ nên $\sqrt {81} = 9$ $\sqrt {81} = 9$

d) Vì ${11^2} = 121$ ${11^2} = 121$ nên $\sqrt {121} = 11$ $\sqrt {121} = 11$

Bài 2.8

Khi tìm căn bậc hai số học của một số tự nhiên ta thường phân tích số đó ra thừa số nguyên tố. Chẳng hạn:

Vì $324 = {2^2}{.3^4} = {({2.3^2})^2} = {18^2}$ $324 = {2^2}{.3^4} = {({2.3^2})^2} = {18^2}$ nên $\sqrt {324} = 18$ $\sqrt {324} = 18$

Tính căn bậc hai số học của 129 600.

Gợi ý đáp án:

Ta có: $129{\rm{ }}600 = {2^6}{.3^4}{.5^2} = {({2^3}{.3^2}.5)^2} = {360^2}$ $129{\rm{ }}600 = {2^6}{.3^4}{.5^2} = {({2^3}{.3^2}.5)^2} = {360^2}$ nên $\sqrt {129600} = 360$ $\sqrt {129600} = 360$

Bài 2.9

Tính độ dài các cạnh của hình vuông có diện tích bằng:

a) 81 dm²;

b) 3 600 m²;

c) 1 ha

Gợi ý đáp án:

a) Độ dài các cạnh của hình vuông là: $\sqrt {81} = 9 (dm)$ $\sqrt {81} = 9 (dm)$

b) Độ dài các cạnh của hình vuông là: $\sqrt {3600} = 60 (m)$ $\sqrt {3600} = 60 (m)$

c) Đổi 1 ha = 10 000 m²

Độ dài các cạnh của hình vuông là: $\sqrt {10000} = 100 (m)$ $\sqrt {10000} = 100 (m)$

Chú ý: Câu c cần đổi đơn vị trước khi tìm căn bậc hai số học.

Bài 2.10

Sử dụng máy tính cầm tay tìm căn bậc hai số học của các số sau rồi làm tròn các kết quả với độ chính xác 0,005.

a) 3; b) 41; c) 2 021

Gợi ý đáp án:

Làm tròn các kết quả với độ chính xác 0,005 tức là làm tròn đến hàng phần trăm.

$\begin{array}{l}a)\sqrt 3 = 1,73205.... \approx 1,73\\b)\sqrt {41} = 6,40312.... \approx 6,40\\c)\sqrt {2021} = 44,95553.... \approx 44,96\end{array}$ $\begin{array}{l}a)\sqrt 3 = 1,73205.... \approx 1,73\\b)\sqrt {41} = 6,40312.... \approx 6,40\\c)\sqrt {2021} = 44,95553.... \approx 44,96\end{array}$

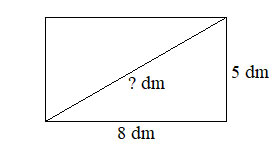
Bài 2.11

Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài là 8 dm và chiều rộng là 5 dm. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu đềximét (làm tròn kết quả đến hàng phần mười)?

Bài 2.11

Gợi ý đáp án:

Ta có: Bình phương độ dài đường chéo của một hình chữ nhật là: ${5^2} + {8^2} = 25 + 64 = 89$ ${5^2} + {8^2} = 25 + 64 = 89$

Độ dài đường chéo của một hình chữ nhật là: $\sqrt {89} = 9,43398...(dm)$ $\sqrt {89} = 9,43398...(dm)$

Làm tròn kết quả này ta được: 9,4 dm

Chú ý: Độ dài đường chéo của một hình chữ nhật bằng căn bậc hai số học của tổng các bình phương độ dài hai cạnh của nó

Bài 2.12

Để lát một mảnh sân hình vuông có diện tích 100m², người ta cần dùng bao nhiêu viên gạch hình vuông có cạnh dài 50 cm (coi các mạch ghép là không đáng kể)?

Gợi ý đáp án:

Diện tích 1 viên gạch là: 50² = 2500 (cm²) = 0,25 m².

Số viên gạch cần là: 100 : 0,25 = 400 (viên)

Luyện tập 1

Chia sẻ bởi: