Giải Toán 8 Bài 4: Quy đồng mẫu thức nhiều phân thức Giải SGK Toán 8 Tập 1 (trang 43, 44)

Giải bài tập SGK Toán 8 Tập 1 trang 43, 44 giúp các em học sinh lớp 8 xem gợi ý giải các bài tập của Bài 4: Quy đồng mẫu thức nhiều phân thức. Thông qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 4 Chương 2 phần Đại số trong sách giáo khoa Toán 8 Tập 1.

Giải bài tập Toán 8 trang 43 tập 1

Bài 14 (trang 43 SGK Toán 8 Tập 1)

Quy đồng mẫu thức các phân thức sau:

Gợi ý đáp án:

a) Mẫu thức chung: \(12{x^5}{y^4}\)

Nhân tử phụ:

\(12{x^5}{y^4}:{\rm{ }}{x^5}{y^3} = {\rm{ }}12y\)

\(12{\rm{ }}{x^5}{y^4}:{\rm{ }}12{x^3}{y^4} = {\rm{ }}x^2\)

Quy đồng:

\(\dfrac{5}{x^{5}y^{3}}= \dfrac{5.12y}{x^{5}y^{3}.12y}= \dfrac{60y}{12x^{5}y^{4}}\)

\(\dfrac{7}{12x^{3}y^{4}}= \dfrac{7x^{2}}{12x^{3}y^{4}.x^{2}}= \dfrac{7x^{2}}{12x^{5}y^{4}}\)

b) Mẫu thức chung: \(60{x^4}{y^5}\)

Nhân tử phụ: \(60{x^4}{y^5}:{\rm{ }}15{x^3}{y^5} = {\rm{ }}4x\)

\(60{x^4}{y^5}:{\rm{ }}12{x^4}{y^2} = {\rm{ }}5{y^3}\)

Quy đồng:

\(\dfrac{4}{15x^{3}y^{5}}= \dfrac{4.4x}{15x^{3}y^{{5}}.4x}= \dfrac{16x}{60x^{4}y^{5}}\)

\(\dfrac{11}{12x^{4}y^{2}}= \dfrac{11.5y^{3}}{12x^{4}y^{2}.5y^{3}}= \dfrac{55y^{3}}{60x^{4}y^{5}}\)

Bài 15 (trang 43 SGK Toán 8 Tập 1)

Quy đồng mẫu các phân thức sau:

Gợi ý đáp án:

a) Tìm mẫu thức chung:

\(2x + 6 = 2(x + 3)\)

\(x^2- 9 = (x -3)(x + 3)\)

Mẫu thức chung là: \(2(x - 3)(x + 3)\)

Nhân tử phụ thứ nhất là: (x-3)

Nhân tử phụ thứ hai là: 2

Quy đồng:

\(\dfrac{5}{2x +6}=\dfrac{5}{2(x+3)}=\dfrac{5(x-3)}{2(x-3)(x+3)}\)

\(\dfrac{3}{x^{2}-9}= \dfrac{3}{(x-3)(x+3)}= \dfrac{3.2}{2(x-3)(x+3)}=\dfrac{6}{2(x-3)(x+3)}\)

b) Tìm mẫu thức chung:

\({x^2}-{\rm{ }}8x{\rm{ }} + {\rm{ }}16{\rm{ }} = {x^2} - 2.x.4 + {4^2}= {\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}4} \right)^2}\)

\(3x^2– 12x = 3x(x - 4)\)

Mẫu thức chung là: \(3x(x - 4)^2\)

Nhân tử phụ thứ nhất là: 3x

Nhân tử phụ thứ hai là: (x-4)

Quy đồng:

\(\dfrac{2x}{x^{2}-8x+16}=\dfrac{2x}{(x-4)^{2}}=\dfrac{2x.3x}{3x(x-4)^{2}}=\dfrac{6x^{2}}{3x(x-4)^{2}}\)

\(\dfrac{x}{3x^{2}-12}=\dfrac{x}{3x(x-4)}=\dfrac{x(x-4)}{3x(x-4)^{2}}\)

Bài 16 (trang 43 SGK Toán 8 Tập 1)

Quy đồng mẫu thức các phân thức sau (có thể áp dụng quy tắc đổi dấu đối với một phân thức để tìm mẫu thức chung thuận tiện hơn):

Gợi ý đáp án:

a) Tìm mẫu thức chung:

\({x^3} - 1 = \left( {x - 1} \right)({x^2} + {\rm{ }}x + 1)\)

Nên mẫu thức chung là: \(\left( {x - 1} \right)({x^2} + {\rm{ }}x + 1)\)

Nhân tử phụ thứ nhất là 1

Nhân tử phụ thứ hai là (x-1)

Nhân tử phụ thứ ba là \(\left( {x - 1} \right)({x^2} + {\rm{ }}x + 1)\)

Quy đồng:

\(\dfrac{4x^{2}-3x+5}{x^{3}-1}=\dfrac{4x^{2}-3x+5}{(x-1)(x^{2}+x+1)}\)

\(\dfrac{1-2x}{x^{2}+x+1}=\dfrac{(x-1)(1-2x)}{(x-1)(x^{2}+x+1)}\)

\(-2 = \dfrac{-2(x^{3}-1)}{(x-1)(x^{2}+x+1)}\)

b) Tìm mẫu thức chung:

\(x+ 2=x+2\)

\(2x - 4 = 2(x - 2)\)

\(6 - 3x = 3(2 - x) = -3(x -2)\)

Mẫu thức chung là: 6(x - 2)(x + 2)

Nhân tử phụ thứ nhất là 6(x-2)

Nhân tử phụ thứ hai là 3(x+2)

Nhân tử phụ thứ ba là -2(x+2)

Quy đồng:

\(\dfrac{10}{x+2}= \dfrac{10.6.(x-2)}{6(x-2)(x+2)}=\dfrac{60(x-2)}{6(x-2)(x+2)}\)

\(\dfrac{5}{2x-4}=\dfrac{5}{2(x-2)}=\dfrac{5.3(x+2)}{2(x-2).3(x+2)}=\dfrac{15(x+2)}{6(x-2)(x+2)}\)

\(\dfrac{1}{6-3x}=\dfrac{1}{-3(x-2)}=\dfrac{-2(x+2)}{-3(x-2).[-2(x+2)]}=\dfrac{-2(x+2)}{6(x-2)(x+2)}\)

Bài 17 (trang 43 SGK Toán 8 Tập 1)

Đố. Cho hai phân thức: \(\dfrac{5x^{2}}{x^{3}-6x^{2}},\dfrac{3x^{2}+18x}{x^{2}-36}\)

Khi quy đồng mẫu thức, bạn Tuấn đã chọn \(MTC = {x^2}\left( {x - 6} \right)\left( {x + 6} \right)\) còn bạn Lan bảo rằng: "Quá đơn giản! MTC = x - 6". Đố em biết bạn nào chọn đúng?

Gợi ý đáp án:

Cách làm của bạn Tuấn:

Bạn Tuấn trực tiếp đi tìm mẫu thức chung theo quy tắc:

\(\begin{array}{l} {x^3} - 6{{\rm{x}}^2} = {x^2}\left( {x - 6} \right)\\ {x^2} - 36 =x^2-6^2= \left( {x - 6} \right)\left( {x + 6} \right)\\ MTC = {x^2}\left( {x - 6} \right)\left( {x + 6} \right) \end{array}\)

Do đó bạn Tuấn làm đúng.

Cách làm của bạn Lan:

Bạn Lan rút gọn phân thức trước khi đi tìm mẫu thức chung:

\(\begin{array}{l} \dfrac{{5{{\rm{x}}^2}}}{{{x^3} - 6{{\rm{x}}^2}}} = \dfrac{{5{{\rm{x}}^2}}}{{{x^2}\left( {x - 6} \right)}} = \dfrac{5}{{x - 6}}\\ \dfrac{{3{{\rm{x}}^2} + 18{\rm{x}}}}{{{x^2} - 36}} = \dfrac{{3{\rm{x}}\left( {x + 6} \right)}}{{\left( {x - 6} \right)\left( {x + 6} \right)}} = \dfrac{{3{\rm{x}}}}{{x - 6}} \end{array}\)

Do đó MTC = x - 6. Vậy bạn Lan làm đúng.

Vậy cả hai bạn đều làm đúng. Bạn Tuấn đã tìm MTC theo đúng qui tắc. Bạn Lan thì rút gọn các phân thức trước khi tìm MTC.

* Nhận xét: Ta nên rút gọn hoàn toàn các phân thức trước khi quy đồng để việc quy đồng ngắn gọn hơn.

Giải bài tập Toán 8 trang 43, 44 tập 1: Luyện tập

Bài 18 (trang 43 SGK Toán 8 Tập 1)

Quy đồng mẫu thức hai phân thức:

a) \(\dfrac{{3x}}{{2x + 4}}\) và \(\dfrac{{x + 3}}{{{x^2} - 4}}\)

b) \(\dfrac{{x + 5}}{{{x^2} + 4x + 4}}\) và \(\dfrac{x}{{3x + 6}}\)

Gợi ý đáp án:

a) + Phân tích mẫu thức thành nhân tử để tìm mẫu thức chung

2x + 4 =2(x+2)

\({x^2} - 4 = \left( {x - 2} \right)\left( {x + 2} \right)\)

\(⇒ MTC = 2\left( {x - 2} \right)\left( {x + 2} \right) = 2\left( {{x^2} - 4} \right)\)

+ Nhân tử phụ:

\(2\left( {x - 2} \right)\left( {x + 2} \right) :2(x+2)=x-2\)

\(2\left( {x - 2} \right)\left( {x + 2} \right) :(x-2)(x+2)=2\)

+ Quy đồng:

\(\dfrac{{3x}}{{2x + 4}} = \dfrac{{3x\left( {x - 2} \right)}}{{2\left( {x + 2} \right)\left( {x - 2} \right)}} = \dfrac{{3x\left( {x - 2} \right)}}{{2\left( {{x^2} - 4} \right)}}\)

\(\dfrac{{x + 3}}{{{x^2} - 4}} = \dfrac{{\left( {x + 3} \right).2}}{{\left( {x - 2} \right)\left( {x + 2} \right).2}} = \dfrac{{2\left( {x + 3} \right)}}{{2\left( {{x^2} - 4} \right)}}\)

b) + Phân tích mẫu thức thành nhân tử để tìm mẫu thức chung

\({x^2} + 4x + 4 = {x^2} + 2.x.2 + {2^2}= {\left( {x + 2} \right)^2}\)

\(3x + 6 = 3\left( {x + 2} \right)\)

Nên \(MTC = 3{\left( {x + 2} \right)^2}\)

+ Nhân tử phụ:

\(3{\left( {x + 2} \right)^2}:(x+2)^2=3\)

\(3{\left( {x + 2} \right)^2}:3(x+2)=x+2\)

+ Quy đồng:

\(\dfrac{{x + 5}}{{{x^2} + 4x + 4}} = \dfrac{{\left( {x + 5} \right).3}}{{{{\left( {x + 2} \right)}^2}.3}} = \dfrac{{3\left( {x + 5} \right)}}{{3{{\left( {x + 2} \right)}^2}}}\)

\(\dfrac{x}{{3x + 6}} = \dfrac{{x.\left( {x + 2} \right)}}{{3\left( {x + 2} \right).\left( {x + 2} \right)}} = \dfrac{{x\left( {x + 2} \right)}}{{3{{\left( {x + 2} \right)}^2}}}\)

Bài 19 (trang 43 SGK Toán 8 Tập 1)

Quy đồng mẫu thức các phân thức sau:

Gợi ý đáp án:

a) + Phân tích mẫu thức thành nhân tử để tìm MTC

2x – x^2 = x.(2 – x)

\(MTC = x\left( {2 - x} \right)\left( {2 + x} \right)\)

+ Nhân tử phụ :

\(x.(2-x)(x+2) : (x + 2) = x.(2 – x)\)

\(x(2-x)(x+2) : x(2 – x) = x + 2\)

+ Quy đồng:

\(\dfrac{1}{{x + 2}} = \dfrac{1}{{2 + x}} = \dfrac{{x\left( {2 - x} \right)}}{{x\left( {2 - x} \right)\left( {2 + x} \right)}} = \dfrac{{2x - {x^2}}}{{x(2 - x)(2 + x)}}\)

\(\dfrac{8}{{2x - {x^2}}} = \dfrac{{8.(2 + x)}}{{x(2 - x)(2 + x)}} = \dfrac{{16 + 8x}}{{x(2 - x)(2 + x)}}\)

b) \(MTC = {x^2} - 1\)

Quy đồng:

\({x^2} + 1 = \dfrac{{{x^2} + 1}}{1} = \dfrac{{\left( {{x^2} + 1} \right)\left( {{x^2} - 1} \right)}}{{{x^2} - 1}} = \dfrac{{{x^4} - 1}}{{{x^2} - 1}}\)

\(\dfrac{{{x^4}}}{{{x^2} - 1}}\) giữ nguyên.

c) Ta có: \(\dfrac{x}{{{y^2} - xy}} = \dfrac{-x}{{xy-y^2}}\)

+ Phân tích mẫu thức thành nhân tử:

\({x^3} - 3{x^2}y + 3x{y^2} - {y^3} = {\left( {x - y} \right)^3}\)

\(xy-{y^2} = y\left( {x - y} \right)\)

\(MTC = y{\left( {x - y} \right)^3}\)

+ Nhân tử phụ:

\(y(x – y)^3 : (x – y)^3 = y\)

\(y(x – y)^3 : y(x – y) = (x – y)^2\)

+ Quy đồng mẫu thức:

\(\dfrac{{{x^3}}}{{{x^3} - 3{x^2}y + 3x{y^2} - {y^3}}} = \dfrac{{{x^3}}}{{{{\left( {x - y} \right)}^3}}} = \dfrac{{{x^3}y}}{{y{{\left( {x - y} \right)}^3}}}\)

\(\dfrac{x}{{{y^2} - xy}} = \dfrac{-x}{{xy-y^2}} = \dfrac{{ - x}}{{y\left( {x - y} \right)}} = \dfrac{{ - x{{\left( {x - y} \right)}^2}}}{{y(x-y).{{(x - y)}^2}}}= \dfrac{{ - x{{\left( {x - y} \right)}^2}}}{{y{{(x - y)}^3}}}\)

Bài 20 (trang 44 SGK Toán 8 Tập 1)

Cho hai phân thức:

\(\dfrac{1}{{{x^2} + 3x - 10}},\;\dfrac{x}{{{x^2} + 7x + 10}}\)

Không dùng cách phân tích các mẫu thức thành nhân tử, hãy chứng tỏ rằng có thể quy đồng mẫu thức hai phân thức này với mẫu thức chung là: \({x^3} + 5{x^2} - 4x - 20\).

Gợi ý đáp án:

Để chứng tỏ rằng có thể chọn đa thức \({x^3} + 5{x^2} - 4x - 20\) làm mẫu thức chung ta chỉ cần chứng tỏ rằng nó chia hết cho mẫu thức của mỗi phân thức đã cho.

Ta xét các phép chia:

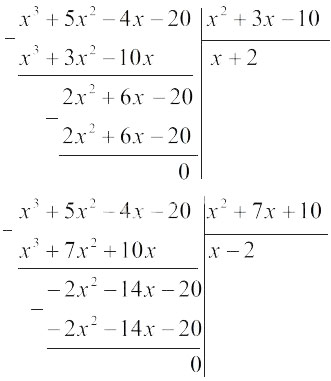
Do đó:

\(\begin{array}{l} {x^3} + 5{{\rm{x}}^2} - 4{\rm{x}} - 20\\ = \left( {{x^2} + 3{\rm{x}} - 10} \right)\left( {x + 2} \right)\\ = \left( {{x^2} + 7{\rm{x + }}10} \right)\left( {x - 2} \right) \end{array}\)

+) \(MTC = {x^3} + 5{x^2} - 4x - 20\)

Nhân tử phụ của mẫu thứ nhất là: (x+2)

Nhân tử phụ của mẫu thứ hai là: (x-2)

+) Quy đồng mẫu thức:

\(\dfrac{1}{{{x^2} + 3x - 10}} = \dfrac{{1.\left( {x + 2} \right)}}{{\left( {{x^2} + 3x - 10} \right)\left( {x + 2} \right)}}= \dfrac{{x + 2}}{{{x^3} + 5{x^2} - 4x - 20}}\)

\(\dfrac{x}{{{x^2} + 7x + 10}}= \dfrac{{x\left( {x - 2} \right)}}{{\left( {{x^2} + 7x + 10} \right)\left( {x - 2} \right)}}= \dfrac{{{x^2} - 2x}}{{{x^3} + 5{x^2} - 4x - 20}}\)