Giải Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp Giải SGK Toán 8 Tập 1 (trang 31, 32)

Giải bài tập SGK Toán 8 Tập 1 trang 31, 32 giúp các em học sinh lớp 8 xem gợi ý giải các bài tập của Bài 12: Chia đa thức một biến đã sắp xếp. Thông qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 12 Chương 1 phần Đại số trong sách giáo khoa Toán 8 Tập 1.

Giải bài tập Toán  8 trang 31 tập 1

Bài 67 (trang 31 SGK Toán 8 Tập 1)

Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia:

Gợi ý đáp án:

a) x³ – 7x + 3 – x² = x³ – x² – 7x + 3

Thực hiện phép chia:

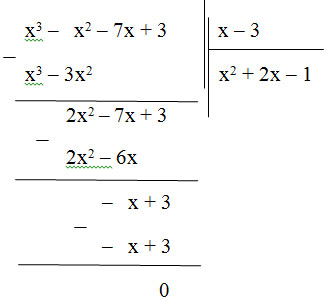
Vậy (x³ – x² – 7x + 3) : (x – 3) = x² + 2x – 1

b) 2x⁴ – 3x³ – 3x² – 2 + 6x = 2x⁴ – 3x³ – 3x² + 6x – 2

Thực hiện phép chia:

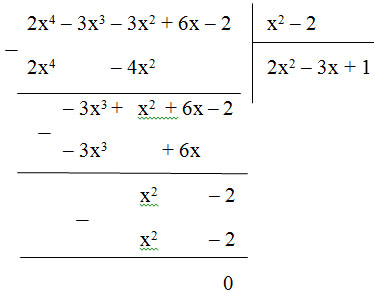
Vậy (2x⁴ – 3x³ – 3x² + 6x – 2) : (x² – 2) = 2x² – 3x + 1.

Bài 68 (trang 31 SGK Toán 8 Tập 1)

Áp dụng hằng đẳng thức đáng nhớ để thực hiện phép chia:

Gợi ý đáp án:

a) (x² + 2xy + y²) : (x + y) = (x + y)² : (x + y) = x + y.

b) (125x³ + 1) : (5x + 1) = [(5x)³ + 1] : (5x + 1)

= (5x)² – 5x + 1 = 25x² – 5x + 1.

c) (x² – 2xy + y²) : (y – x) = (x – y)² : [-(x – y)] = – (x – y) = y – x

Hoặc (x² – 2xy + y²) : (y – x) = (y² – 2xy + x²) : (y – x)

= (y – x)² : (y – x) = y – x.

Bài 69 (trang 31 SGK Toán 8 Tập 1)

Cho hai đa thức: A = 3x⁴ + x³ + 6x – 5 và B = x² + 1. Tìm dư R trong phép chia A cho B rồi viết A dưới dạng A = B.Q + R

Gợi ý đáp án:

Thực hiện phép chia ta có:

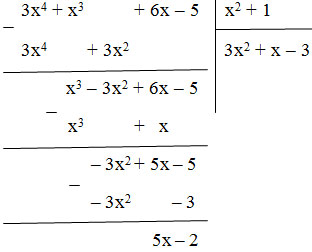
Vậy 3x⁴ + x³ + 6x – 5 = (x² + 1).(3x² + x – 3) + 5x – 2.

Giải bài tập Toán 8 trang 32 tập 1: Luyện tập

Bài 70 (trang 32 SGK Toán 8 Tập 1)

Làm tính chia:

Gợi ý đáp án:

a) (25x⁵ – 5x⁴ + 10x²) : 5x² = (25x⁵ : 5x² ) – (5x⁴ : 5x² ) + (10x² : 5x²) = 5x3 – x2 + 2

b) (15x³y² – 6x²y – 3x²y²) : 6x²y

= (15x³y² : 6x²y) + (– 6x²y : 6x²y) + (– 3x²y² : 6x²y)

= \(\frac{15}{6}\)xy – 1 – \(\frac{3}{6}\)y = \(\frac{5}{2}\)xy – \(\frac{1}{2}\)y – 1.

Bài 71 (trang 32 SGK Toán 8 Tập 1)

Không thực hiện phép chia, hãy xét xem đa thức A có chia hết cho đa thức B hay không.

a) A = 15x⁴ – 8x³ + x²

B = \(\frac{1}{2}\)x²

b) A = x² – 2x + 1

B = 1 – x

Gợi ý đáp án:

a) Ta có 15x⁴ ; 8x³ ; x² chia hết cho 1/2x² nên đa thức A chia hết cho B.

b) A chia hết cho B, vì x² – 2x + 1 = (1 – x)², chia hết cho 1 – x

Bài 72 (trang 32 SGK Toán 8 Tập 1)

Làm tính chia:

(2x⁴ + x³ – 3x² + 5x – 2) : (x² – x + 1).

Gợi ý đáp án:

Thực hiện phép chia:

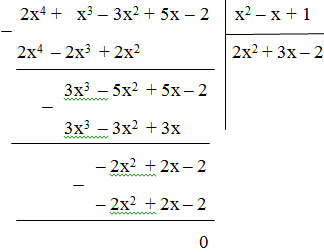
Vậy (2x⁴ + x³ – 3x² + 5x – 2) : (x² – x + 1) = 2x² + 3x - 2

Bài 73 (trang 32 SGK Toán 8 Tập 1)

Tính nhanh:

Gợi ý đáp án:

a) (4x² – 9y²) : (2x – 3y)

(Sử dụng HĐT để phân tích số bị chia thành tích)

= [(2x)² – (3y)²] : (2x – 3y)

(Xuất hiện hằng đẳng thức (3))

= (2x – 3y)(2x + 3y) : (2x – 3y)

= 2x + 3y.

b) (27x³ – 1) : (3x – 1)

(Sử dụng HĐT để phân tích số bị chia thành tích)

= [(3x)³ – 1] : (3x – 1)

(Xuất hiện hằng đẳng thức (7))

= (3x – 1).[(3x)² + 3x.1 + 1²] : (3x – 1)

= (3x – 1).(9x² + 3x + 1) : (3x – 1)

= 9x² + 3x + 1

c) (8x³ + 1) : (4x² – 2x + 1)

(Sử dụng HĐT để phân tích số bị chia thành tích)

= [(2x)³ + 1] : (4x² – 2x + 1)

(Xuất hiện HĐT (6))

= (2x + 1).[(2x)² - 2x.1 + 1²] : (4x² – 2x + 1)

= (2x + 1).(4x² - 2x + 1) : (4x² – 2x + 1)

= 2x + 1.

d) (x² – 3x + xy – 3y) : (x + y)

(Nhóm hạng tử để phân tích số bị chia thành tích)

= [(x² – 3x) + (xy – 3y)] : (x + y)

= [x.(x – 3) + y.(x – 3)] : (x + y)

= (x + y).(x – 3) : (x + y)

= x – 3.

Bài 74 (trang 32 SGK Toán 8 Tập 1)

Tìm số a để đa thức 2x³ – 3x² + x + a chia hết cho đa thức x + 2.

Gợi ý đáp án:

Cách 1: Thực hiện phép chia:

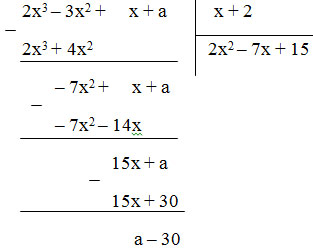
2x³ – 3x² + x + a chia hết cho x + 2

⇔ số dư = a – 30 = 0

⇔ a = 30.

Cách 2: Phân tích 2x³ – 3x² + x + a thành nhân tử có chứa x + 2.

2x³ – 3x² + x + a

= 2x³ + 4x² – 7x² – 14x + 15x + 30 + a – 30

(Tách -3x² = 4x² – 7x²; x = -14x + 15x)

= 2x²(x + 2) – 7x(x + 2) + 15(x + 2) + a – 30

= (2x² – 7x + 15)(x + 2) + a – 30

2x³ – 3x² + x + a chia hết cho x + 2 ⇔ a – 30 = 0 ⇔ a = 30.