Toán 8 Bài 10: Tứ giác Giải Toán 8 Kết nối tri thức trang 48, 49, 50, 51

Giải Toán lớp 8 trang 48, 49, 50, 51 sách tập 1 giúp Kết nối tri thức các em học sinh lớp 8 tham khảo, dễ dàng xem gợi ý giải các bài tập Bài 10: Tứ giác của Chương III: Tứ giác.

Giải SGK Toán 8 KNTT tập 1 trang 48 - 51 được biên soạn chi tiết, bám sát nội dung trong sách giáo khoa. Đồng thời, cũng giúp thầy cô tham khảo để soạn giáo án cho học sinh của mình theo chương trình mới. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Phần Luyện tập

Luyện tập 1 trang 49 Toán 8 Tập 1

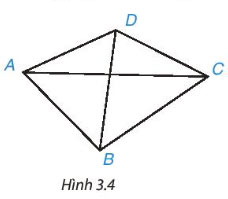
Quan sát tứ giác ABCD trong Hình 3.4.

- Hai đỉnh không cùng thuộc một cạnh gọi là hai đỉnh đối nhau. Đoạn thẳng nối hai đỉnh đối nhau là một đường chéo, chẳng hạn AC là một đường chéo. Kể tên đường chéo còn lại.

- Cặp cạnh AB, CD là cặp cạnh đối. Chỉ ra cặp cạnh đối còn lại.

- Cặp góc A, C là cặp góc đối. Hãy kể tên cặp góc đối còn lại.

Bài giải:

- Đường chéo còn lại là: BD

- Cặp cạnh đối còn lại: AD và BC

- Cặp góc đối còn lại: B và D

Luyện tập 1 trang 50 Toán 8 Tập 1

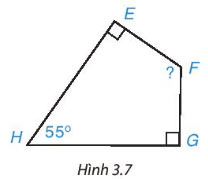
Cho tứ giác EFGH như Hình 3.7. Hãy tính góc F. 

Bài giải:

Xét tứ giác HEFG có: \(\widehat{H}+\widehat{E}+\widehat{F}+\widehat{G} =360^{\circ}\) (Tổng các góc của một tứ giác bằng 360^o)

\(\widehat{F}=360^{\circ}-\widehat{E}-\widehat{G}-\widehat{H}\)

\(=360^{\circ}-90^{\circ}-90^{\circ}-55^{\circ}=125^{\circ}\)

Vậy \(\widehat{F}=125^{\circ}\)

Phần Vận dụng

Giải bài toán mở đầu.

Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b.

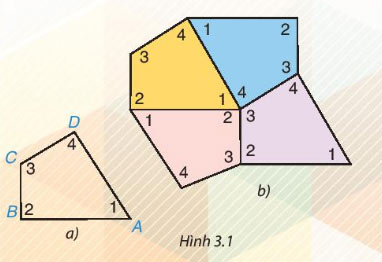
- Em có thể ghép bốn tứ giác khít nhau như vậy không?

- Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo của bốn góc đó.

Lời giải:

- Dựa vào hình 3.1 ta thấy có thể ghép bốn tứ giác khít nhau như vây.

- Bốn góc tại điểm chung của bốn tứ giác là bốn góc của một tứ giác.

Vậy tổng số đo của bốn góc đó là: 360^o. (định lí tổng bốn góc trong một tứ giác)

Phần Bài tập

Bài 3.1 trang 51 Toán 8 Tập 1

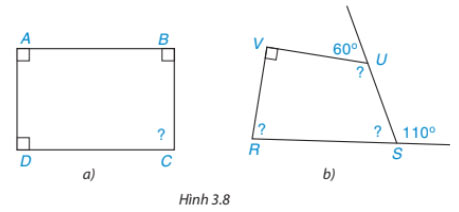
Tính góc chưa biết của các tứ giác trong Hình 3.8

Bài giải:

a) \(\widehat{C}=360^{\circ}-\widehat{A}+\widehat{B}-\widehat{D}\)

\(=360^{\circ}-90^{\circ}-90^{\circ}-90^{\circ}=90^{\circ}\)

b) \(\widehat{U}=180^{\circ}-60^{\circ}=120^{\circ}\)

\(\widehat{S}=180^{\circ}-110^{\circ}=70^{\circ}\)

\(\widehat{R}=360^{\circ}-\widehat{V}+\widehat{S}-\widehat{R}\)

\(=360^{\circ}-90^{\circ}-120^{\circ}-70^{\circ}=80^{\circ}\)

Bài 3.2 trang 51 Toán 8 Tập 1

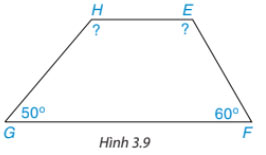
Tính góc chưa biết củ tứ giác trong Hình 3.9. Biết \(\widehat{H}=\widehat{E}+10^{\circ}\)

Bài giải:

Ta có: \(\widehat{H}+\widehat{E}=360^{\circ}-\widehat{G}+\widehat{F}\)

\(=360^{\circ}-50^{\circ}-60^{\circ}=150^{\circ}\) (1)

Lại có: \(\widehat{H}=\widehat{E}+10^{\circ} \Rightarrow \widehat{H}-\widehat{E}=10^{\circ}\) (2)

Từ (1) và (2) suy ra \(\widehat{H}=80^{\circ}; \widehat{E}=70^{\circ}\)

Bài 3.3 trang 51 Toán 8 Tập 1

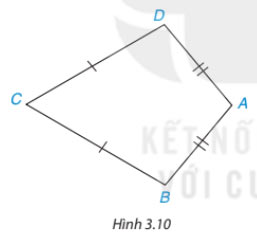
Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình "cái diều".

a) Chứng minh rằng AC là đường trung trực của đoạn BD

b) Tính các góc B, D biết rằng\(\widehat{A}=100^{\circ},\widehat{C}=60^{\circ}\)

Bài giải:

a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD

CB = CD (gt) => C thuộc đường trung trực của BD.

Vậy AC là đường trung trực của BD.

b) Xét ABC và ADC có AB = AD (gt)

BC = DC (gt)

AC cạnh chung

nên \(\bigtriangleup ABC = \bigtriangleup ADC\) (c.c.c)

Suy ra: \(\widehat{B}=\widehat{D}\)

Ta có \(\widehat{B}+\widehat{D}=360^{\circ}-100^{\circ}-60^{\circ}=200^{\circ}\)

Do đó \(\widehat{B}+\widehat{D}=100^{\circ}\)