Download.vn Học tập Lớp 7 Toán 7 CTST

Toán 7 Bài 1: Góc và cạnh của một tam giác Giải Toán lớp 7 trang 44 sách Chân trời sáng tạo - Tập 2

Tải về Bình luận
  • 11
Mục lục

Giải Toán lớp 7 Bài 1: Góc và cạnh của một tam giác bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 7 Tập 2 Chân trời sáng tạo trang 44, 45, 46, 47.

Lời giải Toán 7 Bài 1 Chân trời sáng tạo trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 7, từ đó học tốt môn Toán lớp 7 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài 1 Chương 8: Tam giác. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 7 bài 1: Góc và cạnh của một tam giác Chân trời sáng tạo

Giải Toán 7 Chân trời sáng tạo tập 2 Bài 1 - Thực hành

Thực hành 1

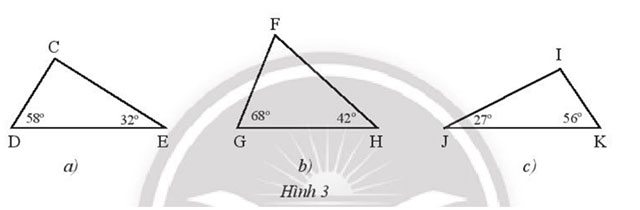
Tìm số đo các góc chưa biết của các tam giác trong Hình 3 và cho biết tam giác nào là tam giác nhọn, tam giác nào là tam giác tù, tam giác nào là tam giác vuông.

Hình 3

Gợi ý đáp án:

a. Xét tam giác CDE có: \hat{C} + \hat{D} + \hat{E} = 180^{\circ}

⇒ \hat{C} = 180^{\circ} - \hat{D} - \hat{E} = 180^{\circ} - 58^{\circ} - 32^{\circ} = 90^{\circ}

Tam giác CDE là tam giác vuông.

b. Xét tam giác GHF có: \hat{F} + \hat{G} + \hat{H} = 180^{\circ}

⇒ \hat{F} = 180^{\circ} - \hat{G} - \hat{H} = 180^{\circ} - 68^{\circ} - 42^{\circ} = 70^{\circ}

Tam giác FGH là tam giác nhọn.

c. Xét tam giác IJK có: \hat{I} + \hat{J} + \hat{K} = 180^{\circ}

⇒ \hat{I} = 180^{\circ} - \hat{J} - \hat{K} = 180^{\circ} - 27^{\circ} - 56^{\circ} = 97^{\circ}

Tam giác IJK là tam giác tù.

Thực hành 2

Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?

a) 7 cm; 8 cm; 11 cm;

b) 7 cm; 9 cm; 16 cm;

c) 8 cm; 9 cm; 16 cm.

Gợi ý đáp án:

a) Ta thấy 11 < 7 + 8 nên bộ ba độ dài 7 cm; 8 cm; 11 cm có thể là độ dài ba cạnh của một tam giác.

b) Ta thấy 16 = 7 + 9 nên bộ ba độ dài 7 cm; 9 cm; 16 cm không thể là độ dài ba cạnh của một tam giác.

c) Ta thấy 16 < 8 + 9 nên bộ ba độ dài 8 cm; 9 cm; 16 cm có thể là độ dài ba cạnh của một tam giác.

Giải Toán 7 Chân trời sáng tạo trang 46, 47 tập 2

Bài 1

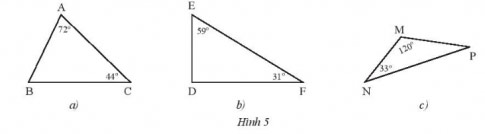
Tìm số đo các góc chưa biết của các tam giác trong Hình 5.

Hình 5

Gợi ý đáp án:

a. \widehat{A} =180^{o}-\widehat{A}-\widehat{C}= 180^{0} - 72^{0} - 44^{0} = 64^{0}

b. \widehat{D} =180^{o}-\widehat{E}-\widehat{F}= 180^{0} - 59^{0} - 31^{0} = 90^{0}

c. \widehat{M} = 180^{o}-\widehat{N}-\widehat{P}= 180^{0} - 120^{0} - 33^{0} = 27^{0}

Bài 2

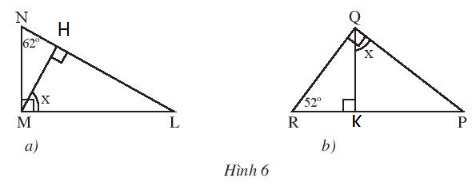
Tìm số đo của góc x trong Hình 6

Hình 6

Gợi ý đáp án:

a) Gọi H là chân vuông góc kẻ từ M xuống cạnh NL.

Xét tam giác NML vuông tại M có: \widehat{L} = 180^{0} - 90^{0} - 62^{0} = 28^{0}.

Xét tam giác MLH vuông tại H có: \widehat{M} + \widehat{L} = 180^{o}-90^{0}=62^{0}.

Vậyx = 62^{0}.

b) Gọi K là chân đường vuông góc kẻ từ Q xuống cạnh RP.

Xét tam giác QRK có \widehat{QHR} = 90^{0}

Nên \widehat{RQK} = 90^{0} - \widehat{R} = 90^{0} - 52^{0} = 38^{0}

Vì \widehat{RQP} = 90^{0}= \widehat{RQK}+\widehat{KQP}

\Rightarrow x = 90^{0} - \widehat{RQK} = 90^{0} - 38^{0} = 52^{0}.

Vậy x = 52^{0}.

Bài 3

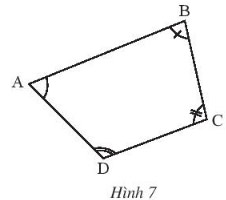
Hãy chia tứ giác ABCD trong hình 7 thành hai tam giác để tính tổng số đo của bốn góc \widehat{A} , \widehat{B}, \widehat{C}, \widehat{D}.

Hình 7

Gợi ý đáp án:

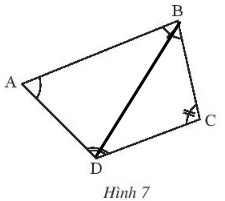
Hình 7

Nối đoạn thẳng BD.

Xét tam giác ABD có: \widehat{A}+\widehat{ABD}+\widehat{ADB}=180^{o}.

Xét tam giác BDC có: \widehat{C}+\widehat{CBD}+\widehat{CDB}=180^{o}.

\Rightarrow \widehat{A} + \widehat{B}+\widehat{C}+\widehat{D} = \widehat{A}+\widehat{ABD}+\widehat{CBD}+\widehat{ADB} + \widehat{CDB} +\widehat{C}

= 180^{o} + 180^{o} = 360^{o}

Vậy \widehat{A} + \widehat{B}+\widehat{C}+\widehat{D} = 360^{o}

Bài 4

Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?

a) 4cm, 5cm, 7cm

b) 2cm, 4cm, 6cm

c) 3cm, 4cm, 8cm

Gợi ý đáp án:

a) 5 - 4 < 7 < 4 + 5.

b) 2+ 4 = 6.

c) 3 + 4 < 8.

Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba câu a) 4cm, 5cm, 7cm có thể là độ dài ba cạnh của một tam giác.

Bài 5

Cho tam giác ABC có BC = 1cm, AB = 4cm. Tìm độ dài cạnh AC (theo đơn vị cm), biết rằng độ dài này là một số nguyên.

Gợi ý đáp án:

Áp dụng đính lí về độ dài 3 cạnh của một tam giác ta có: 4 - 1 < AC < 4 + 1, hay 3 < AC < 5.

Vì độ đài AC là một số nguyên, nên độ dài AC có thể là: 4.

Thử lại giá trị vừa tìm được 5 < 3 + 4 thỏa mãn định lí.

Vậy độ dài AC = 4cm.

Bài 6

Trong một trường học, người ta đánh dấu ba khu vực A, B, C là ba đỉnh của một tam giác, biết khoảng cách AC = 15m, AB = 45m.

a. Nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 30m thì tại khu vực B có nhận được tín hiệu không? Vì sao?

b. Cũng câu hỏi như trên với thiết bị phát wifi có bán kính hoạt động 60m.

Gợi ý đáp án:

Áp dụng định lí về độ dài 3 cạnh của một tam giác có: 45 - 15 < BC < 45 + 15, hay 30 < BC < 60.

a) Nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 30 m thì khu vực B không nhận được tín hiệu vì BC > 30 m.

b) Nếu đặt ở C một thiết bị phát wifi có bán kính hoạt động 60 m thì khu vực B nhận được tín hiệu vì BC < 60 m.

Chia sẻ bởi: 👨 Lê Thị tuyết Mai
Mời bạn đánh giá!
  • Lượt tải: 21
  • Lượt xem: 1.211
  • Dung lượng: 302,2 KB
Liên kết tải về

Link Download chính thức:

Tìm thêm: Chân trời sáng tạo Chân trời sáng tạo Lớp 7
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần

    Toán 7: Chân trời sáng tạo