Toán 7 Bài tập cuối chương 7 - Chân trời sáng tạo Giải Toán lớp 7 trang 42 - Tập 2

Mục lục

Bài sau

Giải Toán lớp 7 Bài tập cuối chương 7 bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 7 Tập 2 Chân trời sáng tạo trang 42.

Lời giải Toán 7 Chân trời sáng tạo trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 7, từ đó học tốt môn Toán lớp 7 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài tập cuối chương 7: Biểu thức đại số. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 7 Bài tập cuối chương 7 Chân trời sáng tạo

Giải Toán 7 Chân trời sáng tạo trang 42 tập 2

Xem thêm

Giải Toán 7 Chân trời sáng tạo trang 42 tập 2

Bài 1

Cho A = x²y + 2xy − 3y²+ 4. Tính giá trị của biểu thức A khi x = -2; y = 3.

Gợi ý đáp án:

Thay x = -2, y = 3 vào biểu thức A ta được:

$A = (-2)^{2} \times 3 + 2 \times (-2) \times 3 - 3 \times 32 + 4$ $A = (- 2)^{2} \times 3 + 2 \times (- 2) \times 3 - 3 \times 32 + 4$

A = 4 x 3 + (-4) x 3 - 3 x 9 + 4

A = 12 - 12 - 27 + 4

A = -23

Vậy A = -23 khi x = -2, y = 3.

Bài 2

Trong các biểu thức sau, biểu thức nào là đơn thức một biến?

a) 2y

b) 3x+5

c) 8

d) 21t¹²

Gợi ý đáp án:

Biểu thức là đơn thức một biến là:

a) 2y

c) 8

d) 21t¹²

Bài 3

Trong các biểu thức sau, biểu thức nào là đa thức một biến?

3 + 6y;

$\frac{2}{x+1}$ $\frac{2}{x + 1}$ ;

7x²+2x−4x⁴+1

$\frac{1}{3}x−5$ $\frac{1}{3} x - 5$

Gợi ý đáp án:

Biểu thức là đa thức một biến:

3 + 6y;

7x²+2x−4x⁴+1

$\frac{1}{3}x−5$ $\frac{1}{3} x - 5$

Bài 4

Hãy viết một đa thức một biến bậc ba có 3 số hạng.

Gợi ý đáp án:

Có nhiều cách để viết một đa thức một biến bậc ba có 3 số hạng.

Chẳng hạn đa thức P(x) là đa thức một biến x bậc ba có 3 số hạng như sau:

$P(x) = x^{3} + 3x^{2} + 1$ $P (x) = x^{3} + 3 x^{2} + 1$ .

Bài 5

Hãy cho biết bậc của các đa thức sau:

A = 3x − 4x² + 1

B = 7

M = x − 7x³ + 10x⁴ + 2

Gợi ý đáp án:

Đa thức A bậc 2.

Đa thức B bậc 0.

Đa thức M bậc 4.

Bài 6

Cho đa thức $P(x) = x^{3}+27$ $P (x) = x^{3} + 27$ . Tìm nghiệm của P(x) trong tập hợp {0; 3; -3}.

Gợi ý đáp án:

Với x = 0, $P(0) = 0^{3}+27 = 27$ $P (0) = 0^{3} + 27 = 27$ .

Với x = -3, $P(-3) = (-3)^{3}+27 = 0$ $P (- 3) = (- 3)^{3} + 27 = 0$ .

Với x = 3, $P(3) = 3^{3}+27 = 54$ $P (3) = 3^{3} + 27 = 54$ .

Vậy x = -3 là nghiệm của đa thức P(x).

Bài 7

Tam giác trong hình 1 có chu vi bằng (25y - 8) cm. Tìm cạnh chưa biết trong tam giác đó.

Bài 7

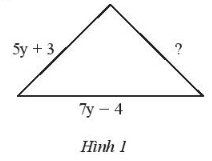
Gợi ý đáp án:

Độ dài cạnh chưa biết trong tam giác là:

(25y - 8) - (5y + 3) - (7y - 4)

= 25y - 8 - 5y - 3 - 7y + 4

= (25y - 5y - 7y) + (-8 - 3 + 4)

= 13y - 7

Vậy độ dài cạnh còn lại trong tam giác đó là 13y - 7 cm.

Bài 8

Cho đa thức: $M(x) = 2x^{4} - 5x^{3} + 7x^{2} + 3x$ $M (x) = 2 x^{4} - 5 x^{3} + 7 x^{2} + 3 x$ .

Tìm các đa thức N(x), Q(x) sao cho: $N(x) - M(x) = -4x^{4} - 2x^{3} + 6x^{2} + 7$ $N (x) - M (x) = - 4 x^{4} - 2 x^{3} + 6 x^{2} + 7$ và $Q(x) + M(x) = 6x^{5} - x^{4} + 3x^{2} - 2$ $Q (x) + M (x) = 6 x^{5} - x^{4} + 3 x^{2} - 2$ .

Gợi ý đáp án:

Do $N(x) - M(x) = -4x^{4} - 2x^{3} + 6x^{2} + 7$ $N (x) - M (x) = - 4 x^{4} - 2 x^{3} + 6 x^{2} + 7$

nên $N(x) = M(x) + (-4x^{4} - 2x^{3} + 6x^{2} + 7)$ $N (x) = M (x) + (- 4 x^{4} - 2 x^{3} + 6 x^{2} + 7)$

N(x) = $2x^{4} - 5x^{3} + 7x^{2} + 3x - 4x^{4} - 2x^{3} + 6x^{2} + 7$ $2 x^{4} - 5 x^{3} + 7 x^{2} + 3 x - 4 x^{4} - 2 x^{3} + 6 x^{2} + 7$

N(x) = $(2x^{4} - 4x^{4}) + (-5x^{3} - 2x^{3}) + (7x^{2} + 6x^{2}) + 3x + 7$ $(2 x^{4} - 4 x^{4}) + (- 5 x^{3} - 2 x^{3}) + (7 x^{2} + 6 x^{2}) + 3 x + 7$

N(x) = $-2x^{4} - 7x^{3} + 13x^{2} + 3x + 7$ $- 2 x^{4} - 7 x^{3} + 13 x^{2} + 3 x + 7$

Do $Q(x) + M(x) = 6x^{5} - x^{4} + 3x^{2} - 2$ $Q (x) + M (x) = 6 x^{5} - x^{4} + 3 x^{2} - 2$ nên Q(x) = $6x^{5} - x^{4} + 3x^{2} - 2 - M(x)$ $6 x^{5} - x^{4} + 3 x^{2} - 2 - M (x)$

Q(x) = $6x^{5} - x^{4} + 3x^{2} - 2 - (2x^{4} - 5x^{3} + 7x^{2} + 3x)$ $6 x^{5} - x^{4} + 3 x^{2} - 2 - (2 x^{4} - 5 x^{3} + 7 x^{2} + 3 x)$

Q(x) = $6x^{5} - x^{4} + 3x^{2} - 2 - 2x^{4} + 5x^{3} - 7x^{2} - 3x$ $6 x^{5} - x^{4} + 3 x^{2} - 2 - 2 x^{4} + 5 x^{3} - 7 x^{2} - 3 x$

Q(x) = $6x^{5} + (-x^{4} - 2x^{4}) + 5x^{3} + (3x^{2} - 7x^{2}) - 3x - 2$ $6 x^{5} + (- x^{4} - 2 x^{4}) + 5 x^{3} + (3 x^{2} - 7 x^{2}) - 3 x - 2$

Q(x) = $6x^{5} - 3x^{4} + 5x^{3} - 4x^{2} - 3x - 2$ $6 x^{5} - 3 x^{4} + 5 x^{3} - 4 x^{2} - 3 x - 2$

Vậy N(x) = $-2x^{4} - 7x^{3} + 13x^{2} + 3x + 7$ $- 2 x^{4} - 7 x^{3} + 13 x^{2} + 3 x + 7$ ; Q(x) = $6x^{5} - 3x^{4} + 5x^{3} - 4x^{2} - 3x - 2$ $6 x^{5} - 3 x^{4} + 5 x^{3} - 4 x^{2} - 3 x - 2$ .

Bài 9

Thực hiện phép nhân

a. (3x - 2)(4x + 5)

b. $(x^{2} - 5x + 4)(6x + 1)$ $(x^{2} - 5 x + 4) (6 x + 1)$

Gợi ý đáp án:

a) $(3 x - 2) (4 x + 5) = 3 x (4 x + 5) - 2 (4 x + 5)$

$=12x^{2}+15x-8x-10=12x^{2}+7x-10$ $= 12 x^{2} + 15 x - 8 x - 10 = 12 x^{2} + 7 x - 10$

b) $(x^{2} - 5x + 4)(6x + 1)=x^{2}(6x + 1)-5x(6x + 1)+4(6x + 1)$ $(x^{2} - 5 x + 4) (6 x + 1) = x^{2} (6 x + 1) - 5 x (6 x + 1) + 4 (6 x + 1)$

$=6x^{3}+x^{2}-30x^{2}-5x+24x+4=6x^{3}-29x^{2}+19x+4$ $= 6 x^{3} + x^{2} - 30 x^{2} - 5 x + 24 x + 4 = 6 x^{3} - 29 x^{2} + 19 x + 4$

Bài 10

Thực hiện phép chia:

a) $(45x^{5}-5x^{4}+10x^{2}):5x^{2}$ $(45 x^{5} - 5 x^{4} + 10 x^{2}) : 5 x^{2}$ ;

b) $(9t^{2}-3t^{4}+27t^{5}):(3t)$ $(9 t^{2} - 3 t^{4} + 27 t^{5}) : (3 t)$ .

Gợi ý đáp án:

a) $(45x^{5}-5x^{4}+10x^{2}):5x^{2}$ $(45 x^{5} - 5 x^{4} + 10 x^{2}) : 5 x^{2}$

$=(45x^{5}:5x^{2})+(-5x^{4}:5x^{2})+(10x^{2}:5x^{2})$ $= (45 x^{5} : 5 x^{2}) + (- 5 x^{4} : 5 x^{2}) + (10 x^{2} : 5 x^{2})$

$=9x^{3}-x^{2}+2$ $= 9 x^{3} - x^{2} + 2$

b) $(9t^{2}-3t^{4}+27t^{5}):(3t)$ $(9 t^{2} - 3 t^{4} + 27 t^{5}) : (3 t)$

$=(9t^{2}:3t)+(-3t^{4}:3t)+(27t^{5}:3t)$ $= (9 t^{2} : 3 t) + (- 3 t^{4} : 3 t) + (27 t^{5} : 3 t)$

$=3t-t^{3}+9t^{4}$ $= 3 t - t^{3} + 9 t^{4}$

Bài 11

Thực hiện phép chia:
a) $(2y^{4}-13y^{3}+15y^{2}+11y-3):(y^{2}-4y-3)$ $(2 y^{4} - 13 y^{3} + 15 y^{2} + 11 y - 3) : (y^{2} - 4 y - 3)$

b) $(5x^{3}-3x^{2}+10):(x^{2}+1)$ $(5 x^{3} - 3 x^{2} + 10) : (x^{2} + 1)$

Lời giải:

a) Thực hiện đặt phép chia ta được:

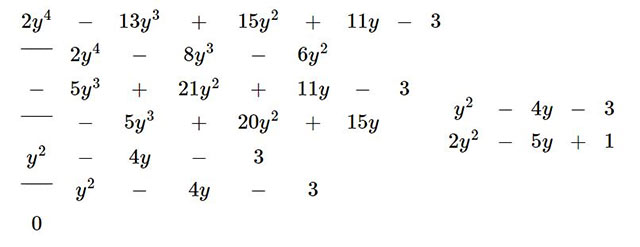
Toán 7

Vậy $(2y^{4} - 13y^{3} + 15y^{2} + 11y - 3) \div (y^{2} - 4y - 3)$ $(2 y^{4} - 13 y^{3} + 15 y^{2} + 11 y - 3) \div (y^{2} - 4 y - 3)$ = $2y^{2} - 5y + 1$ $2 y^{2} - 5 y + 1$ .

b) Thực hiện phép chia ta được:

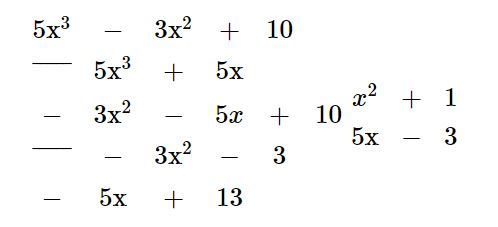
Toán 7

Chia sẻ bởi:

Lê Thị tuyết Mai

Tải về

Bài trước

Bài 5: Hoạt động thực hành và trải nghiệm: Cách tính điểm trung bình môn học kì

Liên kết tải về

Toán 7 Bài tập cuối chương 7 - Chân trời sáng tạo 226,8 KB Tải về

Tìm thêm: Chân trời sáng tạo Chân trời sáng tạo Lớp 7

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!