Toán 7 Bài 2: Tam giác bằng nhau Giải Toán lớp 7 trang 48 sách Chân trời sáng tạo - Tập 2

Giải bài tập SGK Toán 7 Tập 2 trang 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58 sách Chân trời sáng tạo giúp các em học sinh lớp 7 xem gợi ý giải các bài tập của Bài 2: Tam giác bằng nhau.

Thông qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 2 Chương 8 - Tam giác trong sách giáo khoa Toán 7 Tập 2 Chân trời sáng tạo. Đồng thời, cũng giúp thầy cô tham khảo để soạn giáo án cho học sinh của mình theo chương trình mới. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 7 Chân trời sáng tạo trang 57, 58 tập 2

Bài 1

Quan sát Hình 23 rồi thay dấu ? bằng tên tam giác thích hợp.

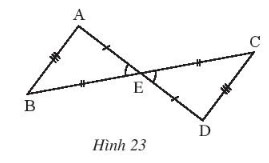
a. \(\Delta ABE = \Delta ?\)

b. \(\Delta EAB = \Delta ?\)

c. \(\Delta ? = \Delta CDE\)

Gợi ý đáp án:

a. \(\Delta ABE = \Delta DCE\)

b. \(\Delta EAB = \Delta EDC\)

c. \(\Delta BAE = \Delta CDE\)

Bài 2

Cho \(\Delta DEF = \Delta HIK\) và \(\widehat{D} = 73^{0}\), DE = 5cm, IK = 7cm. Tính số đo \(\widehat{H}\) và độ dài HI, EF.

Gợi ý đáp án:

Theo đề bài có \(\Delta DEF = \Delta HIK\), nên ta có:

HI = DE = 5cm

EF = IK = 7cm

\(\widehat{H} = \widehat{D} = 73^{0}\)

Bài 3

Cho hai tam giác bằng nhau ABC và DEF (các đỉnh viết chưa tương ứng), trong đó \(\widehat{A} = \widehat{E}, \widehat{C} = \widehat{D}\). Tìm các cặp cạnh bằng nhau, cặp góc tương ứng bằng nhau còn lại.

Gợi ý đáp án:

Xếp theo thứ tự tương ứng các đỉnh có: \(\Delta ABC = \Delta EFD\).

Các cặp góc tương ứng bằng nhau: \(\widehat{ABC} = \widehat{EFD}, \widehat{ACB} = \widehat{EDF}, \widehat{BCA} = \widehat{FDE}\).

Các cặp cạnh bằng nhau là: AB = EF, BC = FD, AC = ED.

Bài 4

Cho biết \(\Delta MNP = \Delta DEF\) và MN = 4cm, MP = 5cm, EF = 6cm. Tính chu vi tam giác MNP

Gợi ý đáp án:

Vì \(\Delta MNP = \Delta DEF\) nên NP = EF = 6cm.

Chu vi tam giác MNP là: MN + MP + NP = 4 + 5 + 6 = 15 (cm)

Bài 5

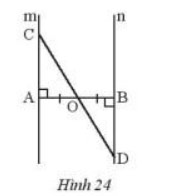
Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB tại A và B. Lấy điểm C trên m, CO cắt n tại D (hình 24). Chứng minh rằng O là trung điểm của CD.

Gợi ý đáp án:

Xét \(\Delta AOC\) vuông tại A và \Delta BOD vuông tại B có:

\(\widehat{COA} = \widehat{DOB}\) (2 góc đối đỉnh).

AO = OB

Suy ra \(\Delta AOC = \Delta BOD\) (cạnh góc vuông và góc nhọn).

\(\Rightarrow OC = OD\)

mà 3 điểm O, C, D thẳng hàng

\(\Rightarrow O\) là trung điểm của CD.

Bài 6

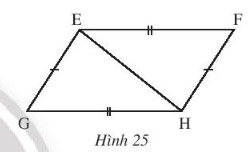
Cho hình 25 có EF = HG, EG = HF.

Chứng minh rằng:

a. \(\Delta EFH = \Delta HGE\)

b. EF // HG

Gợi ý đáp án:

a. Xét \(\Delta EFH\) và \(\Delta HGE\) có:

EH chung

GH = EF

GE = HF

Suy ra \(\Delta EFH = \Delta HGE\) (c.c.c)

b. Theo a: \(\Delta EFH = \Delta HGE\) nên\(\widehat{FEH}= \widehat{EHG}\)

Mà 2 góc này ở vị trí so le trong

Suy ra EF // HG.

Bài 7

Cho tam giác FGH có FG = FH. Lấy điểm I trên cạnh GH sao cho FI là tia phân giác của \(\widehat{GFH}\). Chứng minh rằng hai tam giác FIG và FIH bằng nhau

Gợi ý đáp án:

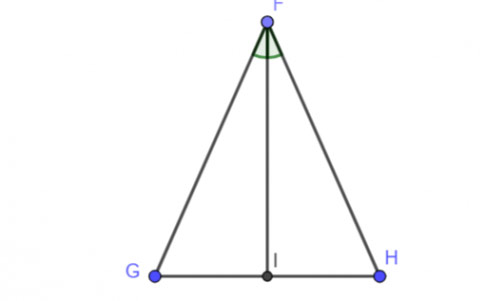
Xét \(\Delta FGI\) và \(\Delta FHI\) có:

FI chung

\(\widehat{GFI}= \widehat{HFI}\)

FG = FH

Suy ra \(\Delta FGI = \Delta FHI\) (c.g.c).

Bài 8

Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm AD và BC. Chứng minh rằng:

a) AD = BC.

b) \(\Delta EAB = \Delta ECD\).

c) OE là tia phân giác của góc xOy.

Gợi ý đáp án:

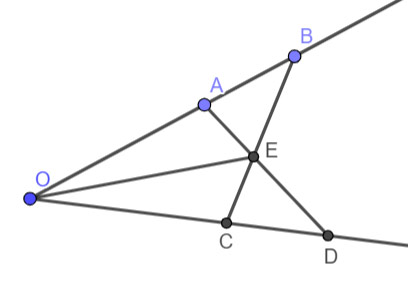
a) Xét\(\Delta AOD\) và \(\Delta COB\) có:

AO = CO

\(\widehat{O}\) chung

OD = OB

Suy ra \(\Delta AOD = \Delta COB\) (c.g.c).

\(\Rightarrow AD = BC\)

b. + \(\Delta ODA = \Delta OBC\) nên \(\widehat{EBA} = \widehat{EDC}\)

Mà \(\widehat{AEB} = \widehat{CED}\)

=> \(\widehat{EAB} = \widehat{ECD}\)

Ta lại có: OA = OC và OB = OD

=> OB - OA = OD - OC

=> AB = CD

+ Xét\(\Delta EAB\) và \(\Delta ECD\) ta có:

\(\widehat{EAB} = \widehat{ECD}\) (chứng minh trên)

AB = CD (chứng minh trên)

\(\widehat{EBA} = \widehat{EDC}\) (chứng minh trên).

Suy ra \(\Delta EAB = \Delta ECD\) (g.c.g)

c. Xét \(\Delta OBE\) và \(\Delta ODE\) có:

OE chung

OB = OD

EB = ED (vì \(\Delta EAB = \Delta ECD\))

Suy ra \(\Delta OBE = \Delta ODE\) nên \(\widehat{BOE} = \widehat{DOE}\).

Suy ra OE là tia phân giác góc xOy.

Bài 9

Đặt tên cho một số điểm có trong Hình 26 và chỉ ra ba cặp tam giác bằng nhau trong hình đó.

Gợi ý đáp án:

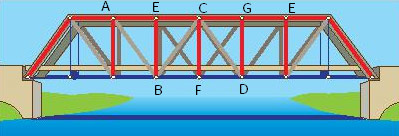
\(\Delta ABC = \Delta EFG = \Delta CDE\)