Toán 10 Bài 3: Tích của một số với một vectơ Giải SGK Toán 10 trang 97 - Tập 1 sách Chân trời sáng tạo

Mục lục

Toán 10 bài 3 Chân trời sáng tạo trang 97 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi phần thực hành và 7 bài tập trong SGK bài Tích của một số với một vectơ .

Giải Toán 10 Chân trời sáng tạo bài 3 trang 97 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán 10 tập 1. Giải Toán 10 bài 3 Chân trời sáng tạo là tài liệu cực kì hữu ích hỗ trợ các em học sinh lớp 10 trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn. Vậy sau đây là nội dung chi tiết giải Toán 10 bài 3 Tích của một số với một vectơ mời các bạn cùng theo dõi.

Toán 10 Bài 3: Tích của một số với một vectơ

Trả lời câu hỏi Thực hành Toán 10 Bài 3
Giải Toán 10 trang 97 Chân trời sáng tạo - Tập 1
Lý thuyết Tích của một số với một vectơ

Trả lời câu hỏi Thực hành Toán 10 Bài 3

Thực hành 1

Cho hai vecto $\overrightarrow a ;\overrightarrow b$ $\vec{a}; \vec{b}$ và một điểm M như Hình 3.

a) Hãy vẽ các vecto $\overrightarrow {MN} = 3\overrightarrow a ;\overrightarrow {MP} = - 3\overrightarrow b$ $\vec{M N} = 3 \vec{a}; \vec{M P} = - 3 \vec{b}$

b) Cho biết mỗi ô vương có cạnh bằng 1. Tính $\left| {3\overrightarrow b } \right|;\left| { - 3\overrightarrow b } \right|;\left| {2\overrightarrow a + 2\overrightarrow b } \right|$ $| 3 \vec{b} |; | - 3 \vec{b} |; | 2 \vec{a} + 2 \vec{b} |$

Gợi ý đáp án

a) Ta có: $\overrightarrow {MN} = 3\overrightarrow a \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\overrightarrow {MN} \nearrow \nearrow \overrightarrow a } \\ {\left| {\overrightarrow {MN} } \right| = 3\left| {\overrightarrow a } \right|} \end{array}} \right.$ $\vec{M N} = 3 \vec{a} \Rightarrow {\begin{matrix} \vec{M N} ↗↗ \vec{a} \\ | \vec{M N} | = 3 | \vec{a} | \end{matrix}$

Từ M vẽ đường thẳng song song với giá của $\overrightarrow a$ $\vec{a}$ , lấy điểm N trên đường thẳng đó cùng hướng với vecto $\overrightarrow a$ $\vec{a}$ thỏa mãn $\left| {\overrightarrow {MN} } \right| = 3\left| {\overrightarrow a } \right|$ $| \vec{M N} | = 3 | \vec{a} |$

Ta lại có: $\overrightarrow {MP} = - 3\overrightarrow b \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\overrightarrow {MP} \nearrow \swarrow \overrightarrow b } \\ {\left| {\overrightarrow {MP} } \right| = 3\left| {\overrightarrow b } \right|} \end{array}} \right.$ $\vec{M P} = - 3 \vec{b} \Rightarrow {\begin{matrix} \vec{M P} ↗↙ \vec{b} \\ | \vec{M P} | = 3 | \vec{b} | \end{matrix}$

Từ M vẽ đường thẳng song song với giá của $\overrightarrow b$ $\vec{b}$ , lấy điểm P trên đường thẳng đó ngược hướng với vecto $\overrightarrow b$ $\vec{b}$ thỏa mãn $\left| {\overrightarrow {MP} } \right| = 3\left| {\overrightarrow b } \right|$ $| \vec{M P} | = 3 | \vec{b} |$

b) Đường chéo mỗi ô vuông có độ dài là $\sqrt 2$ $\sqrt{2}$

Ta có: $\left\{ {\begin{array}{*{20}{c}} {\left| {\overrightarrow a } \right| = 2} \\ {\left| {\overrightarrow b } \right| = 2} \end{array}} \right.$ ${\begin{matrix} | \vec{a} | = 2 \\ | \vec{b} | = 2 \end{matrix}$

Khi đó: $\left\{ {\begin{array}{*{20}{c}} {\left| {3\overrightarrow b } \right| = 3\left| {\overrightarrow b } \right| = 3\sqrt 2 } \\ {\left| { - 3\overrightarrow b } \right| = \left| { - 3} \right|\left| {\overrightarrow b } \right| = 3\sqrt 2 } \end{array}} \right.$ ${\begin{matrix} | 3 \vec{b} | = 3 | \vec{b} | = 3 \sqrt{2} \\ | - 3 \vec{b} | = | - 3 | | \vec{b} | = 3 \sqrt{2} \end{matrix}$

Ta có: $2\overrightarrow a + 2\overrightarrow b = 2\left( {\overrightarrow a + \overrightarrow b } \right)$ $2 \vec{a} + 2 \vec{b} = 2 (\vec{a} + \vec{b})$ (*)

Đặt $\overrightarrow a = \overrightarrow {AC} ;\overrightarrow b = \overrightarrow {AB}$ $\vec{a} = \vec{A C}; \vec{b} = \vec{A B}$ kí hiệu như hình vẽ:

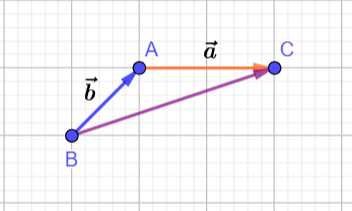
Ta có: $\overrightarrow a + \overrightarrow b = \overrightarrow {AC} + \overrightarrow {AB} = \overrightarrow {BA} + \overrightarrow {AC} = \overrightarrow {BC} \left( {**} \right)$ $\vec{a} + \vec{b} = \vec{A C} + \vec{A B} = \vec{B A} + \vec{A C} = \vec{B C} (* *)$

Từ (*) và (**)

=> $\left| {2\overrightarrow a + 2\overrightarrow b } \right| = \left| {2\left( {\overrightarrow a + \overrightarrow b } \right)} \right| = \left| {2\overrightarrow {BC} } \right| = 2BC$ $| 2 \vec{a} + 2 \vec{b} | = | 2 (\vec{a} + \vec{b}) | = | 2 \vec{B C} | = 2 B C$

Xét tam giác ABC ta có:

$\widehat {BAC} = {45^0} + {90^0} = {135^0}$ $\hat{B A C} = 45^{0} + 90^{0} = 135^{0}$

Áp dụng định lí cosin trong tam giác ta có:

$\begin{matrix} B{C^2} = A{B^2} + A{C^2} - 2AB.AC\cos A \hfill \\ \Rightarrow B{C^2} = {\left( {\sqrt 2 } \right)^2} + {2^2} - 2\left( {\sqrt 2 } \right).2.\cos {135^0} = 10 \hfill \\ \Rightarrow BC = \sqrt {10} \hfill \\ \Rightarrow \left| {2\overrightarrow a + 2\overrightarrow b } \right| = 2BC = 2\sqrt {10} \hfill \\ \end{matrix}$ $\begin{matrix} B C^{2} = A B^{2} + A C^{2} - 2 A B . A C \cos A \\ \Rightarrow B C^{2} = {(\sqrt{2})}^{2} + 2^{2} - 2 (\sqrt{2}) .2 . \cos 135^{0} = 10 \\ \Rightarrow B C = \sqrt{10} \\ \Rightarrow | 2 \vec{a} + 2 \vec{b} | = 2 B C = 2 \sqrt{10} \end{matrix}$

Thực hành 2

Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG}$ $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$

Gợi ý đáp án

Hình vẽ minh họa:

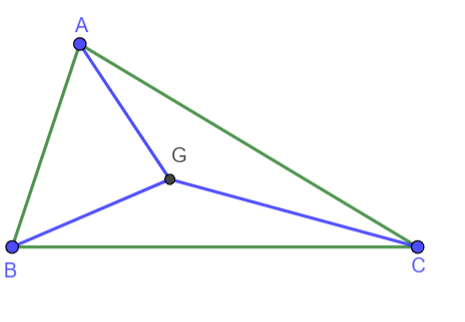
Giả sử G là trọng tâm tam giác ABC

=> $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0$ $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$

Khi đó:

$\begin{matrix} \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \hfill \\ = \left( {\overrightarrow {MG} + \overrightarrow {GA} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GB} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GC} } \right) \hfill \\ = 3\overrightarrow {MG} + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) \hfill \\ = 3\overrightarrow {MG} + \overrightarrow 0 = 3\overrightarrow {MG} \hfill \\ \end{matrix}$ $\begin{matrix} \vec{M A} + \vec{M B} + \vec{M C} \\ = (\vec{M G} + \vec{G A}) + (\vec{M G} + \vec{G B}) + (\vec{M G} + \vec{G C}) \\ = 3 \vec{M G} + (\vec{G A} + \vec{G B} + \vec{G C}) \\ = 3 \vec{M G} + \vec{0} = 3 \vec{M G} \end{matrix}$

Chứng minh chiều ngược lại

Giả sử tam giác ABC có hai điểm M và G bất kì thỏa mãn $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG}$ $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$

Khi đó:

$\begin{matrix} \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} - 3\overrightarrow {MG} = \overrightarrow 0 \hfill \\ \Rightarrow \left( {\overrightarrow {MA} - \overrightarrow {MG} } \right) + \left( {\overrightarrow {MB} - \overrightarrow {MG} } \right) + \left( {\overrightarrow {MC} - \overrightarrow {MG} } \right) = \overrightarrow 0 \hfill \\ \Rightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \hfill \\ \end{matrix}$ $\begin{matrix} \vec{M A} + \vec{M B} + \vec{M C} - 3 \vec{M G} = \vec{0} \\ \Rightarrow (\vec{M A} - \vec{M G}) + (\vec{M B} - \vec{M G}) + (\vec{M C} - \vec{M G}) = \vec{0} \\ \Rightarrow \vec{G A} + \vec{G B} + \vec{G C} = \vec{0} \end{matrix}$

Vậy G là trọng tâm tam giác ABC

Giải Toán 10 trang 97 Chân trời sáng tạo - Tập 1

Bài 1 trang 97

Cho hình bình hành ABCD D có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:

$a) \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO}$ $a) \vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$

$b) \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 2\overrightarrow {AC}$ $b) \vec{A B} + \vec{A C} + \vec{A D} = 2 \vec{A C}$

Gợi ý đáp án

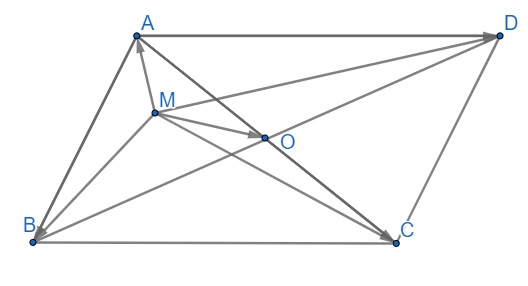
$\Leftrightarrow \overrightarrow {MO} + \overrightarrow {OA} + \overrightarrow {MO} + \overrightarrow {OB} + \overrightarrow {MO} + \overrightarrow {OC} + \overrightarrow {MO} + \overrightarrow {OD} = 4\overrightarrow {MO}$ $\Leftrightarrow \vec{M O} + \vec{O A} + \vec{M O} + \vec{O B} + \vec{M O} + \vec{O C} + \vec{M O} + \vec{O D} = 4 \vec{M O}$

a) $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO}$ $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$

$\Leftrightarrow 4\overrightarrow {MO} + \left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {OC} + \overrightarrow {OD} } \right) = 4\overrightarrow {MO}$ $\Leftrightarrow 4 \vec{M O} + (\vec{O A} + \vec{O B}) + (\vec{O C} + \vec{O D}) = 4 \vec{M O}$

$\Leftrightarrow 4\overrightarrow {MO} + \overrightarrow 0 + \overrightarrow 0 = 4\overrightarrow {MO} \\ \Leftrightarrow 4\overrightarrow {MO} = 4\overrightarrow {MO}$ $\Leftrightarrow 4 \vec{M O} + \vec{0} + \vec{0} = 4 \vec{M O} \Leftrightarrow 4 \vec{M O} = 4 \vec{M O}$ (luôn đúng)

(vì O là giao điểm 2 đường chéo nên là trung điểm của AB, CD)

b) ABCD là hình bình hành nên ta có $\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}$ $\vec{A B} + \vec{A D} = \vec{A C}$

Suy ra $\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \overrightarrow {AC} = \overrightarrow {AC} + \overrightarrow {AC} = 2\overrightarrow {AC}$ $\vec{A B} + \vec{A C} + \vec{A D} = (\vec{A B} + \vec{A D}) + \vec{A C} = \vec{A C} + \vec{A C} = 2 \vec{A C}$ (đpcm)

Bài 2 trang 97

Cho tứ giác ABCD gọi M và N lần lượt là trung điểm của các cạnh AB và CD . Chứng minh rằng

$a) \overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN}$ $a) \vec{A C} + \vec{B D} = 2 \vec{M N}$

$b) \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD}$ $b) \vec{A C} + \vec{B D} = \vec{B C} + \vec{A D}$

Gợi ý đáp án

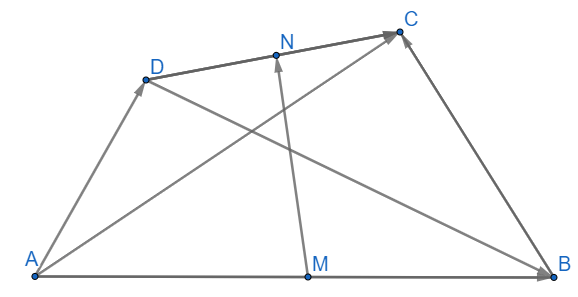
$a) \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} \\= \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right)$ $a) \vec{A C} + \vec{B D} = \vec{A M} + \vec{M N} + \vec{N C} + \vec{B M} + \vec{M N} + \vec{N D} = (\vec{A M} + \vec{B M}) + (\vec{M N} + \vec{M N}) + (\vec{N C} + \vec{N D})$

$= \overrightarrow 0 + 2\overrightarrow {MN} + \overrightarrow 0 = 2\overrightarrow {MN}$ $= \vec{0} + 2 \vec{M N} + \vec{0} = 2 \vec{M N}$ (đpcm)

b) $\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD}$ $\vec{A C} + \vec{B D} = \vec{B C} + \vec{A D}$

$\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND}$ $\vec{B C} + \vec{A D} = \vec{B M} + \vec{M N} + \vec{N C} + \vec{A M} + \vec{M N} + \vec{N D}$

$\left( {\overrightarrow {BM} + \overrightarrow {AM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) = 2\overrightarrow {MN}$ $(\vec{B M} + \vec{A M}) + (\vec{M N} + \vec{M N}) + (\vec{N C} + \vec{N D}) = 2 \vec{M N}$

Mặt khác ta có: $\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN}$ $\vec{A C} + \vec{B D} = 2 \vec{M N}$

Suy ra $\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD}$ $\vec{A C} + \vec{B D} = \vec{B C} + \vec{A D}$

Bài 3 trang 97

Cho hai điểm phân biệt A và B. Xác định điểm M sao cho $\overrightarrow {MA} + 4\overrightarrow {MB} = \overrightarrow 0$ $\vec{M A} + 4 \vec{M B} = \vec{0}$

Gợi ý đáp án

$\overrightarrow {MA} + 4\overrightarrow {MB} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MA} = - 4\overrightarrow {MB} \Rightarrow \frac{{MA}}{{MB}}$ $\vec{M A} + 4 \vec{M B} = \vec{0} \Leftrightarrow \vec{M A} = - 4 \vec{M B} \Rightarrow \frac{M A}{M B}$

$= \frac{{\left| {\overrightarrow {MA} } \right|}}{{\left| {\overrightarrow {MB} } \right|}} = \frac{{\left| { - 4\overrightarrow {MB} } \right|}}{{\left| {\overrightarrow {MB} } \right|}} = 4 và hai vectơ \overrightarrow {MA} ,\overrightarrow {MB}$ $= \frac{| \vec{M A} |}{| \vec{M B} |} = \frac{| - 4 \vec{M B} |}{| \vec{M B} |} = 4 v à h a i v e c t ơ \vec{M A}, \vec{M B}$ ngược hướng

Suy ra M nằm giữa AB sao cho $\frac{{MA}}{{MB}} = 4$ $\frac{M A}{M B} = 4$

Bài 4 trang 97

Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MG}$ $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M G}$

Gợi ý đáp án

$\begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \left( {\overrightarrow {MG} + \overrightarrow {GE} + \overrightarrow {EA} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GE} + \overrightarrow {EB} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GF} + \overrightarrow {FC} } \right)\\ + \left( {\overrightarrow {MG} + \overrightarrow {GF} + \overrightarrow {FD} } \right)\end{array}$ $\begin{array}{l} \vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = (\vec{M G} + \vec{G E} + \vec{E A}) + (\vec{M G} + \vec{G E} + \vec{E B}) + (\vec{M G} + \vec{G F} + \vec{F C}) \\ + (\vec{M G} + \vec{G F} + \vec{F D}) \end{array}$

$= \left( {\overrightarrow {MG} + \overrightarrow {MG} + \overrightarrow {MG} \overrightarrow { + MG} } \right) + 2\left( {\overrightarrow {GE} + \overrightarrow {GF} } \right) + \left( {\overrightarrow {EA} + \overrightarrow {EB} } \right) + \left( {\overrightarrow {FC} + \overrightarrow {FD} } \right)$ $= (\vec{M G} + \vec{M G} + \vec{M G} \vec{+ M G}) + 2 (\vec{G E} + \vec{G F}) + (\vec{E A} + \vec{E B}) + (\vec{F C} + \vec{F D})$

$= 4\overrightarrow {MG} + 2.\overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = 4\overrightarrow {MG}$ $= 4 \vec{M G} + 2. \vec{0} + \vec{0} + \vec{0} = 4 \vec{M G}$ (đpcm)

Bài 5 trang 97

Máy bay A đang bay về hướng Đông Bắc với tốc độ 600 km/h. Cùng lúc đó, máy bay B đang bay về hướng Tây Nam với tốc độ 800 km/h. Biểu diễn vectơ vận tốc \overrightarrow b của máy bay B theo vectơ vận tốc $\overrightarrow a$ $\vec{a}$ của máy bay A

Gợi ý đáp án

vectơ $\overrightarrow a ,\;\overrightarrow b$ $\vec{a}, \vec{b}$ là vectơ vận tốc của máy bay A và máy bay b.

Do đó $\left| {\overrightarrow a } \right|,\;\left| {\overrightarrow b } \right|$ $| \vec{a} |, | \vec{b} |$ lần lượt là độ lớn của vectơ vận tốc tương ứng.

Ta có: $\left| {\overrightarrow a } \right| = 600,\;\left| {\overrightarrow b } \right| = 800$ $| \vec{a} | = 600, | \vec{b} | = 800$

$\Rightarrow \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{800}}{{600}} = \frac{4}{3}$ $\Rightarrow \frac{| \vec{b} |}{| \vec{a} |} = \frac{800}{600} = \frac{4}{3}$

Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó $\overrightarrow b = - \frac{4}{3}\overrightarrow a$ $\vec{b} = - \frac{4}{3} \vec{a}$

Bài 6 trang 97

Cho 2 điểm phân biệt A và B

a) Xác định điểm O sao cho $\overrightarrow {OA} + 3\overrightarrow {OB} = \overrightarrow 0$ $\vec{O A} + 3 \vec{O B} = \vec{0}$

b) Chứng minh rằng với mọi điểm M, ta có $\overrightarrow {MA} + 3\overrightarrow {MB} = 4\overrightarrow {MO}$ $\vec{M A} + 3 \vec{M B} = 4 \vec{M O}$

Gợi ý đáp án

$a) \overrightarrow {OA} + 3\overrightarrow {OB} = \overrightarrow 0$ $a) \vec{O A} + 3 \vec{O B} = \vec{0}$

$\begin{array}{l} \overrightarrow {OA} + 3\overrightarrow {OB} = \vec 0\\ \Leftrightarrow \overrightarrow {OB} + \overrightarrow {BA} + 3\overrightarrow {OB} = \vec 0\\ \Leftrightarrow \overrightarrow {OB} + 3\overrightarrow {OB} = - \overrightarrow {BA} \\ \Leftrightarrow 4\overrightarrow {OB} = \overrightarrow {AB} \\ \Leftrightarrow \overrightarrow {OB} = \frac{1}{4}\overrightarrow {AB} \end{array}$ $\begin{array}{l} \vec{O A} + 3 \vec{O B} = \vec{0} \\ \Leftrightarrow \vec{O B} + \vec{B A} + 3 \vec{O B} = \vec{0} \\ \Leftrightarrow \vec{O B} + 3 \vec{O B} = - \vec{B A} \\ \Leftrightarrow 4 \vec{O B} = \vec{A B} \\ \Leftrightarrow \vec{O B} = \frac{1}{4} \vec{A B} \end{array}$

Vậy O thuộc đoạn AB sao cho $OB = \frac{1}{4}AB$ $O B = \frac{1}{4} A B$

b) Ta có:

$\begin{array}{l} \overrightarrow {MA} + 3\overrightarrow {MB} = \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + 3\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right)\\ = \left( {\overrightarrow {MO} + 3\overrightarrow {MO} } \right) + \left( {\overrightarrow {OA} + 3\overrightarrow {OB} } \right)\\ = 4\overrightarrow {MO} + \overrightarrow 0 = 4\overrightarrow {MO} . (đpcm) \end{array}$ $\begin{array}{l} \vec{M A} + 3 \vec{M B} = (\vec{M O} + \vec{O A}) + 3 (\vec{M O} + \vec{O B}) \\ = (\vec{M O} + 3 \vec{M O}) + (\vec{O A} + 3 \vec{O B}) \\ = 4 \vec{M O} + \vec{0} = 4 \vec{M O} . (đ p c m) \end{array}$

Bài 7 trang 97

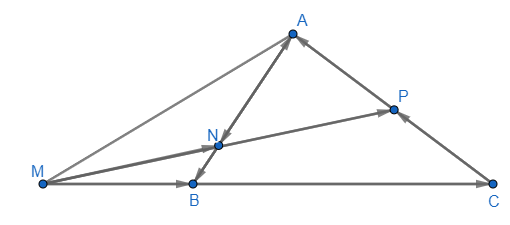
Cho tam giác ABC

a) Xác định các điểm M, N, P thỏa mãn: $\overrightarrow {MB} = \frac{1}{2}\overrightarrow {BC} ,\overrightarrow {AN} = 3\overrightarrow {NB} ,\overrightarrow {CP} = \overrightarrow {PA}$ $\vec{M B} = \frac{1}{2} \vec{B C}, \vec{A N} = 3 \vec{N B}, \vec{C P} = \vec{P A}$

b) Biểu thị mỗi vectơ $\overrightarrow {MN} ,\overrightarrow {MP}$ $\vec{M N}, \vec{M P}$ theo hai vectơ $\overrightarrow {BC} ,\overrightarrow {BA}$ $\vec{B C}, \vec{B A}$

c) Chứng minh ba điểm M, N, P thẳng hàng

Gợi ý đáp án

a) Ta có:

+) $\overrightarrow {MB} = \frac{1}{2}\overrightarrow {BC} \Rightarrow \overrightarrow {MB}$ $\vec{M B} = \frac{1}{2} \vec{B C} \Rightarrow \vec{M B}$ và $\overrightarrow {BC}$ $\vec{B C}$ cùng hướng; tỉ số độ dài $\frac{{BC}}{{MB}} = 2$ $\frac{B C}{M B} = 2$

$\Rightarrow M$ $\Rightarrow M$ nằm ngoài đoạn thẳng BC sao cho $MB = \frac{1}{2}BC$ $M B = \frac{1}{2} B C$

$+) {\overrightarrow {AN} = 3\overrightarrow {NB} \Rightarrow \overrightarrow {AB} + \overrightarrow {BN} = 3\overrightarrow {NB} \Rightarrow 4\overrightarrow {NB} = \overrightarrow {AB} \Leftrightarrow \overrightarrow {NB} = \frac{1}{4}\overrightarrow {AB} }$ $+) \vec{A N} = 3 \vec{N B} \Rightarrow \vec{A B} + \vec{B N} = 3 \vec{N B} \Rightarrow 4 \vec{N B} = \vec{A B} \Leftrightarrow \vec{N B} = \frac{1}{4} \vec{A B}$

$\Rightarrow N$ $\Rightarrow N$ thuộc đoạn thẳng AB và $NB=\frac{{1}}{{4}} AB$ $N B = \frac{1}{4} A B$

$+) \overrightarrow {CP} = \overrightarrow {PA} \Leftrightarrow \overrightarrow {PC} + \overrightarrow {PA} = \overrightarrow 0$ $+) \vec{C P} = \vec{P A} \Leftrightarrow \vec{P C} + \vec{P A} = \vec{0}$

$\Rightarrow P$ $\Rightarrow P$ là trung điểm của CA

$b) \overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BN} = \frac{1}{2}\overrightarrow {BC} + \frac{1}{4}\overrightarrow {BA}$ $b) \vec{M N} = \vec{M B} + \vec{B N} = \frac{1}{2} \vec{B C} + \frac{1}{4} \vec{B A}$

$\begin{array}{l}\overrightarrow {MP} = \overrightarrow {MC} + \overrightarrow {CP} = \overrightarrow {MC} + \frac{1}{2}\overrightarrow {CA} \\= \frac{3}{2}\overrightarrow {BC} + \frac{1}{2}\left( {\overrightarrow {BA} - \overrightarrow {BC} } \right)\\ = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {BA} \end{array}$ $\begin{array}{l} \vec{M P} = \vec{M C} + \vec{C P} = \vec{M C} + \frac{1}{2} \vec{C A} \\ = \frac{3}{2} \vec{B C} + \frac{1}{2} (\vec{B A} - \vec{B C}) \\ = \vec{B C} + \frac{1}{2} \vec{B A} \end{array}$

c) Ta có:

$\overrightarrow {MN} = \frac{1}{2}\overrightarrow {BC} + \frac{1}{4}\overrightarrow {BA} ; \overrightarrow {MP} = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {BA}$ $\vec{M N} = \frac{1}{2} \vec{B C} + \frac{1}{4} \vec{B A}; \vec{M P} = \vec{B C} + \frac{1}{2} \vec{B A}$

$\Rightarrow \overrightarrow {MP} = 2\overrightarrow {MN}$ $\Rightarrow \vec{M P} = 2 \vec{M N}$

Vậy M,N,P thẳng hàng

Lý thuyết Tích của một số với một vectơ

+) Tích của một vectơ $\overrightarrow a \ne \overrightarrow 0$ $\vec{a} \neq \vec{0}$ với một số thực k là một vectơ, kí kiệu là $k\overrightarrow a$ $k \vec{a}$ .

+) vectơ $k\overrightarrow a$ $k \vec{a}$ có độ dài bằng $\left| k \right|\left| {\overrightarrow a } \right|$ $| k | | \vec{a} |$ và

Cùng hướng với vectơ $\overrightarrow a$ $\vec{a}$ nếu k > 0

Ngược hướng với vectơ $\overrightarrow a$ $\vec{a}$ nếu k < 0

+) Quy ước: $k\overrightarrow a = \overrightarrow 0 \Leftrightarrow \left[ \begin{array}{l}\overrightarrow a = \overrightarrow 0 \\k = 0\end{array} \right.$ $k \vec{a} = \vec{0} \Leftrightarrow [\begin{array}{l} \vec{a} = \vec{0} \\ k = 0 \end{array}$

Nhận xét: Hai vectơ $\overrightarrow a$ $\vec{a}$ và $\overrightarrow b$ $\vec{b}$ cùng phương khi và chỉ khi tồn tại k để $\overrightarrow a = k\overrightarrow b .$ $\vec{a} = k \vec{b} .$

Chia sẻ bởi:

Trịnh Thị Thanh

Tải về

Bài trước

Bài 2: Tổng và hiệu của hai vectơ

Bài sau

Bài 4: Tích vô hướng của hai vectơ

Liên kết tải về

Toán 10 Bài 3: Tích của một số với một vectơ 455,9 KB Tải về

Tìm thêm: Chân trời sáng tạo Chân trời sáng tạo Lớp 10

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!