Toán 10 Bài 2: Tập hợp và các phép toán trên tập hợp Giải SGK Toán 10 trang 19 - Tập 1 sách Kết nối tri thức với cuộc sống

Giải Toán lớp 10 trang 19 Kết nối tri thức tập 1 là tài liệu vô cùng hữu ích, giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần mở đầu, Luyện tập vận dụng và 8 bài tập được nhanh chóng và dễ dàng hơn.

Giải Toán 10 Kết nối tri thức trang 19 tập 1 giúp các em nắm rõ kiến thức cơ bản trong bài học đầu tiên của Toán 10, tránh nhầm lẫn khi tiếp cận kiến thức mới. Giải Toán 10 trang 11 Kết nối tri thức hướng dẫn cách giải các bước giải cụ thể để học sinh biết cách trình bày lời giải khoa học, chính xác. Giúp các em học sinh hệ thống lại nội dung, dễ dàng đối chiếu kết quả, từ đó khắc sâu kiến thức. Vậy sau đây là trọn bộ nội dung Giải Toán 10 Bài 2: Tập hợp và các phép toán trên tập hợp, mời các bạn cùng theo dõi và tải tại đây.

Phần Mở đầu Toán 10 Bài 2

Câu lạc bộ lịch sử có 12 thành viên (không có hai bạn nào trùng tên), tổ chức hai chuyên đề trên một phần mềm họp trực tuyến. Tên các thành viên tham gia mỗi chuyên đề được hiển thị trên màn hình (H.1.1).

Gợi ý đáp án

Sau bài học này ta sẽ giải quyết bài toán trên như sau:

Gọi A là tập hợp các bạn tham gia chuyên đề 1, từ màn hình ta có:

A = {Nam; Tú; Khánh; Hương; Bình; Chi; Ngân}.

Gọi B là tập hợp các bạn tham gia chuyên đề 2, từ màn hình ta có:

B = {Hương; Khánh; Hiền; Chi; Bình; Lam; Tú; Hân}.

Khi đó, tập hợp C các bạn tham gia cả hai chuyên đề bao gồm:

C = A ∪ B = {Nam; Tú; Khánh; Hương; Bình; Chi; Ngân; Hiền; Lam; Hân}.

Như vậy có tất cả 10 bạn tham gia cả hai chuyên đề mà câu lạc bộ Lịch sử có tất cả 12 thành viên và không có thành viên nào trùng tên. Do đó có hai thành viên vắng mặt trong cả hai chuyên đề.

Phần Hoạt động Toán 10 Kết nối tri thức

Hoạt động 1

Trong tình huống trên, gọi A là tập hợp những thành viên tham gia chuyên đề 1, B là tập hợp những thành viên tham gia chuyên đề 2.

A = {Nam; Tú; Hương; Bình; Chi; Ngân; Khánh}

B = {Hương; Khánh; Hiền; Chi; Bình; Lam; Tú; Hân}

a) Nam có một phần tử của tập hợp A không? Ngân có là một phần tử của tập hợp B không?

b) Hãy mô tả các tập hợp A và B bằng cách liệt kê các phần tử.

Lời giải chi tiết

a) Nam hiển thị trên màn hình chuyên đề 1 nên Nam là một phần tử của tập hợp A.

Ngân không hiển thị trên màn hình chuyên đề 2 nên Ngân không là phần tử của tập hợp B.

b) Bằng cách liệt kê các phần tử, ta có:

A = {Nam, Tú, Khánh, Hương, Bình, Chi, Ngân}.

B = {Hương, Khánh, Hiền, Chi, Bình, Lam, Tú, Hân}.

Hoạt động 2

Cho tập hợp:

C = {châu Á châu Mĩ, châu Phi, châu Âu, châu Đại Dương, châu Nam Cực}.

a) Hãy chỉ ra tính chất đặc trưng cho các phần tử của tập hợp C.

b) Tập hợp C có bao nhiêu phần tử?

Lời giải chi tiết

a) Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp C.

Tập hợp C là tập hợp các châu lục trên thế giới.

b) Tập hợp C có 6 phần tử.

Phần Luyện tập Toán 10 Kết nối tri thức

Luyện tập 1

Gọi X là tập nghiệm của phương trình:

x² – 24x + 143 = 0

Các mệnh đề sau đúng hay sai?

Lời giải chi tiết

Giải phương trình:

x² – 24x + 143 = 0

=> x = 13 hoặc x = 11

Vậy X = {13; 11}

=> 13 ∈ X là đúng

=> 11 ∉ X là sai

=> n(X) = 2 là đúng

Luyện tập 2

Giả sử C là tập hợp các hình bình hành có hai đường chéo vuông góc. D là tập hợp các hình vuông

Các mệnh đề sau đúng hay sai?

Lời giải chi tiết

Hình bình hành có hai đường chéo vuông góc là hình thoi.

Hình vuông cũng là hình thoi nhưng hình thoi chưa chắc đã hình vuông.

Suy ra D ⊂ C.

=> Mệnh đề a) và c) sai, mệnh đề b) đúng.

Luyện tập 3

Cho hai tập hợp C = {-4; 0; 1; 2}. Các mệnh đề sau đúng hay sai?

Lời giải chi tiết

a) C là tập con của \(\mathbb{Z}\)

Khẳng định đúng vì các phần tử của C đều thuộc \(\mathbb{Z}\).

b) C là tập con của \(\mathbb{N}\)

Ta có: \(- 4 \notin \mathbb{N}\)

=> Khẳng đính sai.

c) C là tập con của \(\mathbb{R}\)

Khẳng định đúng vì các phần tử của C đều thuộc \(\mathbb{R}\).

Phần Bài tập Toán 10 Kết nối tri thức trang 19

Bài 1.8 trang 19

Gọi X là tập hợp các quốc gia tiếp giáp với Việt Nam. Hãy liệt kê các phần tử của tập hợp X và biểu diễn tập X bằng biểu đồ Ven.

Gợi ý đáp án

X = {Lào; Campuchia; Trung quốc; Thái Lan}

Biểu đồ Ven:

Bài 1.9 trang 19

Kí hiệu E là tập hợp các quốc gia tại khu vực Đông Nam Á.

a) Nếu ít nhất hai phần tử thuộc tập hợp E.

b) Nêu ít nhất hai phần tử không thuộc tập hợp E.

c) Liệt kê các phần tử thuộc tập hợp E. Tập hợp E có bao nhiêu phần tử?

Gợi ý đáp án

a) Việt Nam \(\in\) E; Thái Lan \(\in\) E; Lào \(\in\) E.

b) Nhật Bản \(\notin\) E; Hàn Quốc \(\notin\) E.

c) E = {Việt Nam; Lào; Campuchia; Thái Lan; Myanmar; Malaysia; Singapore; Indonesia; Brunei; Philippines; Đông Timor}

Có 11 nước thuộc khu vực Đông Nam Á. Hay tập hợp E có 11 phần tử (n;(E) = 11).

Bài 1.10 trang 19

Hãy viết tập hợp sau bằng cách nêu tính chất đặc trưng cho các phần tử của tập hợp: A = {0; 4; 8; 12; 16}

Gợi ý đáp án

0; 4; 8; 12; 16 là các bội của 4 và nhỏ hơn 17.

\(A = {n \in \mathbb{N}|\;n \in B(4) và n\;\, < 17}\)

Hoặc:

\(A = {n\; = 4.k|\;k \in \mathbb{N} và k \le 4}\)

Bài 1.11 trang 19

Trong các tập hợp sau, tập hợp nào là tập hợp rỗng?

\(A = \left\{ {x \in \mathbb{R}|\;{x^2} - 6 = 0} \right\};\)

\(B = \left\{ {x \in \mathbb{Z}|\;{x^2} - 6 = 0} \right\}\)

Gợi ý đáp án

Ta có: \({x^2} - 6 = 0 \Leftrightarrow x = \pm \sqrt 6 \in \mathbb{R}\)

\(\Rightarrow A = \left\{ { \pm \sqrt 6 } \right\}\)

Nhưng\(\pm \sqrt 6 \notin \mathbb{Z}\) nên không tồn tại \(x \in \mathbb{Z}\) để \({x^2} - 6 = 0\)

Hay \(B = \emptyset .\)

Bài 1.12 trang 19

Cho \(X = \left\{ {\,a\,;b} \right\}\). Các cách viết sau đúng hay sai? Giải thích kết luận đưa ra.

a) \(a \subset X\)

b)\(\left\{ a \right\} \subset X;\)

c) \(\emptyset \in X;\)

Gợi ý đáp án

a) Cách viết: \(a \subset X\) Sai vì a (là một phần tử của A) không phải là một tập hợp.

Hoặc a là một phần tử của A, nên ta phải dùng kí hiệu “ \(\in\)” thay vì “\(\subset\) ”.

Cách viết đúng: \(a \in X\)

b) Cách viết \(\left\{ a \right\} \subset X\) đúng, vì \(\left\{ a \right\}\) là một tập hợp, có duy nhất một phần tử là a và \(a \in X\)

Thế nên tập hợp \(\left\{ a \right\}\) là một tập con của X.

c) Cách viết \(\emptyset \in X\)sai vì:

\(\emptyset\)là một tập hợp (tập hợp rỗng), không phải là một phần tử.

Cách viết đúng: \(\emptyset \subset X\) (Tập hợp rỗng là tập con của mọi tập hợp).

Bài 1.13 trang 19

Cho \(A = \left\{ {2;5} \right\},\;\,B = \left\{ {5;x} \right\},\;\,C = \left\{ {2;y} \right\}\). Tìm x,y để A = B = C.

Gợi ý đáp án

Để A = B

\(\begin{array}{l} \Rightarrow B \subset A\\ \Leftrightarrow \left\{ {5;x} \right\} \subset \left\{ {2;5} \right\}\\ \Leftrightarrow \left\{ \begin{array}{l}x \ne 5\\x \in \left\{ {2;5} \right\}\end{array} \right.\\ \Leftrightarrow x = 2\end{array}\)

Tương tự, ta có:

\(\begin{array}{l}A = C \Rightarrow C \subset A\\ \Leftrightarrow \left\{ {2;y} \right\} \subset \left\{ {2;5} \right\}\\ \Leftrightarrow \left\{ \begin{array}{l}y \ne 2\\y \in \left\{ {2;5} \right\}\end{array} \right.\\ \Leftrightarrow y = 5\end{array}\)

Vậy x = 2;y = 5 thì A = B = C.

Bài 1.14 trang 19

Cho \(\begin{array}{l}A = C \Rightarrow C \subset A\\ \Leftrightarrow \left\{ {2;y} \right\} \subset \left\{ {2;5} \right\}\\ \Leftrightarrow \left\{ \begin{array}{l}y \ne 2\\y \in \left\{ {2;5} \right\}\end{array} \right.\\ \Leftrightarrow y = 5\end{array}\)

a) Liệt kê các phần tử của hai tập hợp A và B.

b) Hãy xác định các tập hợp \(A \cap B,A \cup B và A\,{\rm{\backslash }}\,B\)

Gợi ý đáp án

a) A = { 3;2;1;0; - 1; - 2; - 3;...}

Tập hợp B là tập các nghiệm nguyên của phương trình \(\left( {5x - 3{x^2}} \right)\left( {{x^2} + 2x - 3} \right) = 0\)

Ta có:

\(\begin{array}{l}\left( {5x - 3{x^2}} \right)\left( {{x^2} + 2x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}5x - 3{x^2} = 0\\{x^2} + 2x - 3 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left[ \begin{array}{l}x = 0\\x = \frac{5}{3}\end{array} \right.\\\left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\end{array} \right.\end{array}\)

Vậy \(B = \left\{ { - 3;0;1} \right\}.\)

\(b) A \cap B = \left\{ {x \in A|x \in B} \right\} = \{ - 3;0;1\} = B\)

\(A \cup B = {x \in A hoặc x \in B} = \{ 3;2;1;0; - 1; - 2; - 3;...\} = A\)

\(A\,{\rm{\backslash }}\,B = \left\{ {x \in A|x \notin B} \right\} = \{ 3;2;1;0; - 1; - 2; - 3;...\} {\rm{\backslash }}\;\{ - 3;0;1\} = \{ 3;2; - 1; - 2; - 4; - 5; - 6;...\}\)

Bài 1.15 trang 19

Xác định các tập hợp sau và biểu diễn chúng trên trục số.

a) \(( - 4;1] \cap [0;3)\)

b) \((0;2] \cup [ - 3;1)\)

\(c) ( - 2;1) \cap ( - \infty ;1]\)

\(d) \mathbb{R}{\rm{\backslash }}( - \infty ;3]\)

Gợi ý đáp án

a) Ta có:

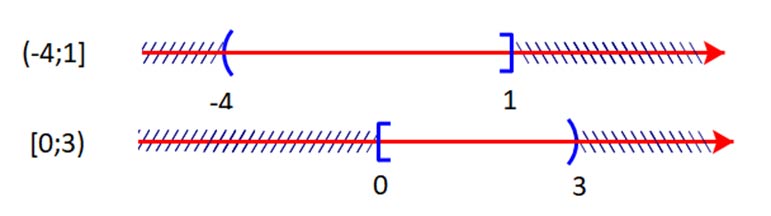
Giao của hai tập hợp là \(( - 4;1] \cap [0;3) = \left[ {0;1} \right]\)

b) Ta có:

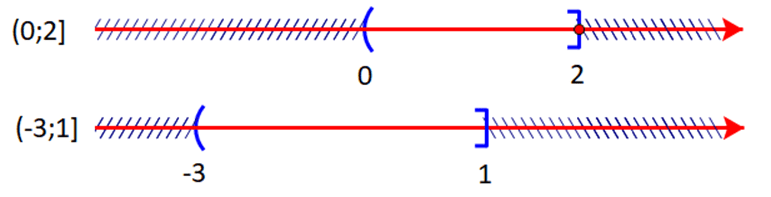
Hợp của hai tập hợp là \((0;2] \cup ( - 3;1] = ( - 3;2]\)

c) Ta có:

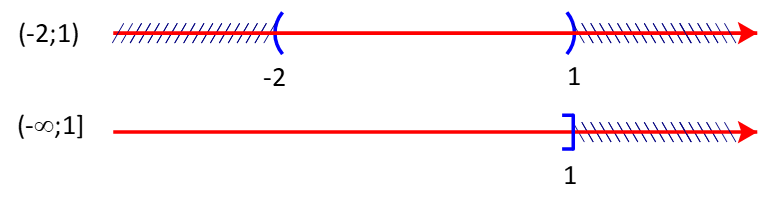
Giao của hai tập hợp là \(( - 2;1) \cap ( - \infty ;1] = ( - 2;1)\)

d) Ta có:

Phần bù của tập hợp\(( - \infty ;3] trong \mathbb{R} là \mathbb{R}{\rm{\backslash }}( - \infty ;3] = (3; + \infty )\)

Bài 1.16 trang 19

Để phục vụ cho một hội nghị quốc tế, ban tổ chức huy động 35 người phiên dịch tiếng Anh, 30 người phiên dịch tiếng Pháp, trong đó có 16 người phiên dịch được cả hai thứ tiếng Anh và Pháp. Hãy trả lời các câu hỏi sau:

a) Ban tổ chức đã huy động bao nhiêu người phiên dịch cho hội nghị đó?

b) Có bao nhiêu người chỉ phiên dịch được tiếng Anh?

c) Có bao nhiêu người chỉ phiên dịch được tiếng Pháp?

Gợi ý đáp án 

Gọi A là tập hợp những người phiên dịch tiếng Anh, B là tập hợp những người phiên dịch tiếng Pháp.

Ta có:\(n\left( A \right) = 35, n\left( B \right) = 30.\)

Biểu đồ Ven

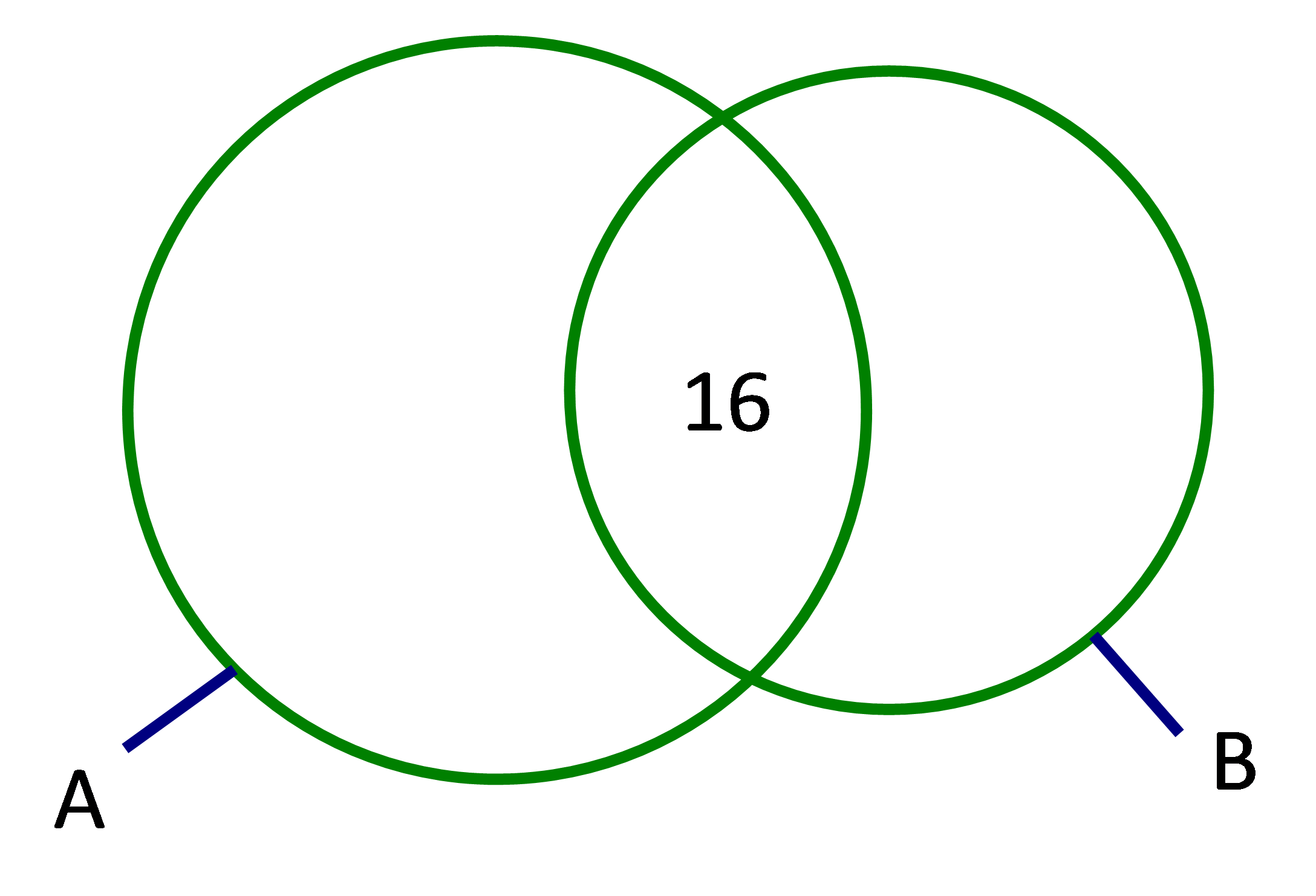
\(a) n\;\left( {A \cup B} \right) = n\;(A) + n\;(B) - n\;(A \cap B) = 35 + 30 - 16 = 49\)

Vậy ban tổ chức đã huy động 49 người phiên dịch cho hội nghị đó

\(b) n\;\left( {A\,{\rm{\backslash }}\,B} \right) = n\;(A) - n\;(A \cap B) = 35 - 16 = 19\)

Vậy có 19 người chỉ phiên dịch được tiếng Anh

\(c) n\left( {B\,{\rm{\backslash }}\,{\rm{A}}} \right) = n\;(B) - n\;(B \cap A) = 30 - 16 = 14\)

Vậy có 14 người chỉ phiên dịch được tiếng Pháp