Toán 10 Bài 2: Định lí Côsin và định lí Sin Giải SGK Toán 10 trang 72 - Tập 1 sách Chân trời sáng tạo

Giải bài 2 trang 72 SGK Toán 10 Chân trời sáng tạo giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi phần vận dụng và bài tập trong SGK bài Định lí Côsin và định lí Sin.

Toán 10 Chân trời sáng tạo trang 72 - Tập 1 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa. Giải Toán 10 Chân trời sáng tạo trang 72 là tài liệu cực kì hữu ích hỗ trợ các em học sinh lớp 10 trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.

Toán 10 Bài 2: Định lí Côsin và định lí Sin

Trả lời Toán lớp 10 Bài 2 phần Vận dụng
Giải Toán 10 trang 72, 73 Chân trời sáng tạo - Tập 1

Trả lời Toán lớp 10 Bài 2 phần Vận dụng

Vận dụng 1

Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 800 m và 900 m người quan sát nhìn hai điểm này dưới một góc 70° (Hình 5).

Lời giải chi tiết

Gọi A là điểm người đứng quan sát, B và C lần lượt là hai đầu của hồ nước.

Khi đó AB = 800 m; AC = 900 m; $\widehat A = {70^0}$

Tính khoảng cách giữa hai đầu hồ nước chính là tính độ dài cạnh BC của tam giác ABC.

Áp dụng định lý côsin cho tam giác ABC ta có:

BC² = AB² + AC²– 2AB.AC.cosA = 800² + 900²– 2.800.900. cos70° ≈ 957 491

Suy ra BC ≈ 978,5 (m).

Vậy khoảng cách giữa hai đầu hồ nước khoảng 978,5 m.

Vận dụng 2

Trong một khu bảo tồn, người ta xây dựng một tháp canh và hai bồn chứa nước A, B để phòng hỏa hoạn. Từ tháp canh, người ta phát hiện đám cháy và số liệu đưa về như Hình 9. Nên dẫn nước từ bồn chứa A hay B để dập tắt đám cháy nhanh hơn?

Lợi ý đáp án

Xét tam giác ADC có:

$\widehat {CAD} + \widehat {ADC} + \widehat {ACD} = {180^0}$

=> $\widehat {ACD} = {180^0} - \left( {\widehat {CAD} + \widehat {ADC}} \right) = {180^0} - \left( {35 + 125} \right) = {20^0}$

Áp dụng định lí cosin cho tam giác ABC ta có:

BC² = AB² + AC² – 2AB.AC.cos34⁰

=> BC ≈ 1206m

=> DC > BC

Vậy để dập tắt đám cháy nhanh hơn thì nước phải lấy từ bồn B.

Giải Toán 10 trang 72, 73 Chân trời sáng tạo - Tập 1

Bài 1 trang 72

Tính độ dài cạnh x trong các tam giác sau:

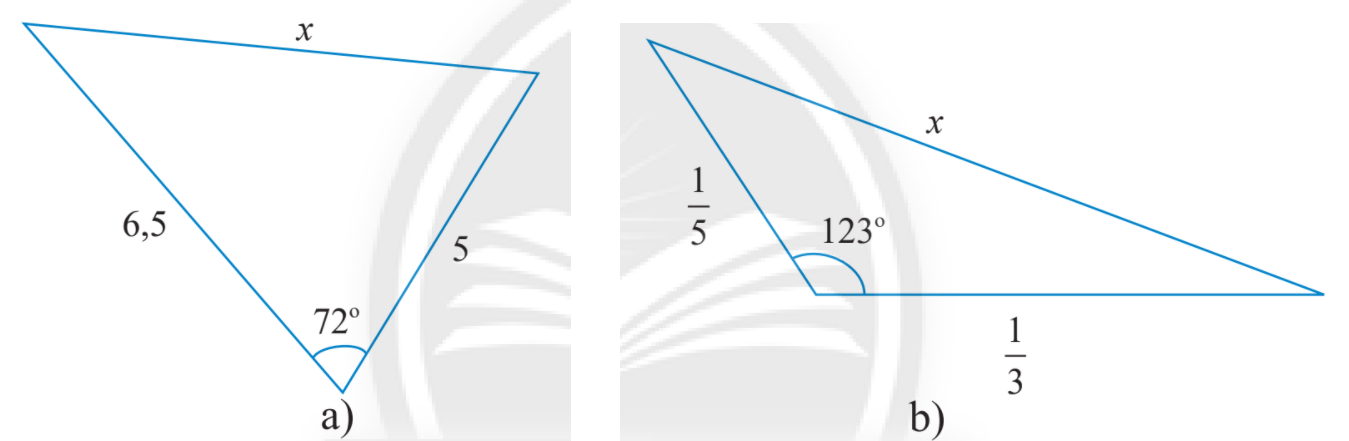
Gợi ý đáp án

a) Áp dụng định lí cosin, ta có:

$\begin{array}{l}{x^2} = 6,{5^2} + {5^2} - 2.6,5.5.\cos {72^o} \approx 47,16\\ \Leftrightarrow x \approx 6,87\end{array}$

b) Áp dụng định lí cosin, ta có:

$\begin{array}{l}{x^2} = {\left( {\frac{1}{5}} \right)^2} + {\left( {\frac{1}{3}} \right)^2} - 2.\frac{1}{5}.\frac{1}{3}.\cos {123^o} \approx 0,224\\ \Leftrightarrow x \approx 0,473\end{array}$

Bài 2 trang 72

Tính độ dài cạnh c trong tam giác ABC ở Hình 14.

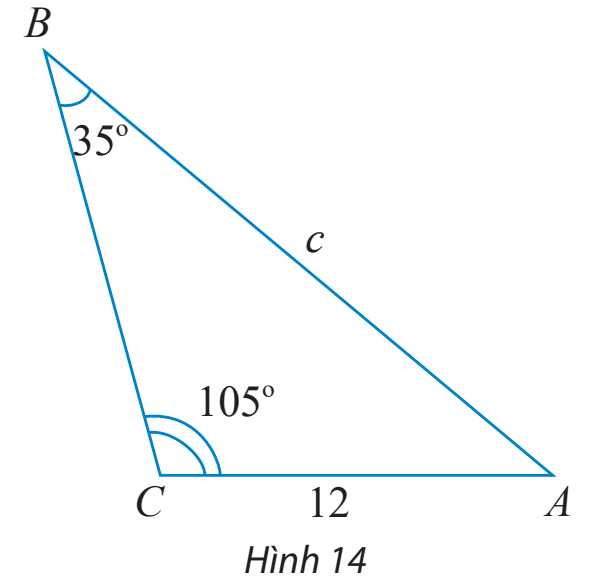
$\frac{c}{{\sin {{105}^o}}} = \frac{{12}}{{\sin {{35}^o}}}$

Gợi ý đáp án

Áp dụng định lí sin, ta có:

$\frac{c}{{\sin {{105}^o}}} = \frac{{12}}{{\sin {{35}^o}}} \Rightarrow c = \frac{{12.\sin {{105}^o}}}{{\sin {{35}^o}}} \approx 20,2$

Bài 3 trang 72

Cho tam giác ABC, biết cạnh $a = 152,\;\widehat B = {79^o},\;\widehat C = {61^o}$ . Tính các góc, các cạnh còn lại và bán kính đường tròn ngoại tiếp của tam giác đó.

Gợi ý đáp án

Đặt AB = c,AC = b,BC = a.

Ta có: $a = 152;\widehat A = {180^o} - ({79^o} + {61^o}) = {40^o}$

Áp dụng định lí sin, ta có:

$\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R$

Suy ra:

$\begin{array}{l}AC = b = \frac{{a.\sin B}}{{\sin A}} = \frac{{152.\sin {{79}^o}}}{{\sin {{40}^o}}} \approx 232,13\\AB = c = \frac{{a.\sin C}}{{\sin A}} = \frac{{152.\sin {{61}^o}}}{{\sin {{40}^o}}} \approx 206,82\\R = \frac{a}{{\sin A}} = \frac{{152}}{{\sin {{40}^o}}} \approx 236,47\end{array}$

Bài 4 trang 73

Một công viên có dạng hình tam giác với các kích thước như Hình 15. Tính số đo các góc của tam giác đó.

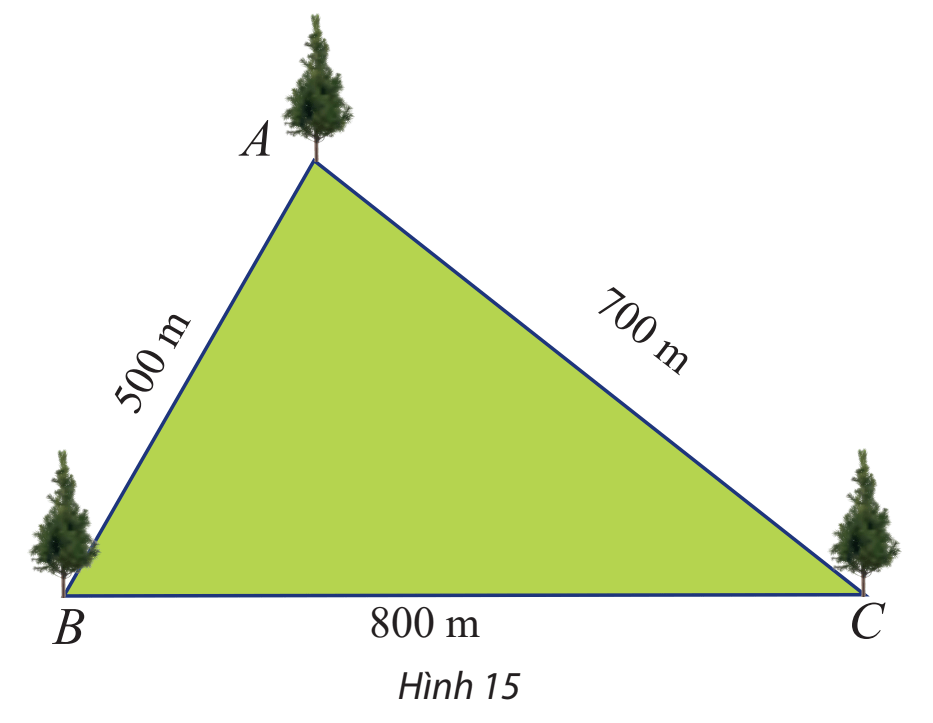
Gợi ý đáp án

Đặt a = BC,b = AC,c = AB

Ta có: a = 800,b = 700,c = 500.

Áp dụng định lí cosin, ta có:

$\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}.$

Suy ra:

$\begin{array}{l}\cos A = \frac{{{{700}^2} + {{500}^2} - {{800}^2}}}{{2.700.500}} = \frac{1}{7} \Rightarrow \widehat A = {81^o}47'12,44'';\\\cos B = \frac{{{{500}^2} + {{800}^2} - {{700}^2}}}{{2.500.800}} = \frac{1}{2} \Rightarrow \widehat B = {60^o};\\\cos C = \frac{{{{800}^2} + {{700}^2} - {{500}^2}}}{{2.800.700}} = \frac{{11}}{{14}} \Rightarrow \widehat C = {38^o}12'47,56''.\end{array}$

Vậy $\widehat A = {81^o}47'12,44'';\widehat B = {60^o};\widehat C = {38^o}12'47,56''.$

Bài 5 trang 73

Tính diện tích một lá cờ hình tam giác cân có độ dài cạnh bên là 90 cm và góc ở đỉnh là ${35^o}.$

Gợi ý đáp án

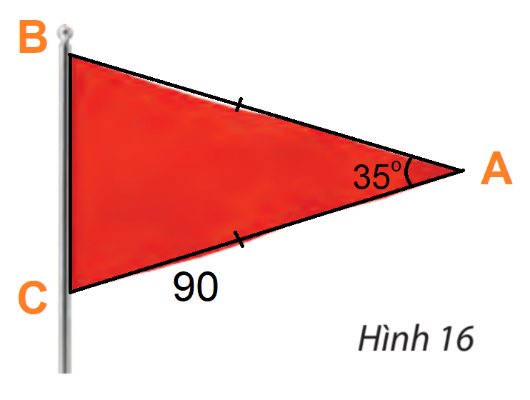
Kí hiệu các điểm A, B, C như hình trên.

Từ giả thiết ta có: $AB = AC = 90,\widehat A = {35^o}$

Áp dụng công thức $S = \frac{1}{2}bc\sin A$ , ta có: $S = \frac{1}{2}.90.90.c\sin {35^o} \approx 2323\;(c{m^2})$

Bài 6 trang 73

Cho tam giác ABC có AB = 6,AC = 8 và $\widehat A = {60^o}.$

a) Tính diện tích tam giác ABC.

b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC.

Gợi ý đáp án

Đặt a = BC,b = AC,c = AB.

a) Áp dụng công thức $S = \frac{1}{2}bc\sin A, ta có: {S_{ABC}} = \frac{1}{2}.8.6.\sin {60^o} = \frac{1}{2}.8.6.\frac{{\sqrt 3 }}{2} = 12\sqrt 3$

b) Áp dụng định lí cosin cho tam giác ABC ta được:

$\begin{array}{l}B{C^2} = {a^2} = {8^2} + {6^2} - 2.8.6.\cos {60^o} = 52\\ \Rightarrow BC = 2\sqrt {13} \end{array}$

Xét tam giác IBC ta có:

Góc $\widehat {BIC} = 2.\widehat {BAC} = {120^o}$ (góc ở tâm và góc nội tiếp cùng chắn một cung)

$IB = IC = R = \frac{a}{{\sin A}} = \frac{{2\sqrt {13} }}{{\frac{{\sqrt 3 }}{2}}} = \frac{{4\sqrt {39} }}{3}.$

$\Rightarrow {S_{IBC}} = \frac{1}{2}.\frac{{4\sqrt {39} }}{3}.\frac{{4\sqrt {39} }}{3}\sin {120^o} = \frac{{52\sqrt 3 }}{3}.$

Bài 7 trang 73

Cho tam giác ABC có trọng tâm G và độ dài ba cạnh AB, BC, CA lần lượt là 15, 18, 27.

a) Tính diện tích và bán kính đường tròn nội tiếp tam giác ABC.

b) Tính diện tích tam giác GBC.

Gợi ý đáp án

a) Đặt a = BC,b = AC,c = AB.

Ta có: $p = \frac{1}{2}(15 + 18 + 27) = 30$

Áp dụng công thức heron, ta có:

${S_{ABC}} = \sqrt {30(30 - 15)(30 - 18)(30 - 27)} = 90\sqrt 2$

Và $r = \frac{S}{p} = \frac{{90\sqrt 2 }}{{30}} = 3\sqrt 2$

b) Gọi, H, K lần lượt là chân đường cao hạ từ A và G xuống BC, M là trung điểm BC.

G là trọng tâm tam giác ABC nên $GM = \frac{1}{3}AM$

$\begin{array}{l} \Rightarrow GK = \frac{1}{3}.AH\\ \Rightarrow {S_{GBC}} = \frac{1}{3}.\,{S_{ABC}} = \frac{1}{3}.90\sqrt 2 = 30\sqrt 2 .\end{array}$

Xét tam giác IBC ta có:

Góc $\widehat {BIC} = 2.\widehat {BAC} = {120^o}$ (góc ở tâm và góc nội tiếp cùng chắn một cung)

$IB = IC = R = \frac{a}{{\sin A}} = \frac{{2\sqrt {13} }}{{\frac{{\sqrt 3 }}{2}}} = \frac{{4\sqrt {39} }}{3}.$

$\Rightarrow {S_{IBC}} = \frac{1}{2}.\frac{{4\sqrt {39} }}{3}.\frac{{4\sqrt {39} }}{3}\sin {120^o} = \frac{{52\sqrt 3 }}{3}.$

Bài 8 trang 73

Cho ${h_a}$ là đường cao vẽ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác ABC. Chứng minh hệ thức: ${h_a} = 2R\sin B\sin C.$

Gợi ý đáp án

Đặt a = BC,b = AC,c = AB

Ta có: $\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b} \Rightarrow {h_a} = b.\sin C$

Theo định lí sin, ta có: $\frac{b}{{\sin B}} = 2R \Rightarrow b = 2R.\sin B$

$\Rightarrow {h_a} = 2R.\sin B.\sin C$

Bài 9 trang 73

Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.

a) Chứng minh \ $frac{{{S_{BDE}}}}{{{S_{BAC}}}} = \frac{{BD.BE}}{{BA.BC}}.$

b) Biết rằng ${S_{ABC}} = 9{S_{BDE}} và DE = 2\sqrt 2$ . Tính $\cos B$ và bán kính đường tròn ngoại tiếp tam giác ABC.

Gợi ý đáp án

a) Áp dụng công thức $S = \frac{1}{2}ac.\sin B$ cho tam giác ABC và BED, ta có:

${S_{ABC}} = \frac{1}{2}.BA.BC.\sin B;{S_{BED}} = \frac{1}{2}..BE.BD.\sin B$

$\Rightarrow \frac{{{S_{BED}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}.BE.BD.\sin B}}{{\frac{1}{2}.BA.BC.\sin B}} = \frac{{BE.BD}}{{BA.BC}}$

b) Ta có: $\cos B = \frac{{BD}}{{BA}} = \frac{{BE}}{{BC}}$

Mà $\frac{{{S_{BED}}}}{{{S_{ABC}}}} = \frac{1}{9} \Rightarrow \frac{{BD}}{{BA}}.\frac{{BE}}{{BC}} = \frac{1}{9}$

$\Rightarrow \cos B = \frac{{BD}}{{BA}} = \frac{{BE}}{{BC}} = \frac{1}{3}$

+) Xét tam giác ABC và tam giác DEB ta có:

$\frac{{BE}}{{BC}} = \frac{{BD}}{{BA}} = \frac{1}{3}$ và góc B chung

$\Rightarrow \Delta ABC \sim \Delta DEB (cgc)$

$\Rightarrow \frac{{DE}}{{AC}} = \frac{1}{3} \Rightarrow AC = 3.DE = 3.2\sqrt 2 = 6\sqrt 2 .$

Ta có: $\cos B = \frac{1}{3} \Rightarrow \sin B = \sqrt {1 - {{\left( {\frac{1}{3}} \right)}^2}} = \frac{{2\sqrt 2 }}{3}$ (do B là góc nhọn)

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{{AC}}{{\sin B}} = 2R \Rightarrow R = \frac{{6\sqrt 2 }}{{\frac{{2\sqrt 2 }}{3}}}:2 = \frac{9}{2}$

Bài 10 trang 73

Cho tứ giác lồi ABCD có các đường chéo AC = x,BD = y và góc giữa AC và BD bằng $\alpha .$ Gọi S là diện tích của tứ giác ABCD.

a) Chứng minh $S = \frac{1}{2}xy.\sin \alpha$

b) Nêu kết quả trong trường hợp $AC \bot BD.$

Gợi ý đáp án

Gọi O là giao điểm của AC và BD.

a) Áp dụng công thức $S = \frac{1}{2}ac.\sin B$ , ta có:

$\begin{array}{l}{S_{OAD}} = \frac{1}{2}.OA.OD.\sin \alpha ;\quad {S_{OBC}} = \frac{1}{2}..OB.OC.\sin \alpha ;\\{S_{OAB}} = \frac{1}{2}.OA.OB.\sin ({180^o} - \alpha );\quad {S_{OCD}} = \frac{1}{2}.OD.OC.\sin ({180^o} - \alpha ).\end{array}$

Mà $\sin ({180^o} - \alpha ) = \sin \alpha$

$\Rightarrow {S_{OAB}} = \frac{1}{2}.OA.OB.\sin \alpha ;\quad {S_{OCD}} = \frac{1}{2}.OD.OC.\sin \alpha .$

$\begin{array}{l} \Rightarrow {S_{ABCD}} = \left( {{S_{OAD}} + {S_{OAB}}} \right) + \left( {{S_{OBC}} + {S_{OCD}}} \right)\\ = \frac{1}{2}.OA.\sin \alpha .(OD + OB) + \frac{1}{2}.OC.\sin \alpha .(OB + OD)\\ = \frac{1}{2}.OA.\sin \alpha .BD + \frac{1}{2}.OC.\sin \alpha .BD\\ = \frac{1}{2}.BD.\sin \alpha .(OA + OC)\\ = \frac{1}{2}.AC.BD.\sin \alpha = \frac{1}{2}.x.y.\sin \alpha .\end{array}$

b) Nếu $AC \bot BD thì \alpha = {90^o} \Rightarrow \sin \alpha = 1.$

$\Rightarrow {S_{ABCD}} = \frac{1}{2}.x.y.1 = \frac{1}{2}.x.y.$

Chia sẻ bởi:

Trịnh Thị Thanh

Download

Mời bạn đánh giá!

Lượt tải: 19
Lượt xem: 16.036
Dung lượng: 644,6 KB

Liên kết tải về

Link Download chính thức:

Toán 10 Bài 2: Định lí Côsin và định lí Sin Download

Tìm thêm: Chân trời sáng tạo Chân trời sáng tạo Lớp 10

1 Bình luận

Sắp xếp theo

Xóa Đăng nhập để Gửi

Nguyễn Anh Nhi
Bài 2 kết quả sai hay sao í
Thích Phản hồi 0 09:31 08/10
- Trịnh Thị Thanh
  bài 2 kết quả bằng 20.2 đúng rồi mà Bạn. Bạn xem lại nhé
  Thích Phản hồi 0 08:30 09/10

Tài liệu tham khảo khác

Chủ đề liên quan

Mới nhất trong tuần

Toán 10 Bài 3: Đường tròn trong mặt phẳng tọa độ
Giải SGK Toán 10 trang 62 - Tập 2 sách Chân trời sáng tạo
Toán 10 Bài 2: Hoán vị, chỉnh hợp và tổ hợp
Giải SGK Toán 10 trang 32 - Tập 2 sách Chân trời sáng tạo
Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân
Giải SGK Toán 10 trang 24 - Tập 2 sách Chân trời sáng tạo
Toán 10 Bài 2: Đường thẳng trong mặt phẳng tọa độ
Giải SGK Toán 10 trang 57 - Tập 2 sách Chân trời sáng tạo
Toán 10 Bài 3: Phương trình quy về bậc hai
Giải SGK Toán 10 trang 17 - Tập 2 sách Chân trời sáng tạo
Toán 10 Bài 1: Tọa độ của vectơ
Giải SGK Toán 10 trang 44 - Tập 2 sách Chân trời sáng tạo
Toán 10 Bài 2: Giải bất phương trình bậc hai một ẩn
Giải SGK Toán 10 trang 12 - Tập 2 sách Chân trời sáng tạo
Toán 10 Bài tập cuối chương III - Chân trời sáng tạo
Giải SGK Toán 10 trang 59 - Tập 1
Toán 10 Bài 1: Số gần đúng và sai số
Giải SGK Toán 10 trang 109 - Tập 1 sách Chân trời sáng tạo
Toán 10 Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ
Giải SGK Toán 10 trang 111 - Tập 1 sách Chân trời sáng tạo

Toán 10 - Chân trời sáng tạo

Toán 10 Bài 2: Định lí Côsin và định lí Sin Giải SGK Toán 10 trang 72 - Tập 1 sách Chân trời sáng tạo