Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn (không bao gồm tài liệu cao cấp) và trải nghiệm website không quảng cáo
Tìm hiểu thêm »Toán 10 Chân trời sáng tạo trang 25 là tài liệu vô cùng hữu ích, giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần mở đầu, thực hành và 6 bài tập được nhanh chóng và dễ dàng hơn.
Giải Toán 10 Chân trời sáng tạo trang 25 giúp các em nắm rõ kiến thức cơ bản trong bài Các phép toán trên tập hợp, tránh nhầm lẫn khi tiếp cận kiến thức mới. Toán 10 Chân trời sáng tạo tập 1 trang 25 hướng dẫn cách giải các bước giải cụ thể để học sinh biết cách trình bày lời giải khoa học, chính xác. Giúp các em học sinh hệ thống lại nội dung, dễ dàng đối chiếu kết quả, từ đó khắc sâu kiến thức. Vậy sau đây là trọn bộ nội dung Giải Toán 10 Bài 3: Các phép toán trên tập hợp mời các bạn cùng theo dõi và tải tại đây.
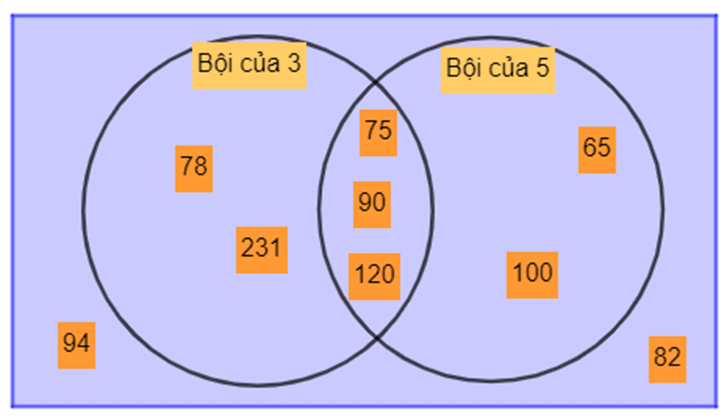
Có hai đường tròn chia một hình chữ nhật thành các miền như hình bên. Hãy đặt mỗi thẻ số sau đây vào miền thích hợp trên hình chữ nhật và giải thích cách làm.
Lời giải:
Trong các số đã cho, ta có:
Các số là bội của 3 là: 75; 78; 90; 120; 231.
Các số là bội của 5 là: 65; 75; 90; 100; 120.
Các số không là bội của 3 cũng không là bội của 5 là: 82 và 94.
Khi đó ta điền được vào miền tương ứng như sau:
Xác định tập hợp A ∪ B và A ∩ B, biết:
a) A = {a; b; c; d; e}, B = {a; e; i; u}
b) A = {x ∈ ℝ| x2+ 2x – 3 = 0}, B = {x ∈ ℝ | |x| = 1}
Gợi ý đáp án
a) Ta có A ∪ B = {a; b; c; d; e; i; u}.
Ta lại có A ∩ B = {a; e}.
Vậy A ∪ B = {a; b; c; d; e; i; u} và A ∩ B = {a; e}.
b) Xét phương trình x2+ 2x – 3 = 0 => x = 1 hoặc x = -1
=> A = {-3; 1}
Xét phương trình |x| = 1
=> B = {-1; 1}.
Vậy A ∪ B = {-3; -1; 1} và A ∩ B = {1}.
Cho A = {(x; y)| x, y ∈ ℝ, 3x – y = 9}, B = {(x; y)| x, y ∈ ℝ, x – y = 1}
Hãy xác định A ⋂ B
Gợi ý đáp án
Ta có: A ∩ B = {(x; y)| x, y ∈ ℝ, x – y = 1 và 3x – y = 9}.
Hay tập hợp A ∩ B gồm các cặp (x; y) với x, y ∈ ℝ thỏa mãn hệ phương trình ![]() \(\left\{ {\begin{array}{*{20}{c}}
{x - y = 1} \\
{3x - y = 9}
\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}
{x - y = 1} \\
{3x - y = 9}
\end{array}} \right.\)
Giải hệ phương trình ![]() \(\left\{ {\begin{array}{*{20}{c}}
{x - y = 1} \\
{3x - y = 9}
\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}
{x - y = 1} \\
{3x - y = 9}
\end{array}} \right.\)
=> A ∩ B = {4; 3}
Vậy A ∩ B = {4; 3}
Cho các tập hợp U = {x ∈ ℕ | x < 8}, A = {0; 1; 2; 3; 4}, B = {3; 4; 5}.
Xác định các tập hợp sau đây:
a) A\B, B\A và (A\B) ∩ (B\A);
b) CE(A ∩ B) và (CEA) ∪ (CEB);
c) CE(A ∪ B) và (CEA) ∩ (CEB).
Gợi ý đáp án
a) Ta có
A\B = {0; 1; 2} và B\A = {5}
=> (A\B) ∩ (B\A) = ∅
b) Ta có: E = {0; 1; 2; 3; 4; 5; 6; 7}
Ta lại có: A ∩ B = {3; 4}
=> CE(A ∩ B) = {0; 1; 2; 5; 6; 7}
Ta có: CEA = {5; 6; 7} và CEB = {0; 1; 2; 6; 7}
=> (CEA) ∪ (CEB) = {0; 1; 2; 5; 6; 7
c) Ta lại có: A ∪ B = {0; 1; 2; 3; 4; 5}
=> CE(A∪ B) = {6; 7}
Ta có: CEA = {5; 6; 7} và CEB = {0; 1; 2; 6; 7}
=> (CEA) ∩ (CEB) = {6; 7}
Xác định các tập hợp sau đây:
|
a) (1; 3) ∪ [- 2; 2] |
b) (-∞; 1) ⋂ [0; π] |
|
c) |
d) |
Gợi ý đáp án
a) (1; 3) ∪ [- 2; 2] = [- 2; 3)
b) (-∞; 1) ⋂ [0; π] = [0; 1)
c) ![]() \(\left[ {\frac{1}{2};3} \right)\backslash \left( {1; + \infty } \right) = \left[ {\frac{1}{2};1} \right]\)
\(\left[ {\frac{1}{2};3} \right)\backslash \left( {1; + \infty } \right) = \left[ {\frac{1}{2};1} \right]\)
d) ![]() \({C_\mathbb{R}}\left[ { - 1; + \infty } \right) = \left( { - \infty ; - 1} \right)\)
\({C_\mathbb{R}}\left[ { - 1; + \infty } \right) = \left( { - \infty ; - 1} \right)\)
Xác định các tập hợp A ![]() \(\cup\) B và A
\(\cup\) B và A ![]() \(\cap\) B với
\(\cap\) B với
a) A = {đỏ; cam; vàng; lục; lam}, B = {lục; làm; chàm; tím}.
b) A là tập hợp các tam giác đều, B là tập hợp các tam giác cân.
Gợi ý đáp án
a) A = {đỏ; cam; vàng; lục; lam}, B = {lục; lam; chàm; tím}.
![]() \(A \cup B = {đỏ; cam; vàng; lục; lam; chàm; tím}\)
\(A \cup B = {đỏ; cam; vàng; lục; lam; chàm; tím}\)
![]() \(A \cap B\) = {lục; lam}
\(A \cap B\) = {lục; lam}
b) Vì mỗi tam giác đều cũng là một tam giác cân nên ![]() \(A \subset B.\)
\(A \subset B.\)
![]() \(A \cup B = B,\;A \cap B = A.\)
\(A \cup B = B,\;A \cap B = A.\)
Xác định các tập hợp A \cap B trong mỗi trường hợp sau:
a![]() \() A = \{ x \in \mathbb{R}|{x^2} - 2 = 0\} ,B = \{ x \in \mathbb{R}|2x - 1 < 0\}\)
\() A = \{ x \in \mathbb{R}|{x^2} - 2 = 0\} ,B = \{ x \in \mathbb{R}|2x - 1 < 0\}\)
b) ![]() \(A = \{ (x;y)|\;x,y \in \mathbb{R},y = 2x - 1\} ,B = \{ (x;y)|\;x,y \in \mathbb{R},y = - x + 5\}\)
\(A = \{ (x;y)|\;x,y \in \mathbb{R},y = 2x - 1\} ,B = \{ (x;y)|\;x,y \in \mathbb{R},y = - x + 5\}\)
c) A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật.
Gợi ý đáp án
a) Phương trình ![]() \({x^2} - 2 = 0\) có hai nghiệm là
\({x^2} - 2 = 0\) có hai nghiệm là ![]() \(\sqrt 2\)và
\(\sqrt 2\)và ![]() \(- \sqrt 2\), nên
\(- \sqrt 2\), nên ![]() \(A = \{ \sqrt 2 ; - \sqrt 2 \}\)
\(A = \{ \sqrt 2 ; - \sqrt 2 \}\)
Tập hợp ![]() \(B = \{ x \in \mathbb{R}|2x - 1 < 0\}\)là tập hợp các số thực
\(B = \{ x \in \mathbb{R}|2x - 1 < 0\}\)là tập hợp các số thực ![]() \(x < \frac{1}{2}\)
\(x < \frac{1}{2}\)
Từ đó ![]() \(A \cap B = \{ - \sqrt 2 \} .\)
\(A \cap B = \{ - \sqrt 2 \} .\)
b) ![]() \(A \cap B = \{ (x;y)|\;x,y \in \mathbb{R},y = 2x - 1,y = - x + 5\}\)
\(A \cap B = \{ (x;y)|\;x,y \in \mathbb{R},y = 2x - 1,y = - x + 5\}\)
Tức là ![]() \(A \cap B\) là tập hợp các cặp số (x; y) thỏa mãn hệ phương trình:
\(A \cap B\) là tập hợp các cặp số (x; y) thỏa mãn hệ phương trình: ![]() \(\left\{ \begin{array}{l}y = 2x - 1\\y = - x + 5\end{array} \right.\)
\(\left\{ \begin{array}{l}y = 2x - 1\\y = - x + 5\end{array} \right.\)
![]() \(\Leftrightarrow \left\{ \begin{array}{l}2x - 1 = - x + 5\\y = 2x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 6\\y = 2x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}2x - 1 = - x + 5\\y = 2x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 6\\y = 2x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\)
Vậy ![]() \(A \cap B = \{ (2;3)\} .\)
\(A \cap B = \{ (2;3)\} .\)
c) A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật.
![]() \(A \cap B\) là tập hợp các hình vừa là hình chữ nhật vừa là hình thoi.
\(A \cap B\) là tập hợp các hình vừa là hình chữ nhật vừa là hình thoi.
Một tứ giác bất kì thuộc ![]() \(A \cap B\) thì nó là hình chữ nhật và có 2 cạnh kề bằng nhau (hình vuông)
\(A \cap B\) thì nó là hình chữ nhật và có 2 cạnh kề bằng nhau (hình vuông)
Do đó ![]() \(A \cap B\) là tập hợp các hình vuông.
\(A \cap B\) là tập hợp các hình vuông.
Cho ![]() \(E = \{ x \in \mathbb{N}|x < 10\} ,A = \{ x \in E|xlà bội của 3\} ,B = \{ x \in E|x\) là ước của 6\} .
\(E = \{ x \in \mathbb{N}|x < 10\} ,A = \{ x \in E|xlà bội của 3\} ,B = \{ x \in E|x\) là ước của 6\} .
Xác định các tập hợp ![]() \(A\backslash B,{\rm{ }}B\backslash A,\;{C_E}A,\;{C_E}B,{C_E}(A \cup B),{C_E}(A \cap B).\)
\(A\backslash B,{\rm{ }}B\backslash A,\;{C_E}A,\;{C_E}B,{C_E}(A \cup B),{C_E}(A \cap B).\)
Gợi ý đáp án
![]() \(E = \{ x \in \mathbb{N}|x < 10\} = \{ 0;1;2;3;4;5;6;7;8;9\}\)
\(E = \{ x \in \mathbb{N}|x < 10\} = \{ 0;1;2;3;4;5;6;7;8;9\}\)
![]() \(A = \{ x \in E|xlà bội của 3\} = \{ 0;3;6;9\}\)
\(A = \{ x \in E|xlà bội của 3\} = \{ 0;3;6;9\}\)
![]() \(B = \{ x \in E|x là ước của 6\} = \{ 0;6\} \Rightarrow B \subset A\)
\(B = \{ x \in E|x là ước của 6\} = \{ 0;6\} \Rightarrow B \subset A\)
Ta có: ![]() \(A\backslash B = \left\{ {3;9} \right\}, B\backslash A = \emptyset\)
\(A\backslash B = \left\{ {3;9} \right\}, B\backslash A = \emptyset\)
![]() \({C_E}A = \{ 1;2;4;5;7;8\} ,\;{C_E}B = \{ 0;1;2;5;6;7\}\)
\({C_E}A = \{ 1;2;4;5;7;8\} ,\;{C_E}B = \{ 0;1;2;5;6;7\}\)
![]() \(A \cap B = B \Rightarrow {C_E}(A \cap B) = {C_E}B = \{ 0;1;2;5;6;7\}\)
\(A \cap B = B \Rightarrow {C_E}(A \cap B) = {C_E}B = \{ 0;1;2;5;6;7\}\)
![]() \(A \cup B = A \Rightarrow {C_E}(A \cup B) = {C_E}A = \{ 1;2;4;5;7;8\}\)
\(A \cup B = A \Rightarrow {C_E}(A \cup B) = {C_E}A = \{ 1;2;4;5;7;8\}\)
Cho A và B là hai tập hợp bất kì. Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Hãy giải thích bằng cách sử dụng biểu đồ Ven.
a) A và A ![]() \(\cup\) B
\(\cup\) B
b) A và A![]() \(\cap\)B
\(\cap\)B
Gợi ý đáp án
Ta có sơ đồ ven sau:
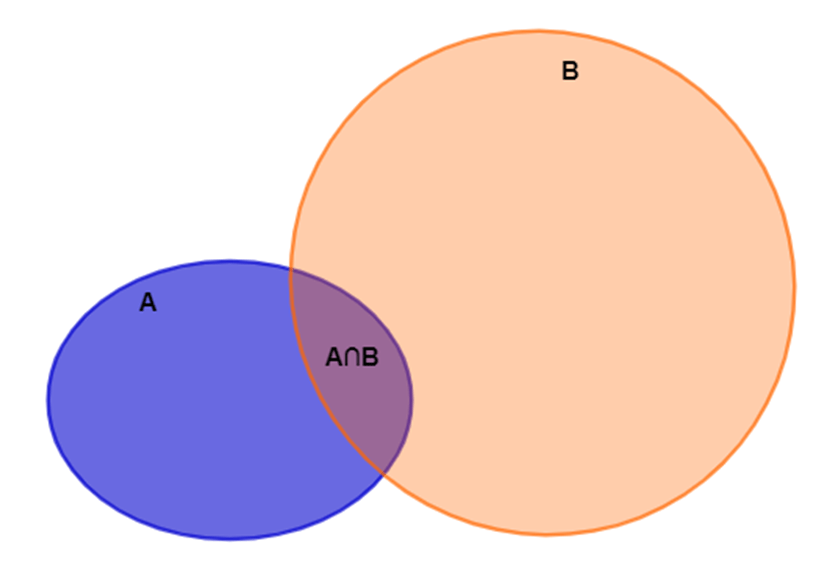
Ta thấy tập hợp A ∪ B bao gồm phần màu xanh, phần màu tím và phần màu cam.
Tập hợp A chứa phần màu xanh cộng màu tím nằm hoàn toàn trong tập hợp A ∪ B. Do đó tập A là tập con của tập A ∪ B. Ta viết A ⊂ (A∪B).
Tập hợp A∩B là phần màu tím và nằm hoàn toàn trong tập hợp A nên tập A∩B là tập con của tập A. Ta viết (A∩B) ⊂ A.
Trong số 35 học sinh của lớp 10H, có 20 học sinh thích học môn Toán, 16 học sinh thích môn Tiếng Anh và 12 học sinh thích cả hai môn này. Hỏi lớp 10H:
a) có bao nhiêu học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh?
b) có bao nhiêu học sinh không thích cả hai môn này?
Gợi ý đáp án
Ta có sơ đồ ven:
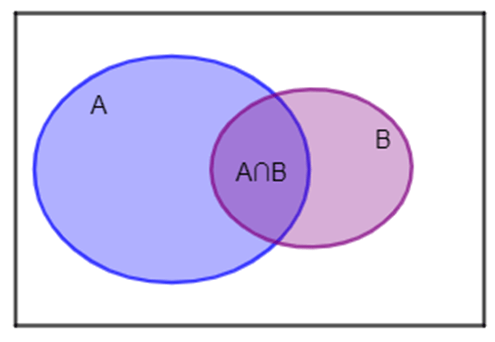
a) Gọi A là tập hợp học sinh của lớp 10H thích học môn Toán, B là tập hợp học sinh của lớp 10H thích học môn Tiếng Anh.
Theo giả thiết, n(A) = 20, n(B) = 16, n(A∩B) = 12.
Nhận thấy rằng, nếu tính tổng n(A) + n(B) thì ta được số học sinh lớp 10H thích môn Toán hoặc Tiếng Anh, nhưng số bạn thích cả hai môn được tính hai lần. Do đó, số bạn học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh là:
n(A∪B) = n(A) + n(B) – n(A∩B) = 20 + 16 – 12 = 24.
Vậy lớp 10H có 24 học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh.
b) Số học sinh của lớp 10H không thích cả hai môn Toán và Tiếng Anh là:
35 – 24 = 11 (học sinh).
Vậy có 11 học sinh của lớp 10H không thích cả hai môn Toán và Tiếng Anh.
Xác định các tập hợp sau đây:
![]() \(a) ( - \infty ;0) \cup [ - \pi ;\pi ]\)
\(a) ( - \infty ;0) \cup [ - \pi ;\pi ]\)
![]() \(b) [ - 3,5;2] \cap ( - 2;3,5)\)
\(b) [ - 3,5;2] \cap ( - 2;3,5)\)
![]() \(c) ( - \infty ;\sqrt 2 ] \cap [1; + \infty )\)
\(c) ( - \infty ;\sqrt 2 ] \cap [1; + \infty )\)
![]() \(d) ( - \infty ;\sqrt 2 ]{\rm{\backslash }}[1; + \infty )\)
\(d) ( - \infty ;\sqrt 2 ]{\rm{\backslash }}[1; + \infty )\)
Gợi ý đáp án
a) Ta có:![]() \((−∞;0]={x∈R|x≤0}−∞;0=x∈ℝ|x≤0\) và
\((−∞;0]={x∈R|x≤0}−∞;0=x∈ℝ|x≤0\) và
![]() \([−π;π]={x∈R|−π≤x≤π}−π;π=x∈ℝ|−π≤x≤π\)
\([−π;π]={x∈R|−π≤x≤π}−π;π=x∈ℝ|−π≤x≤π\)
![]() \(⇒(−∞;0]∪[−π;π]={x∈R|x≤0,−π≤x≤π}={x∈R|−π≤x≤0}\)
\(⇒(−∞;0]∪[−π;π]={x∈R|x≤0,−π≤x≤π}={x∈R|−π≤x≤0}\)
![]() \(=[−π;0].⇒−∞;0∪−π;π=x∈ℝ|x≤0,−π≤x≤π=x∈ℝ|−π≤x≤0=−π;0.\)
\(=[−π;0].⇒−∞;0∪−π;π=x∈ℝ|x≤0,−π≤x≤π=x∈ℝ|−π≤x≤0=−π;0.\)
⇒(−∞;0]∪[−π;π]⇒−∞;0∪−π;π = {x ∈ ℝ | x ≤ 0 hoặc −π≤x≤π
= {x∈R|x≤π} =(−∞;π]−π≤x≤π = x∈ℝ|x≤π =−∞;π }
Vậy ![]() \((−∞;0]∪[−π;π]=(−∞;π]−∞;0∪−π;π=−∞;π.\)
\((−∞;0]∪[−π;π]=(−∞;π]−∞;0∪−π;π=−∞;π.\)
b) Ta có:![]() \([-3,5; 2] = {x∈R|−3,5≤x≤2}x∈ℝ|−3,5≤x≤2\)
\([-3,5; 2] = {x∈R|−3,5≤x≤2}x∈ℝ|−3,5≤x≤2\)
và (-2; 3,5) = {x∈R|−2<x<3,5}x∈ℝ|−2<x<3,5
⇒ [-3,5; 2] ∩ (-2; 3,5) = {x∈R|−2<x≤2}=(−2;2]x∈ℝ|−2<x≤2=−2;2
Vậy ![]() \([-3,5; 2] ∩ (-2; 3,5) = (-2; 2].\)
\([-3,5; 2] ∩ (-2; 3,5) = (-2; 2].\)
c) Ta có ![]() \((−∞;√2]={x∈R∣∣x≤√2}.−∞;2=x∈ℝ|x≤2.\)
\((−∞;√2]={x∈R∣∣x≤√2}.−∞;2=x∈ℝ|x≤2.\)
và ![]() \([1;+∞)={x∈R|x≥1}1;+∞=x∈ℝ|x≥1\)
\([1;+∞)={x∈R|x≥1}1;+∞=x∈ℝ|x≥1\)
![]() \(⇒(−∞;√2]∩[1;+∞)={x∈R∣∣1≤x≤√2}=[1;√2].\)
\(⇒(−∞;√2]∩[1;+∞)={x∈R∣∣1≤x≤√2}=[1;√2].\)
![]() \(⇒−∞;2∩1;+∞=x∈ℝ|1≤x≤2=1;2.\)
\(⇒−∞;2∩1;+∞=x∈ℝ|1≤x≤2=1;2.\)
Vậy ![]() \((−∞;√2]∩[1;+∞)=[1;√2].−∞;2∩1;+∞=1;2.\)
\((−∞;√2]∩[1;+∞)=[1;√2].−∞;2∩1;+∞=1;2.\)
d) Ta có ![]() \((−∞;√2]={x∈R∣∣x≤√2}−∞;2=x∈ℝ|x≤2\) và
\((−∞;√2]={x∈R∣∣x≤√2}−∞;2=x∈ℝ|x≤2\) và
![]() \([1;+∞)={x∈R|x≥1}1;+∞=x∈ℝ|x≥1\)
\([1;+∞)={x∈R|x≥1}1;+∞=x∈ℝ|x≥1\)
![]() \(⇒(−∞;√2][1;+∞) = x∈R∣∣x≤√2\)
\(⇒(−∞;√2][1;+∞) = x∈R∣∣x≤√2\)
⇒−∞;2\1;+∞ = x∈ℝ|x≤2 và x < 1} = (−∞;1)−∞;1
Vậy ![]() \((−∞;√2],1;+∞)=(−∞;1)\)
\((−∞;√2],1;+∞)=(−∞;1)\)
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: