Toán 6 Bài 1: Số nguyên âm và tập hợp các số nguyên Giải Toán lớp 6 trang 53, 54 - Tập 1 sách Chân trời sáng tạo
Giải Toán lớp 6 Bài 1: Số nguyên âm và tập hợp các số nguyên bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 6 Tập 1 Chân trời sáng tạo trang 49, 50, 51, 52, 53, 54.
Lời giải Toán 6 Bài 1 Chân trời sáng tạo trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 6, từ đó học tốt môn Toán lớp 6 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài 1 Chương 2: Số nguyên. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Giải Toán 6 bài 1: Số nguyên âm và tập hợp các số nguyên Chân trời sáng tạo
Giải Toán 6 Chân trời sáng tạo phần Hoạt động
Hoạt động 1
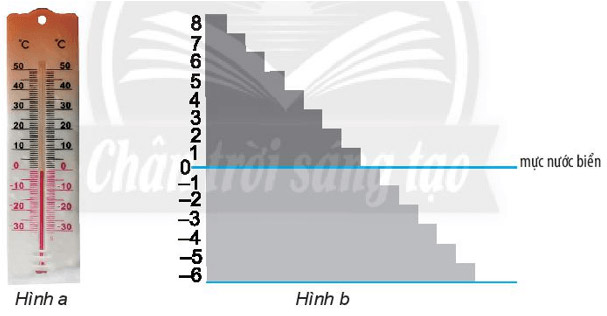
a) Quan sát nhiệt kế trong hình a.
- Hãy đọc các chỉ số nhiệt độ (độ C) ở trên mực số 0.
- Hãy cho biết các số chỉ nhiệt độ ở dưới mực số 0 mang dấu gì.
b) Quan sát hình b, em thấy các bậc thang có độ cao mang dấu trừ thì nằm ở trên hay dưới mực nước biển?
c) Hãy cho biết những phép tính nào dưới đây không thực hiện được trên tập số tự nhiên.
4 + 3; 4 – 3;
2 + 5; 2 – 5;
Gợi ý đáp án:
a) Quan sát nhiệt kế ở hình a, ta nhận thấy các chỉ số nhiệt độ ở trên mức số 0 là: 10 độ C, 20 độ C, 30 độ C, 40 độ C, 50 độ C.
- Các chỉ số nhiệt độ ở dưới mức số 0 mang dấu trừ.
b) Quan sát thang đo ở hình b, ta thấy các bậc thang ở độ cao mang dấu trừ thì nằm bên dưới mực nước biển.
c) Trên tập số tự nhiên, ta thực hiện được các phép tính:
4 + 3 = 7;
2 + 5 = 7;
4 – 3 = 1;
Riêng phép tính 2 – 5 là không thực hiện được trên tập số tự nhiên vì 2 < 5 nên 2 không trừ được cho 5.
Hoạt động 2
Ta đã biết N = {0; 1; 2; 3; 4; …} là tập hợp số tự nhiên.
Còn Z = {…; -3; -2; -1; 0; 1; 2; 3; …} là tập hợp bao gồm các loại số nào?
Gợi ý đáp án:
Tập hợp gồm các số nguyên âm và các số tự nhiên.
Hoạt động 3
Em hãy vẽ vào vở theo hướng dẫn sau:
- Vẽ một đường thẳng nằm ngang, trên đó đánh dấu các điểm cách đều nhau như trong hình.
- Chọn một điểm để ghi số 0 và gọi đó là điểm 0, các điểm bên phải điểm 0 biểu diễn các số nguyên dương và được ghi là 1; 2; 3; … Các điểm bên trái điểm 0 biểu diễn các số nguyên âm và được ghi là -1; -2; -3; …
Chẳng hạn để ghi số 3, ta di chuyển ba vạch về bên phải số 0; để ghi số - 4, ta di chuyển bốn vạch về bên trái số 0.
![]()
Gợi ý đáp án:
Bước 1. Vẽ đường thẳng nằm ngang có mũi tên như sau:
![]()
Bước 2. Trên đường thẳng đánh dấu các điểm cách đều nhau
![]()
Bước 3. Chọn một điểm ở giữa biểu diễn cho số 0.
Bước 4. Về bên phải số 0 biểu diễn các số tăng dần từ trái sang phải lần lượt là 1; 2; 3; …
- Biểu diễn số 1: Ta di chuyển 1 vạch về bên phải số 0.
- Biểu diễn số 2: Ta di chuyển 2 vạch về bên phải số 0.
- Biểu diễn tương tự với các số nguyên dương còn lại.
Về bên trái số 0 biểu diễn các số -1; -2; -3; …
- Biểu diễn số - 1: Ta di chuyển 1 vạch về bên trái số 0.
- Biểu diễn số - 2: Ta di chuyển 2 vạch về bên phải số 0.
- Biểu diễn tương tự với các số nguyên âm còn lại.
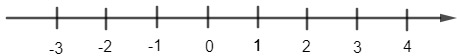
Hoạt động 4

Trên trục số, mỗi điểm 6; -6 cách điểm 0 bao nhiêu đơn vị?
Gợi ý đáp án:
Quan sát trục số, ta thấy số 6 cách số 0 sáu khoảng về bên phải nên điểm 6 cách 0 sáu đơn vị.
Số - 6 cũng cách số 0 sáu khoảng về bên trái nên điểm – 6 cách 0 sáu đơn vị.
Giải Toán 6 Chân trời sáng tạo phần Thực hành
Thực hành 1
Hãy đọc các số nguyên âm chỉ nhiệt độ dưới 0OC sau đây: -4OC, -10OC, -23OC.
Gợi ý đáp án:
-4OC đọc là: âm bốn độ C (hoặc trừ bốn độ C)
-10OC đọc là: âm mười độ C (hoặc trừ mười độ C)
-23OC đọc là: âm hai mươi ba độ C (hoặc trừ hai mươi ba độ C)
Thực hành 2
Các phát biểu sau đúng hay sai? Nếu sai hãy phát biểu lại cho đúng.
a) -4 ∈ Z; b) 5 ∈ Z; c) 0 ∈ Z;
d) -8 ∈ N; e) 6 ∈ N; f) 0 ∈ N;
Gợi ý đáp án:
a) – 4 là số nguyên âm nên – 4 thuộc Z. Do đó -4 ∈ Z là đúng.
b) 5 là số nguyên dương nên 5 thuộc Z. Do đó 5 ∈ Z là đúng.
c) 0 là một phần tử của tập hợp Z nên 0 ∈ Z là đúng.
d) – 8 là số nguyên âm nên – 8 không thuộc N nên là sai, viết lại
e) 6 là một số tự nhiên N nên 6 ∈ N là đúng.
f) 0 là một số tự nhiên N nên 0 ∈ N là đúng.
Thực hành 3
Hãy nói độ cao hoặc độ sâu của các địa danh sau:

Gợi ý đáp án:
Độ cao của đỉnh Phan – xi – păng là 3 143 m.
Độ cao của đáy vịnh Cam Ranh là – 32 m hay độ sâu của đáy vịnh Cam Ranh là 32 m.
Độ cao của đỉnh Everest là 8 848 m.
Độ cao của đáy khe Mariana là – 10 994 m hay độ sâu đáy khe Mariana là 10 994 m.
Độ cao của đáy sông Sài Gòn là – 20 m hay độ sâu của đáy sông Sài Gòn là 20m.
Thực hành 4
Hãy vẽ và biểu diễn các số -1; -5; 1; 5; -4 trên trục số đó.
Đáp án
Ta biểu diễn các số trên trục số như sau:
- Biểu diễn số -1: Ta di chuyển 1 vạch về bên trái số 0.
- Biểu diễn số - 5: Ta di chuyển 5 vạch về bên trái số 0.
- Biểu diễn số 1: Ta di chuyển 1 vạch về bên phải số 0.
- Biểu diễn số 5: Ta di chuyển 5 vạch về bên phải số 0.
- Biểu diễn số - 4: Ta di chuyển 4 vạch về bên trái số 0.
Khi đó, ta được trục số như sau:

Ngoài ra ta cũng có thể vẽ trục số thẳng đứng như trong hình bên dưới.
Do đó chiều dưới lên trên từ điểm 0 là chiều dương, chiều từ trên xuống dưới từ điểm 0 là chiều âm của trục số.
Thực hành 5
Tìm số đối của mỗi số sau: 5; -4; -10; 2 020
Đáp án
| Số nguyên a | Số đối của số nguyên a |
| 5 | -5 |
| -4 | 4 |
| -10 | 10 |
| 2 020 | -2 020 |
Giải Toán 6 Chân trời sáng tạo phần Vận dụng
a) Mẹ Lan bán rau ở chợ, Lan giúp mẹ ghi số tiền lãi, lỗ hằng ngày trong một tuần như sau:

Hãy nêu các số nguyên chỉ số tiền lãi, lỗ mỗi ngày trong tuần.
b) Một nhà giàn DK1 trên vùng biển Đông của Việt Nam có 3 tầng trên mặt nước và 3 phần hệ thống chân đỡ có độ cao như sau:

Hãy nêu các số nguyên chỉ độ cao của mỗi bộ phận nhà giàn.
Gợi ý đáp án:
a) Các số nguyên chỉ số tiền lãi, lỗ mỗi ngày trong tuần là
Ngày 3/9: Số tiền lãi được biểu diễn là 200 (nghìn đồng);
Ngày 4/9: Số tiền lỗ được biểu diễn là -50 (nghìn đồng);
Ngày 5/9: Số tiền lãi được biểu diễn là 180 (nghìn đồng);
Ngày 6/9: Số tiền lãi được biểu diễn là 90 (nghìn đồng);
Ngày 7/9: Số tiền lỗ được biểu diễn là – 80 (nghìn đồng);
Ngày 8/9: Số tiền hòa vốn được biểu diễn là 0 (nghìn đồng)
Ngày 9/9: Số tiền lãi được biểu diễn là 140 (nghìn đồng).
b) Vì nhà giàn có 3 tầng trên mặt nước và 3 phần chân đỡ ở dưới mặt nước nên:
Độ cao của mỗi bộ phận nhà giàn là:
Độ cao phần 3 chân đỡ: -15 m;
Độ cao phần 2 chân đỡ: - 9 m;
Độ cao phần 1 chân đỡ: - 4 m;
Độ cao tầng 1: 8 m;
Độ cao tầng 2: 18 m;
Độ cao tầng 3: 25 m.
Giải Toán 6 Chân trời sáng tạo trang 53, 54 tập 1
Bài 1
Dùng số nguyên thích hợp để diễn tả các tình huống sau:
a) Thưởng 5 điểm trong một cuộc thi đấu;
b) Bớt 2 điểm vì phạm luật;
c) Tăng 1 bậc lương do làm việc hiệu quả.
d) Hạ 2 bậc xếp loại do thi đấu kém.
Gợi ý đáp án:
a) 5
b) – 2
c) 1
d) - 2
Bài 2
Các phát biểu sau đây đúng hay sai?
a) 9 ∈ N;
d) 0 ∈ Z;
b) -6 ∈ N;
e) 5 ∈ Z;
c) - 3 ∈ Z;
g) 20 ∈ N.
Gợi ý đáp án:
a) Đúng
d) Đúng
b) Sai
e) Đúng
c) Đúng
g) Đúng
Bài 3
Số nguyên nào thích hợp cho các ô trống sau:
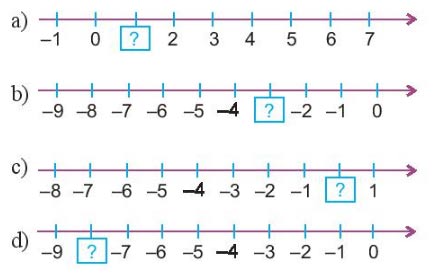
Gợi ý đáp án:
a) 1
b) – 3
c) 0
d) – 8
Bài 4
Vẽ một đoạn trục số từ - 10 đến 10. Biểu diễn các số nguyên sau đây:
+ 5; -4; 0; - 7; - 8; 2; 3; 9; - 9.
Gợi ý đáp án:
Trục số biểu diễn các số như sau:
![]()
Bài 5
Hãy vẽ một trục số, rồi vẽ trên đó những điểm nằm cách điểm 0 hai đơn vị. Những điểm này biểu diễn các số nguyên nào?
Gợi ý đáp án:

Những điểm A, B nằm cách điểm 0 hai đơn vị biểu diễn các số nguyên 2 và – 2.
Bài 6
Tìm số đối của các số nguyên sau: - 5; - 10; 4; - 4; 0; - 100; 2 021.
Gợi ý đáp án:
Số đối của – 5 là 5.
Số đối của – 10 là 10.
Số đối của 4 là - 4.
Số đối của 0 là 0.
Số đối của – 100 là 100.
Số đối của 2 021 là – 2 021
- Lượt tải: 63
- Lượt xem: 34.449
- Dung lượng: 310,2 KB
Link Download chính thức:
Toán 6 Bài 1: Số nguyên âm và tập hợp các số nguyên Download-
 Quỳnh anh NguyễnThích · Phản hồi · 3 · 11/11/22
Quỳnh anh NguyễnThích · Phản hồi · 3 · 11/11/22 -
 Chihao TranThích · Phản hồi · 2 · 15/11/22
Chihao TranThích · Phản hồi · 2 · 15/11/22










 Toán 6 CTST
Toán 6 CTST 