Download.vn Học tập Lớp 11 Toán 11 Cánh Diều

Toán 11 Bài 1: Đường thẳng và mặt phẳng trong không gian Giải Toán 11 Cánh diều trang 85, 86, 87, 88, ... 94

Tải về Bình luận
  • 1
Mục lục

Toán lớp 11 tập 1 trang 85, 86, 87, 88, ... 94 Cánh diều là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 11 tham khảo.

Giải Toán 11 Cánh diều Bài 1 Đường thẳng và mặt phẳng trong không gian được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 94. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết Toán 11 tập 1 Bài 1 Đường thẳng và mặt phẳng trong không gian Cánh diều, mời các bạn cùng theo dõi tại đây.

Giải Toán 11 Bài 1: Đường thẳng và mặt phẳng trong không gian

Toán lớp 11 tập 1 trang 94 - Cánh diều

Bài 1 trang 94

Khi trát tường, dụng cụ không thể thiếu của người thợ là thước dẹt dài (Hình 28). Công dụng của thước dẹt này là gì? Giải thích.

Gợi ý đáp án

Thước dẹt làm cho mặt lớp vữa phẳng và dải mốc cùng nằm trên mặt phẳng.

Bài 2 trang 94

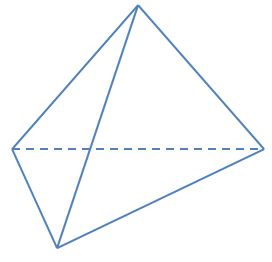
Hình 29 là hình ảnh của chặn giấy bằng gỗ có bốn mặt phân biệt là các tam giác. Vẽ hình biểu diễn của chặn giấy bằng gỗ đó.

Gợi ý đáp án

Bài 3 trang 94

Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng và đôi một cắt nhau. Chứng minh rằng ba đường thẳng a, b, c cùng đi qua một điểm, hay còn gọi là ba đường thẳng đồng quy.

Gợi ý đáp án

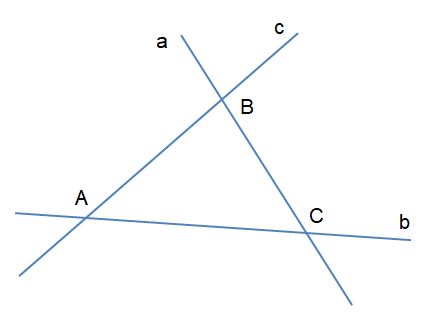
Giả sử: Đường thẳng a và b cắt nhau tại C.

Đường thẳng a và c cắt nhau tại B.

Đường thẳng b và c cắt nhau tại A.

trong đó, A, B, C không đồng quy (1)

Khi đó: B và C thuộc đường thẳng A

Mặt khác: B thuộc đường thẳng c, C thuộc đường thẳng b

Suy ra: BC thuộc mp chứa đường thẳng b và c.

Do đó: Đường thẳng a thuộc mp (b,c) nên ba đường thẳng này đồng quy (trái với (1)).

Kết luận: Ba đường thẳng a, b, c cùng đi qua một điểm.

Bài 4 trang 94

Cho hình chóp S.ABCD có AC cắt BD tại O và AB cắt CD tại P. Điểm M thuộc cạnh SA (M khác S, M khác A). Gọi N là giao điểm của MP và SB, I là giao điểm của MC và DN. Chứng minh rằng S, O, I thẳng hàng.

Gợi ý đáp án

Ta có: DN thuộc (SBD) và MC thuộc (SAC)

Mà MC cắt DN tại I nên I là giao điểm của (SBD) và (SAC).

Ta có: S và O cùng thuộc hai mặt phẳng (SBD) và (SAC).

Theo tính chất 4: Các điểm S, O, I đều thuộc giao điểm của hai mặt phẳng (SBD) và (SAC).

Vậy ba điểm S, O, I thẳng hàng.

Bài 5 trang 94

Cho hình chóp S.ABC. Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho MA= 2MS, NS = 2NC.

a) Xác định giao điểm của MN với mặt phẳng (ABC).

b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC).

Gợi ý đáp án

a) △SAC có: MN cắt AC tại E mà AC thuộc (ABC)

Do đó: E là giao điểm của MN và (ABC).

b) Ta có: B thuộc hai mặt phẳng (BMN) và (ABC)

E thuộc hai mặt phẳng (BMN) và (ABC)

Suy ra: BE là giao tuyến của hai mặt phẳng trên.

Bài 6 trang 94

Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi M là trung điểm của SA.

a) Xác định giao điểm của CD với mặt phẳng (SAB).

b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).

c) Xác định giao tuyến của hai mặt phẳng (MCD) và (SBC).

Gợi ý đáp án

a) Gọi E là giao điểm của AB và CD

Vì AB thuộc mặt phẳng (SAB) nên E là giao điểm của CD và (SAB).

b) Ta có: S thuộc hai mặt phẳng (SAB) và (SCD).

E thuộc hai mặt phẳng (SAB) và (SCD).

Suy ra: SE là giao tuyến của hai mặt phẳng trên.

c) Trong (SAB), gọi G là giao điểm của ME và SB.

Mà SB thuộc (SBC), ME thuộc (MCD).

Do đó, G thuộc hai mặt phẳng (MCD) và (SBC).

Ta có: C thuộc hai mặt phẳng (MCD) và (SBC).

Vậy CG là giao tuyến của hai mặt phẳng trên.

Bài 7 trang 94

Cho hình tứ diện ABCD. Gọi I là trung điểm cạnh CD. Gọi M, N lần lượt là trọng tâm các tam giác BCD, CDA.

a) Chứng minh rằng các điểm M, N thuộc mặt phẳng (ABI).

b) Gọi G là giao điểm của AM và BN. Chứng minh rằng: \frac{GM}{GA}=\frac{GN}{GB}=\frac{1}{3}.

c) Gọi P, Q lần lượt là trọng tâm các tam giác DAB, ABC. Chứng minh rằng các đường thẳng CP, DQ cùng đi qua điểm G và \frac{GP}{GC}=\frac{GQ}{GD}=\frac{1}{3}.

Gợi ý đáp án

a) Ta có: M là trọng tâm của \triangleBCD, mà I là trung điểm của CD

Nên: M nằm trên trung tuyến BI (1)

Ta có: N là trọng tâm của \triangleACD, mà I là trung điểm của CD

Nên: N nằm trên trung tuyến AI (2)

Từ (1)(2) suy ra: M và N thuộc (ABI).

b) Gọi H, K lần lượt là trung điểm của AG, BG.

Ta có: HK // AB

Mà AB // MN

Suy ra: MN // HK.

Theo định lý Ta-lét, ta có: \frac{GM}{GH}=\frac{GN}{GK}=\frac{MN}{HK} (1)

Ta có: \frac{HK}{AB}=\frac{1}{2}, \frac{MN}{AB}=\frac{1}{3}

Do đó: \frac{MN}{AB}:\frac{HK}{AB}=\frac{2}{3}\Rightarrow \frac{MN}{HK}=\frac{2}{3} (2)

(1)(2) suy ra: \frac{GM}{GH}=\frac{2}{3} GH=\frac{1}{2}GA \Rightarrow \frac{GM}{\frac{1}{2}GA}=\frac{2}{3}\Rightarrow \frac{GM}{GA}=\frac{1}{3}

Chứng minh tương tự ta được: \frac{GN}{GB}=\frac{1}{3}.

c) Gọi H, K lần lượt là trung điểm của BC, BD

\triangleAHD có: \frac{HM}{HD}=\frac{HQ}{HA}=\frac{1}{3}

Suy ra: QM // AD

Do đó: \triangleQGM đồng dạng với \triangleDGA

Nên D, G, Q thẳng hàng

Ta có: QM// AD nên \frac{QM}{AD}=\frac{HM}{HD}=\frac{HQ}{HA}=\frac{1}{3}

Mà \frac{QM}{AD}=\frac{QG}{GD}

Do đó: \frac{QG}{GD}=\frac{1}{3}

Chứng minh tương tự ta được: \frac{GP}{GC}=\frac{1}{3}

Suy ra điều cần chứng minh.

Chia sẻ bởi: 👨 Trịnh Thị Thanh
Mời bạn đánh giá!
  • Lượt tải: 05
  • Lượt xem: 90
  • Dung lượng: 156,5 KB
Tìm thêm: Toán lớp 11 Toán 11 Giải SGK Toán 11 Cánh diều
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần

    Toán 11 - Cánh Diều