Toán 11 Bài 3: Hàm số liên tục Giải Toán 11 Cánh diều trang 73, 74, 75, 76, 77

Bài trước

Mục lục

Bài sau

Toán lớp 11 tập 1 trang 73, 74, 75, 76, 77 Cánh diều là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 11 tham khảo.

Giải Toán 11 Cánh diều Bài 3 Hàm số liên tục được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 77. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết Toán 11 tập 1 Bài 3 Hàm số liên tục trang 77 Cánh diều, mời các bạn cùng theo dõi tại đây.

Giải Toán 11 Bài 3: Hàm số liên tục

Toán lớp 11 tập 1 trang 77 - Cánh diều

Toán lớp 11 tập 1 trang 77 - Cánh diều

Bài 1 trang 77

Dùng định nghĩa xét tính liên tục của hàm số $f(x)=2x^{3}+x+1$ $f(x)=2x^{3}+x+1$ tại điểm $x=2$.

Gợi ý đáp án

Tập xác định: $\mathbb{R}$ $\mathbb{R}$

Ta có: $f(2)=2.2^{3}+2+1=19$ $f(2)=2.2^{3}+2+1=19$

$\lim_{x\rightarrow 2} f(x)=19$ $\lim_{x\rightarrow 2} f(x)=19$

Do đó: $\lim_{x\rightarrow 2} f(x)=f(2)$ $\lim_{x\rightarrow 2} f(x)=f(2)$

Vậy hàm số đã cho liên tục tại $x=2$.

Bài 2 trang 77

Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.

Gợi ý đáp án

a) $f(x)$ là hàm đa thức nên liên tục trên $\mathbb{R}$ $\mathbb{R}$.

b) TXĐ: $\mathbb{R}\setminus \left \{ 1 \right \}$ $\mathbb{R}\setminus \left \{ 1 \right \}$

Do hàm số $g(x)$ là hàm phân thức hữu tỉ nên hàm số liên tục trên mỗi khoảng $(-\infty,1)$ $(-\infty,1)$ và $(1,+\infty)$ $(1,+\infty)$.

c) Ta có: $\lim_{x\rightarrow -1^{-}} h(x)=\lim_{x\rightarrow -1^{-}}(-2x)=2$ $\lim_{x\rightarrow -1^{-}} h(x)=\lim_{x\rightarrow -1^{-}}(-2x)=2$

$\lim_{x\rightarrow -1^{+}} h(x)=\lim_{x\rightarrow -1^{+}}(x+1)=0$ $\lim_{x\rightarrow -1^{+}} h(x)=\lim_{x\rightarrow -1^{+}}(x+1)=0$

$h(-1)=-1+1=0$

Do đó: $\lim_{x\rightarrow -1^{-}} h(x)\neq \lim_{x\rightarrow -1^{+}} h(x)=h(-1)$ $\lim_{x\rightarrow -1^{-}} h(x)\neq \lim_{x\rightarrow -1^{+}} h(x)=h(-1)$

Vậy hàm số $h(x)$ không liên tục tại $x=-1$.

Bài 3 trang 77

Bạn Nam cho rằng: "Nếu hàm số $y=f(x)$ liên tục tại điểm $x_{0}$ $x_{0}$, còn hàm số $y=g(x)$ không liên tục tại $x_{0}$ $x_{0}$, thì hàm số $y=f(x)+g(x)$ không liên tục tại $x_{0}$ $x_{0}$". Theo em, ý kiến của bạn Nam đúng hay sai? Giải thích.

Gợi ý đáp án

Ý kiến đúng.

Giả sử $y=f(x)+g(x)$ liên tục tại $x_{0}$ $x_{0}$.

Đặt $h(x)=f(x)+g(x)$. Ta có: $g(x)=h(x)-f(x)$

Vì $y=h(x), y=f(x)$ liên tục tại $x_{0}$ $x_{0}$ nên hiệu của chúng là hàm số $y=g(x)$ phải liên tục tại $x_{0}$ $x_{0}$.

Điều này trái với đề bài nên do đó ý kiến của Nam là đúng.

Bài 4 trang 77

Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:

a) $f(x)=x^{2}+\sin x$ $f(x)=x^{2}+\sin x$;

b) $g(x)=x^{4}-x^{2}+\frac{6}{x-1}$ $g(x)=x^{4}-x^{2}+\frac{6}{x-1}$;

c) $h(x)=\frac{2x}{x-3}+\frac{x-1}{x+4}$ $h(x)=\frac{2x}{x-3}+\frac{x-1}{x+4}$.

Gợi ý đáp án

a) Ta có: $y=x^{2}$ $y=x^{2}$ là hàm đa thức nên liên tục trên $\mathbb{R}$ $\mathbb{R}$.

$y=\sin x$ $y=\sin x$ là hàm lượng giác nên liên tục trên $\mathbb{R}$ $\mathbb{R}$.

Do đó: Hàm số $f(x)=x^{2}+\sin x$ $f(x)=x^{2}+\sin x$ liên tục trên $\mathbb{R}$ $\mathbb{R}$.

b) TXĐ: $\mathbb{R}\setminus \left \{ 1 \right \}$ $\mathbb{R}\setminus \left \{ 1 \right \}$

Ta có: $y=x^{4}-x^{2}$ $y=x^{4}-x^{2}$ là hàm đa thức nên liên tục trên $\mathbb{R}$ $\mathbb{R}$.

Do đó: Hàm số $g(x)=x^{4}-x^{2}+\frac{6}{x-1}$ $g(x)=x^{4}-x^{2}+\frac{6}{x-1}$ liên tục trên mỗi khoảng $(-\infty,1)$ $(-\infty,1)$ và $(1,+\infty)$ $(1,+\infty)$.

c) TXĐ: $\mathbb{R}\setminus \left \{ 3;-4 \right \}$ $\mathbb{R}\setminus \left \{ 3;-4 \right \}$

Hàm số $h(x)=\frac{2x}{x-3}+\frac{x-1}{x+4}$ $h(x)=\frac{2x}{x-3}+\frac{x-1}{x+4}$ liên tục trên mỗi khoảng $(-\infty,-4)$ $(-\infty,-4)$, $(-4,3)$ và $(3,+\infty)$ $(3,+\infty)$.

Bài 5 trang 77

Cho hàm số

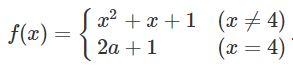a) Với $a=0$, xét tính liên tục của hàm số tại $x=4$.

b) Với giá trị nào của $a$ thì hàm số liên tục tại $x=4$?

c) Với giá trị nào của $a$ thì hàm số liên tục trên tập xác định của nó?

Gợi ý đáp án

a) Ta có: a=0 thì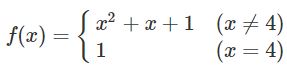

Có: $f(4)=1$

$\lim_{x\rightarrow 4} f(x)=4^{2}+4+1=21$ $\lim_{x\rightarrow 4} f(x)=4^{2}+4+1=21$

Do đó: $\lim_{x\rightarrow 4} f(x)\neq f(4)$ $\lim_{x\rightarrow 4} f(x)\neq f(4)$

Vậy hàm số không liên tục tại $x=4$.

b) Ta có: $f(4)=2a+1$

$\lim_{x\rightarrow 4} f(x)=4^{2}+4+1=21$ $\lim_{x\rightarrow 4} f(x)=4^{2}+4+1=21$

Để hàm số liên tục tại $x=4$ thì: $2a+1=21\Leftrightarrow a=10$ $2a+1=21\Leftrightarrow a=10$.

Vậy $a=10$ thì hàm số liên tục tại $x=4$.

c) TXĐ: $\mathbb{R}$ $\mathbb{R}$

Do $f(x)=x^{2}+x+1$ $f(x)=x^{2}+x+1$ nếu $x\neq 4$ $x\neq 4$ nên hàm số liên tục trên mỗi khoảng $(-\infty,4)$ $(-\infty,4)$ và $(4,+\infty)$ $(4,+\infty)$.

Nếu $a=10$ thì hàm số liên tại điểm $x=4$.

Do đó khi $a=10$ thì hàm số liên tục trên $\mathbb{R}$ $\mathbb{R}$.

Bài 6 trang 77

Hình 16 biểu thị độ cao $h$ (m) của một quả bóng được đá lên theo thời gian $t$ (s), trong đó $h(t)=-2t^{2}+8t$ $h(t)=-2t^{2}+8t$.

a) Chứng tỏ hàm số $h(t)$ liên tục trên tập xác định.

b) Dựa vào đồ thị hãy xác định $\lim_{t\rightarrow 2}(-2t^{2}+8t)$ $\lim_{t\rightarrow 2}(-2t^{2}+8t)$.

Gợi ý đáp án

a) Ta có: $h\geq 0,t\geq 0\Rightarrow -2t^{2}+8t\geq 0\Leftrightarrow 0\leq t\leq 4$ $h\geq 0,t\geq 0\Rightarrow -2t^{2}+8t\geq 0\Leftrightarrow 0\leq t\leq 4$

Suy ra tập xác định hàm số là: $\left [ 0,4 \right ]$ $\left [ 0,4 \right ]$.

Vì hàm số là hàm đa thức nên hàm số liên tục trên đoạn $\left [ 0,4 \right ]$ $\left [ 0,4 \right ]$.

b) $\lim_{t\rightarrow 2} (-2t^{2}+8t)=8$ $\lim_{t\rightarrow 2} (-2t^{2}+8t)=8$

Chia sẻ bởi: