Toán 11 Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác Giải Toán 11 Cánh diều trang 5, 6, 7, 8 ....15

Giải Toán 11 Cánh diều Tập 1 trang 15 giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi hoạt động và 6 bài tập trong SGK bài Góc lượng giác Giá trị lượng giác của góc lượng giác được nhanh chóng và dễ dàng hơn.

Toán 11 Cánh diều trang 16 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh lớp 11 học tốt môn Toán 11. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 11 Cánh diều Tập 1 trang 16 mời các bạn cùng theo dõi.

Phần Hoạt động Toán 11 Bài 1 Cánh diều

Hoạt động 1

Nêu định nghĩa góc trong hình học phẳng.

Gợi ý đáp án

Góc (còn được gọi là góc hình học) là hình gồm hai tia chung gốc. Mỗi góc có một số đo, đơn vị đo góc (hình học) là độ . Số đo của một góc (hình học) không vượt quá 180°.

Hoạt động 2

So sánh chiều quay của kim đồng hồ với:

a) Chiều quay từ tia Om đến tia Ox trong Hình 3a.

b) Chiều quay từ tia Om đến tia Oy trong Hình 3b.

Gợi ý đáp án

a) Chiều quay từ tia Om đến tia Ox trong Hình 3a là chiều quay ngược chiều kim đồng hồ

b) Chiều quay từ tia Om đến tia Oy trong Hình 3b là chiều quay cùng chiều kim đồng hồ.

Hoạt động 3

a) Trong Hình 5a, tia Om quay theo chiều dương đúng một vòng. Hỏi tia đó quét nên một góc bao nhiêu độ?

b) Trong Hình 5b, tia Om quay theo chiều dương ba vòng và một phần tư vòng (tức là \(3\frac{1}{4}\)

vòng). Hỏi tia đó quét nên một góc bao nhiêu độ?

c) Trong Hình 5c, tia Om quay theo chiều âm đúng một vòng. Hỏi tia đó quét nên một góc bao nhiêu độ?

Gợi ý đáp án

a) Trong Hình 5a, tia Om quay theo chiều dương đúng một vòng nên tia đó quét nên một góc 360^o.

b) Trong Hình 5b, tia Om quay theo chiều dương ba vòng và một phần tư vòng (tức là \(3\frac{1}{4}\)

vòng) nên tia đó quét nên một góc: \(3\frac{1}{4} .360^{\circ} =1170^{\circ}\)

c) Trong Hình 5c, tia Om quay theo chiều âm đúng một vòng nên tia đó quét nên một góc - 360^o

Hoạt động 4

Trên Hình 7a, ba góc lượng giác có cùng tia đầu Ou và tia cuối Ov, trong đó Ou⊥Ov. Xác định số đo của góc lượng giác trong các hình 7b, 7c, 7d.

Trên Hình 7a, ba góc lượng giác có cùng tia đầu Ou và tia cuối Ov, trong đó Ou⊥Ov. Xác định số đo của góc lượng giác trong các hình 7b, 7c, 7d.

Gợi ý đáp án

a) Hình 7b: Số đo của góc lượng giác (Ou,Ov) là \(\frac{\pi}{2}\)

Hình 7c: Số đo của góc lượng giác (Ou,Ov) là: \(\frac{\pi}{2}+2\pi=\frac{5\pi}{2}\)

Hình 7d: Số đo của góc lượng giác (Ou,Ov) là: \(-\frac{3\pi}{2}\)

Phần Bài tập Toán 11 Cánh diều trang 15

Bài 1 trang 15 SGK Toán 11 Cánh diều

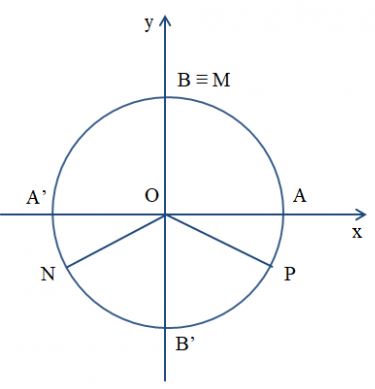
Xác định vị trí các điểm M, N, P trên đường tròn lượng giác sao cho số đo của các góc lượng giác (OA, OM), (OA, ON), (OA, OP) lần lượt bằng \(\frac{\pi }{2},\frac{7\pi }{6},\frac{-\pi }{6}\).

Gợi ý đáp án

Điểm M ≡ điểm B thì (OA, OM) = \(\frac{\pi }{2}\).

Điểm N nằm trên cung A'B', sao cho cung A'N = \(\frac{1}{3}\) cung A'B' thì (OA, ON) = \(\frac{7\pi }{6}\).

Điểm P nằm trên cung AB', sao cho cung AP = \(\frac{1}{3}\) cung AB' thì (OA, OP) = \(\frac{-\pi }{6}\).

Bài 2 trang 15 SGK Toán 11 Cánh diều

Tính các giá trị lượng giác của mỗi góc sau: 225^∘, −225^∘, −1035^∘, \(\frac{5\pi }{3}\), \(\frac{19\pi }{2}\), \(\frac{-159\pi }{4}\).

Gợi ý đáp án

sin(225^∘) = \(\frac{-\sqrt{2} }{2}\), cos(225^∘) = \(\frac{-\sqrt{2} }{2}\), tan(225^∘) = 1, cot(225^∘) = 1

sin(−225^∘) = \(\frac{\sqrt{2} }{2}\), cos(−225^∘) = \(\frac{\sqrt{2} }{2}\), tan(225^∘) = −1, cot(225^∘) = −1

sin (−1035^∘) = \(\frac{\sqrt{2} }{2}\), cos(−1035^∘) = \(\frac{\sqrt{2} }{2}\), tan(−1035^∘) = 1, cot(−1035^∘) = 1

sin(\(\frac{5\pi }{3}\)) = \(-\frac{\sqrt{3} }{2}\), cos(\(\frac{5\pi }{3}\)) = 12, tan(\(\frac{5\pi }{3}\)) = \(-\sqrt{3}\), cot(\(\frac{5\pi }{3}\)) = \(-\frac{\sqrt{3} }{3}\)

sin(\(\frac{19\pi }{2}\)) = −1, cos(\(\frac{19\pi }{2}\)) = 0, cot(\(\frac{19\pi }{2}\)) = 0

sin(\(\frac{-159\pi }{4}\)) = \(-\frac{\sqrt{2} }{2}\), cos(\(\frac{-159\pi }{4}\)) = \(\frac{\sqrt{2} }{2}\), tan(\(\frac{-159\pi }{4}\)) =−1, cot(\(\frac{-159\pi }{4}\)) = −1

Bài 3 trang 15 SGK Toán 11 Cánh diều

Tính các giá trị lượng giác (nếu có) của mỗi góc sau:

a) \(\frac{\pi }{3}\) + k2π (k∈Z);

b) kπ (k∈Z);

c) \(\frac{\pi }{2}\) + kπ (k∈Z);

d) \(\frac{\pi }{4}\) + kπ (k∈Z).

Gợi ý đáp án

a) sin(\(\frac{\pi }{3}\) + k2π) = \(\frac{\sqrt{3} }{2}\); cos (\(\frac{\pi }{3}\) + k2π)= \(\frac{1}{2}\); tan(\(\frac{\pi }{3}\) + k2π) = \(-\sqrt{3}\); cot(\(\frac{\pi }{3}\) + k2π) = \(\frac{\sqrt{3} }{3}\).

b) sin(kπ) = 0; cos(kπ) = −1 nếu k lẻ hoặc =1 nếu k chẵn; tan(kπ) = 0.

c) sin(\(\frac{\pi }{2}\) + kπ) = −1 nếu k lẻ hoặc =1 nếu k chẵn; cos(\(\frac{\pi }{2}\)+kπ) = 0; cot(\(\frac{\pi }{2}\)+kπ) = 0.

d) sin(\(\frac{\pi }{4}\) + kπ) = \(-\frac{\sqrt{2} }{2}\) nếu k lẻ hoặc = \(\frac{\sqrt{2} }{2}\) nếu k chẵn; cos(\(\frac{\pi }{4}\)+ kπ) = \(-\frac{\sqrt{2} }{2}\) nếu k lẻ hoặc = \(\frac{\sqrt{2} }{2}\) nếu k chẵn; tan(\(\frac{\pi }{4}\)+kπ) = 1; cot(\(\frac{\pi }{4}\)+kπ) = 1.

Bài 4 trang 15 SGK Toán 11 Cánh diều

Tính các giá trị lượng giác của góc α trong mỗi trường hợp sau:

a) sinα = \(\frac{\sqrt{15} }{4}\) với \(\frac{\pi }{2}\) < α < π;

b) cosα = \(-\frac{2}{3}\) với −π < α < 0;

c) tanα = 3 với −π < α < 0;

d) cotα = −2 với 0 < α < π.

Gợi ý đáp án

a) sinα = \(\frac{\sqrt{15} }{4}\) với \(\frac{\pi }{2}\) < α < π ⇒ α ≈ 1.318

b) cosα = \(-\frac{2}{3}\) với −π < α < 0⇒ α ≈ 2.3

c) tanα = 3 với −π < α < 0⇒ α ≈ 1.249

d) cotα =− 2 với 0 < α < π ⇒ α ≈ −0.464

Bài 5 trang 15 SGK Toán 11 Cánh diều

Tính:

a) A = sin²5^∘ + sin²10^∘ + sin²15^∘ +...+ sin²85^∘ (17 số hạng).

b) B = cos5^∘ + cos10^∘ + cos15^∘ +...+ cos175^∘ (35 số hạng).

Gợi ý đáp án

a) A = cos²85^∘ + cos²80^∘ + cos²75^∘ +...+ sin²45^∘ +...+ sin²85^∘ = \(\frac{17}{2}\)

b) B = −cos175^∘ − cos170^∘ − cos165^∘ −...+ cos175^∘ = 0

Bài 6 trang 15 SGK Toán 11 Cánh diều

Một vệ tinh được định vị tại vị trí A trong không gian. Từ vị trí A, vệ tinh bắt đầu chuyển động quanh Trái Đất theo quỹ đạo là đường tròn với tâm là tâm O của Trái Đất, bán kính 9000 km. Biết rằng vệ tinh chuyển động hết một vòng của quỹ đạo trong 2h.

a) Hãy tính quãng đường vệ tinh đã chuyển động được sau 1h; 3h; 5h.

b) Vệ tinh chuyển động được quãng đường 200 000 km sau bao nhiêu giờ (làm tròn kết quả đến hàng đơn vị)?

Gợi ý đáp án

Ta có công thức độ dài của một cung tròn là: l = R.α

a) Sau 1h, vệ tinh chuyển động được một cung α = π

Như vậy, quãng đường vệ tinh đã chuyển động được sau 1h là: l = 9000π (km).

Sau 3h, vệ tinh chuyển động được một cung α = 3π

Như vậy, quãng đường vệ tinh đã chuyển động được sau 3h là: l = 27000π (km).

Sau 5h, vệ tinh chuyển động được một cung α = 5π

Như vậy, quãng đường vệ tinh đã chuyển động được sau 5h là: l = 45000π (km).

b) Vệ tinh chuyển động được quãng đường 200 000 km sau: \(\frac{200000}{9000}\) ≈ 22h.

Lý thuyết Toán 11 Cánh diều Bài 1

1. Góc lượng giác