Download.vn Học tập Lớp 6 Đề thi học kì 1 Lớp 6 Đề thi

Bộ đề thi học kì 1 môn Toán 6 năm 2025 - 2026 sách Cánh diều 5 Đề thi cuối kì 1 Toán 6 (CV 7991, đáp án, ma trận)

Tải về Bình luận
  • 43
Mục lục

Đề thi học kì 1 môn Toán 6 Cánh diều năm 2025 - 2026 mang đến 5 đề kiểm tra có ma trận, đáp án hướng dẫn giải chi tiết, trình bày khoa học theo cấu trúc mới giúp thầy cô tham khảo thuận tiện.

TOP 5 Đề kiểm tra học kì 1 Toán 6 Cánh diều được biên soạn theo Công văn 7991 của Bộ GD&ĐT gồm trắc nghiệm lựa chọn đáp án đúng, trắc nghiệm đúng sai, trả lời ngắn và tự luận. Qua đó, giúp các em dễ dàng ôn tập, hệ thống kiến thức, luyện giải đề, rồi so sánh kết quả thuận tiện hơn. Bên cạnh đó, có thể tham khảo thêm đề thi giữa kì 1 môn Tin học, Khoa học tự nhiên. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn nhé:

Đề thi học kì 1 Toán 6 Cánh diều năm 2025 - 2026 (Công văn 7991)

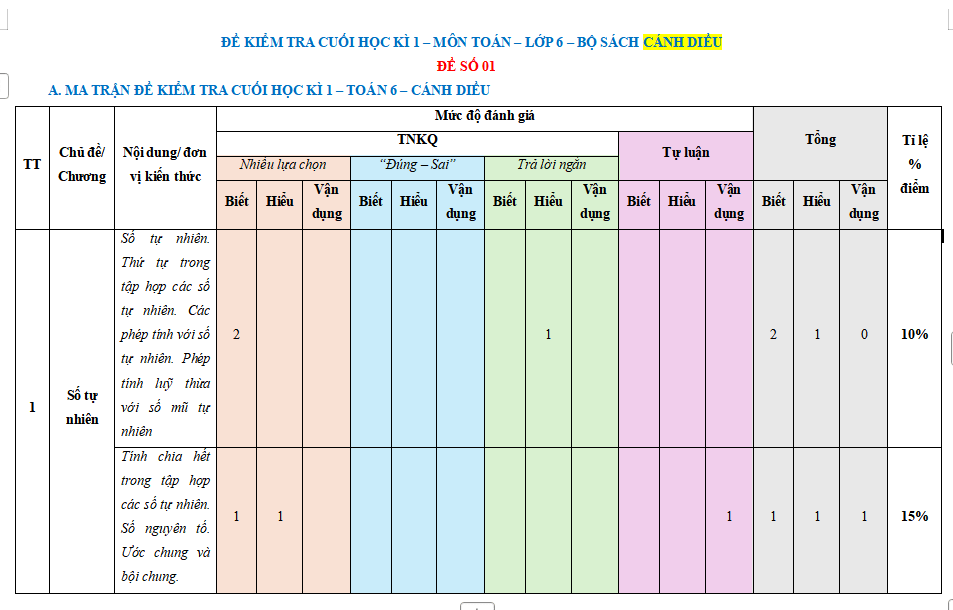
1. Ma trận đề thi học kì 1 Toán 6 Cánh diều

Ma trận đề thi học kì 1 Toán 6 Cánh diều

2. Đề thi học kì 1 Toán 6 Cánh diều

Đề thi học kì 1 Toán 6 Cánh diều

Đề thi học kì 1 Toán 6 Cánh diều

>> Nội dung đề thi vẫn còn trong file tải về

3. Đáp án đề kiểm tra học kì 1 Toán 6

>> Đáp án đề kiểm tra học kì 1 Toán 6 có trong file tải về

...........

>> Tải file để tham khảo trọn Bộ đề thi học kì 1 môn Toán 6 sách Cánh diều!

Chia sẻ bởi: 👨 Tiểu Hy

Chọn file cần tải:

Tìm thêm: Đề thi học kì 1 lớp 6 Cánh diều Cánh Diều Lớp 6

Nhiều người đang xem

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
👨

Tài liệu tham khảo khác

Chủ đề liên quan

KHO TÀI LIỆU GIÁO DỤC & HỖ TRỢ CAO CẤP

Mở khóa quyền truy cập vào hàng ngàn tài liệu độc quyền và nhận hỗ trợ nhanh chóng từ đội ngũ của chúng tôi.

Hỗ trợ tư vấn

Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu

Hotline

024 322 333 96

Có thể bạn quan tâm

Xem thêm

Mới nhất trong tuần

Tìm bài trong mục này

Tải nhanh tài liệu

Bộ đề thi học kì 1 môn Toán 6 năm 2025 - 2026 sách Cánh diều

Ưu đãi đặc biệt

Thông tin thanh toán nhanh

Bộ đề thi học kì 1 môn Toán 6 năm 2025 - 2026 sách Cánh diều

149.000đ

Hỗ trợ Zalo
Nhắn tin Zalo