Download.vn Học tập Lớp 10 Toán 10 Chân trời sáng tạo

Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180 Giải SGK Toán 10 trang 65 - Tập 1 sách Chân trời sáng tạo

Tải về Bình luận
  • 3
Mục lục

Toán 10 Chân trời sáng tạo tập 1 trang 65 là tài liệu vô cùng hữu ích, giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần mở đầu, thực hành và 7 bài tập được nhanh chóng và dễ dàng hơn.

Giải Toán 10 Chân trời sáng tạo trang 65 giúp các em nắm rõ kiến thức cơ bản trong bài học đầu tiên của Toán 10, tránh nhầm lẫn khi tiếp cận kiến thức mới. Giải Toán 10 trang 65 Chân trời sáng tạo hướng dẫn cách giải các bước giải cụ thể để học sinh biết cách trình bày lời giải khoa học, chính xác. Giúp các em học sinh hệ thống lại nội dung, dễ dàng đối chiếu kết quả, từ đó khắc sâu kiến thức. Vậy sau đây là trọn bộ nội dung Giải Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180 0 mời các bạn cùng theo dõi và tải tại đây.

Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180 0

Khởi động Toán 10 Bài 1 Chân trời sáng tạo

 Làm thế nào để mở rộng khái niệm tỉ số lượng giác của góc nhọn cho các góc từ 0° đến 180°? 

Gợi ý đáp án 

Để mở rộng khái niệm tỉ số lượng giác của góc nhọn cho góc từ 0° đến 180° ta thực hiện như sau:

Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho ˆ x O M = α . Gọi (x0; y0) là tọa độ của điểm M, ta có:

+ sin của góc α là tung độ y0 của điểm M, được kí hiệu là sinα;

+ côsin của góc α là hoành độ x0 của điểm M, được kí hiệu là cosα;

+ tang của α là tỉ số \frac{y_0}{x_0}\(\frac{y_0}{x_0}\) (x0 ≠ 0), được kí hiệu là tanα = \frac{y_0}{x_0}\(\frac{y_0}{x_0}\)

+ côtang của α là tỉ số \frac{x_0}{y_0}\(\frac{x_0}{y_0}\) (y0 ≠ 0), được kí hiệu là cotα = \frac{x_0}{y_0}\(\frac{x_0}{y_0}\)

Phần Thực hành Toán 10 Chân trời sáng tạo Bài 1

Thực hành 1

Tìm các giá trị lượng giác của góc 135 0

Gợi ý đáp án

Hình vẽ minh họa:

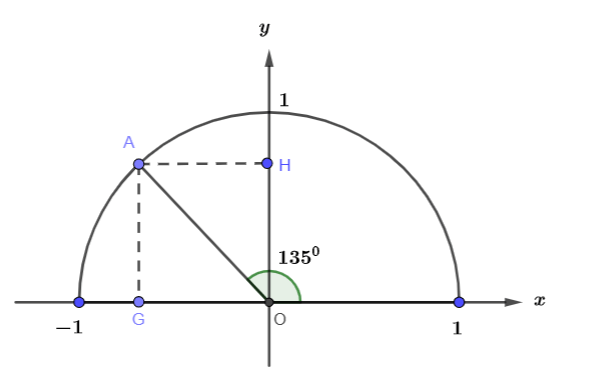
Lấy điểm A trên nửa đường tròn đơn vị sao cho \widehat {xOA} = {135^{0}}\(\widehat {xOA} = {135^{0}}\)

Ta có:

\widehat {yOA} = {180^0} - {135^0} = {45^0}\(\widehat {yOA} = {180^0} - {135^0} = {45^0}\)

Ta tính được tọa độ điểm A là A = \left( {\frac{{ - \sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right)\(A = \left( {\frac{{ - \sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right)\)

Vậy theo định nghĩa ta có:

\sin {135^0} = \frac{{\sqrt 2 }}{2}\(\sin {135^0} = \frac{{\sqrt 2 }}{2}\)

\cos{135^0} = -\frac{{\sqrt 2 }}{2}\(\cos{135^0} = -\frac{{\sqrt 2 }}{2}\)

\tan {135^0} =- 1\(\tan {135^0} =- 1\)

\cot {135^0} = -1\(\cot {135^0} = -1\)

Thực hành 2

Tính các giá trị lượng giác sin120 0 ; cos150 0 ; cot135 0 .

Gợi ý đáp án

Thực hiện phép tính ta có kết quả như sau:

sin1200 = sin (1800 – 1200) = sin600 = \frac{{\sqrt 3 }}{2}\(\frac{{\sqrt 3 }}{2}\)

cos1500 = -cos(1800 – 1500) = -cos 300 = -\frac{{\sqrt 3 }}{2}\(-\frac{{\sqrt 3 }}{2}\)

cot1350 = - cot(1800 – 1350) = -cot 450 = -1

Bài tập Toán 10 trang 65 Chân trời sáng tạo

Bài 1 trang 65 Toán 10 Chân trời sáng tạo

Cho biết \sin {30^o} = \frac{1}{2};\sin {60^o} = \frac{{\sqrt 3 }}{2};\tan {45^o} = 1\(\sin {30^o} = \frac{1}{2};\sin {60^o} = \frac{{\sqrt 3 }}{2};\tan {45^o} = 1\). Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của

E = 2\cos {30^o} + \sin {150^o} + \tan {135^o}.\(E = 2\cos {30^o} + \sin {150^o} + \tan {135^o}.\)

Gợi ý đáp án

Ta có:

\begin{array}{l}\cos {30^o} = \sin \left( {{{90}^o} - {{30}^o}} \right) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\sin {150^o} = \sin \left( {{{180}^o} - {{150}^o}} \right) = \sin {30^o} = \frac{1}{2};\\\tan {135^o} = - \tan \left( {{{180}^o} - {{135}^o}} \right) = - \tan {45^o} = - 1\end{array}\(\begin{array}{l}\cos {30^o} = \sin \left( {{{90}^o} - {{30}^o}} \right) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\sin {150^o} = \sin \left( {{{180}^o} - {{150}^o}} \right) = \sin {30^o} = \frac{1}{2};\\\tan {135^o} = - \tan \left( {{{180}^o} - {{135}^o}} \right) = - \tan {45^o} = - 1\end{array}\)

\Rightarrow E = 2.\frac{{\sqrt 3 }}{2} + \frac{1}{2} - 1 = \sqrt 3 - \frac{1}{2}.\(\Rightarrow E = 2.\frac{{\sqrt 3 }}{2} + \frac{1}{2} - 1 = \sqrt 3 - \frac{1}{2}.\)

Bài 2 trang 65 Toán 10 Chân trời sáng tạo

Chứng minh các hệ thức sau:

a) \sin {20^o} = \sin {160^o}\(a) \sin {20^o} = \sin {160^o}\)

b) \cos {50^o} = - \cos {130^o}\(b) \cos {50^o} = - \cos {130^o}\)

Gợi ý đáp án

a)

\sin {20^o} = \sin \left( {{{180}^o} - {{160}^o}} \right) = \sin {160^o}\(\sin {20^o} = \sin \left( {{{180}^o} - {{160}^o}} \right) = \sin {160^o}\)

b)

\cos {50^o} = \cos \;({180^o} - {130^o}) = - \cos {130^o}\(\cos {50^o} = \cos \;({180^o} - {130^o}) = - \cos {130^o}\)

Bài 3 trang 65 Toán 10 Chân trời sáng tạo

Tìm góc \alpha \;\;({0^o} \le \alpha \le {180^o})\(\alpha \;\;({0^o} \le \alpha \le {180^o})\) trong mỗi trường hợp sau:

a) \cos \alpha = - \frac{{\sqrt 2 }}{2}\(a) \cos \alpha = - \frac{{\sqrt 2 }}{2}\)

b) \sin \alpha = 0\(b) \sin \alpha = 0\)

c) \tan \alpha = 1\(c) \tan \alpha = 1\)

d) \cot \alpha\(\cot \alpha\) không xác định.

Gợi ý đáp án

a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \cos \alpha\(\cos \alpha\)ta có:

\cos \alpha = \frac{{ - \sqrt 2 }}{2} với \alpha = {135^o}\(\cos \alpha = \frac{{ - \sqrt 2 }}{2} với \alpha = {135^o}\)

b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \sin \alpha\(\sin \alpha\)ta có:

\sin \alpha = 0 với \alpha = {0^o} và \alpha = {180^o}\(\sin \alpha = 0 với \alpha = {0^o} và \alpha = {180^o}\)

c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \tan \alpha\(\tan \alpha\)ta có:

\tan \alpha = 1 với \alpha = {45^o}\(\tan \alpha = 1 với \alpha = {45^o}\)

d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \cot \alpha\(\cot \alpha\)ta có:

\cot \alpha\(\cot \alpha\)không xác định với \alpha = {0^o}\(\alpha = {0^o}\)

Bài 4 trang 65 Toán 10 Chân trời sáng tạo

Cho tam giác ABC. Chứng minh rằng:

a) \sin A = \sin \;(B + C)\(a) \sin A = \sin \;(B + C)\)

b) \cos A = - \cos \;(B + C)\(b) \cos A = - \cos \;(B + C)\)

Gợi ý đáp án

a)

\sin (B + C) = \sin \left( {{{180}^o} - A} \right) = \sin A\(\sin (B + C) = \sin \left( {{{180}^o} - A} \right) = \sin A\)

Vậy \sin A = \sin \;(B + C)\(\sin A = \sin \;(B + C)\)

b)

\cos (B + C) = \cos \left( {{{180}^o} - A} \right) = - \cos A\(\cos (B + C) = \cos \left( {{{180}^o} - A} \right) = - \cos A\)

Vậy \cos A = - \cos \;(B + C)\(\cos A = - \cos \;(B + C)\)

Bài 5 trang 65 Toán 10 Chân trời sáng tạo

Chứng minh rằng với mọi góc \alpha \;\;({0^o} \le \alpha \le {180^o}),\(\alpha \;\;({0^o} \le \alpha \le {180^o}),\) ta đều có:

Gợi ý đáp án

a) {\cos ^2}\alpha + {\sin ^2}\alpha = 1\(a) {\cos ^2}\alpha + {\sin ^2}\alpha = 1\)

Trên nửa đường tròn đơn vị, lấy điểm M sao cho \widehat {xOM} = \alpha\(\widehat {xOM} = \alpha\)

Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.

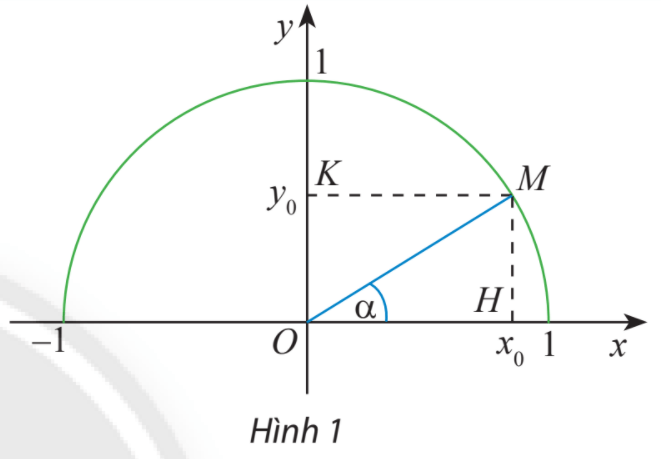
Ta có: tam giác vuông OHM vuông tại H và \alpha = \widehat {xOM}\(\alpha = \widehat {xOM}\)

Do đó: \sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.\(\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.\)

\Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1\(\Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1\)

b) \tan \alpha .\cot \alpha = 1\;({0^o} < \alpha < {180^o},\alpha \ne {90^o})\(\tan \alpha .\cot \alpha = 1\;({0^o} < \alpha < {180^o},\alpha \ne {90^o})\)

Ta có:

\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)

c) 1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\;(\alpha \ne {90^o})\(c) 1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\;(\alpha \ne {90^o})\)

Với \alpha \ne {90^o}\(\alpha \ne {90^o}\) ta có:

\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)

d) 1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\;({0^o} < \alpha < {180^o})\(d) 1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\;({0^o} < \alpha < {180^o})\)

Ta có:

\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\(\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)

Bài 6 trang 65 Toán 10 Chân trời sáng tạo

Cho góc \alpha\(\alpha\) với \cos \alpha = - \frac{{\sqrt 2 }}{2}\(\cos \alpha = - \frac{{\sqrt 2 }}{2}\). Tính giá trị của biểu thức A = 2{\sin ^2}\alpha + 5{\cos ^2}\alpha .\(A = 2{\sin ^2}\alpha + 5{\cos ^2}\alpha .\)

Gợi ý đáp án

Ta có: A = 2{\sin ^2}\alpha + 5{\cos ^2}\alpha = 2({\sin ^2}\alpha + {\cos ^2}\alpha ) + 3{\cos ^2}\alpha\(A = 2{\sin ^2}\alpha + 5{\cos ^2}\alpha = 2({\sin ^2}\alpha + {\cos ^2}\alpha ) + 3{\cos ^2}\alpha\)

Mà {\cos ^2}\alpha + {\sin ^2}\alpha = 1;\cos \alpha = - \frac{{\sqrt 2 }}{2}.\({\cos ^2}\alpha + {\sin ^2}\alpha = 1;\cos \alpha = - \frac{{\sqrt 2 }}{2}.\)

\Rightarrow A = 2 + 3.{\left( { - \frac{{\sqrt 2 }}{2}} \right)^2} = 2 + 3.\frac{1}{2} = \frac{7}{2}.\(\Rightarrow A = 2 + 3.{\left( { - \frac{{\sqrt 2 }}{2}} \right)^2} = 2 + 3.\frac{1}{2} = \frac{7}{2}.\)

Bài 7 trang 65 Toán 10 Chân trời sáng tạo

Dùng máy tính cầm tay, hãy thực hiện các yên cầu dưới đây:

a) Tính \sin {168^o}45\(\sin {168^o}45'33'';\cos {17^o}22'35'';\tan {156^o}26'39'';\cot {56^o}36'42''.\)

b) Tìm \alpha \;({0^o} \le \alpha \le {180^o})\(\alpha \;({0^o} \le \alpha \le {180^o})\),trong các trường hợp sau:

i) \sin \alpha = 0,862.\(i) \sin \alpha = 0,862.\)

ii) \cos \alpha = - 0,567.\(ii) \cos \alpha = - 0,567.\)

iii) \tan \alpha = 0,334.\(iii) \tan \alpha = 0,334.\)

Gợi ý đáp án

a)

\begin{array}{l}\sin {168^o}45\(\begin{array}{l}\sin {168^o}45'33'' = 0,195;\\\cos {17^o}22'35'' = 0,954;\\\tan {156^o}26'39'' = - 0,436;\\\cot {56^o}36'42'' = 0,659\end{array}\)

b)

i) \alpha = {59^o}32\(i) \alpha = {59^o}32'30,8''.\)

ii) \alpha = {124^o}32\(ii) \alpha = {124^o}32'28,65''.\)

iii) \alpha = {18^o}28\(iii) \alpha = {18^o}28'9,55''.\)

Chia sẻ bởi: 👨 Trịnh Thị Thanh
Liên kết tải về
Tìm thêm: Chân trời sáng tạo Chân trời sáng tạo Lớp 10

Nhiều người đang xem

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
👨

Tài liệu tham khảo khác

Chủ đề liên quan

KHO TÀI LIỆU GIÁO DỤC & HỖ TRỢ CAO CẤP

Mở khóa quyền truy cập vào hàng ngàn tài liệu độc quyền và nhận hỗ trợ nhanh chóng từ đội ngũ của chúng tôi.

Hỗ trợ tư vấn

Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu

Hotline

024 322 333 96

Có thể bạn quan tâm

Xem thêm

Mới nhất trong tuần

Tìm bài trong mục này
Đóng
Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ
Nhắn tin Zalo