Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn (không bao gồm tài liệu cao cấp) và trải nghiệm website không quảng cáo
Tìm hiểu thêm »Giải Toán 10 Bài 1: Hàm số và đồ thị giúp các em học sinh lớp 10 tham khảo, biết cách giải các bài tập trong SGK Toán 10 Tập 1 chương 3 trang 47 sách Chân trời sáng tạo.
Giải SGK Toán 10 chương 3 bài 1 sách Chân trời sáng tạo Tập 1 giúp các em học sinh nắm được cách trình bày, cách triển khai để giải được các bài tập trong sách giáo khoa. Từ đó các em học sinh tự bồi dưỡng và nâng cao kiến thức tự tin giải quyết tốt các bài tập. Đồng thời đây cũng là tư liệu hữu ích giúp thầy cô tham khảo để soạn giáo án cho riêng mình.
Tìm tập xác định của các hàm số sau:
![]() \(a) f(x) = \sqrt { - 5x + 3}\)
\(a) f(x) = \sqrt { - 5x + 3}\)
![]() \(b) f(x) = 2 + \frac{1}{{x + 3}}\)
\(b) f(x) = 2 + \frac{1}{{x + 3}}\)
Gợi ý đáp án
a) Biểu thức f(x) có nghĩa khi và chỉ khi ![]() \(- 5x + 3 \ge 0\),tức là khi
\(- 5x + 3 \ge 0\),tức là khi ![]() \(x \le \frac{3}{5}.\)
\(x \le \frac{3}{5}.\)
Vậy tập xác định của hàm số này là ![]() \(D = ( - \infty ;\frac{3}{5}]\)
\(D = ( - \infty ;\frac{3}{5}]\)
b) Biểu thức f(x) có nghĩa khi và chỉ khi ![]() \(x + 3 \ne 0\),tức là khi
\(x + 3 \ne 0\),tức là khi ![]() \(x \ne - 3\)
\(x \ne - 3\)
Vậy tập xác định của hàm số này là ![]() \(D = \mathbb{R}\backslash \left\{ { - 3} \right\}\)
\(D = \mathbb{R}\backslash \left\{ { - 3} \right\}\)
Tìm tập xác định, tập giá trị của hàm số có đồ thị như Hình 10.
Gợi ý đáp án
Từ đồ thị, ta có:
Đồ thị hàm số xác định (liền mạch) từ x = - 1 đến x = 9, do đó tập xác định của hàm số là D = [ - 1;9].
Tập giá trị ![]() \(T = \{ y|x \in [ - 1;9]\}\), vậy T = [ - 2;6]
\(T = \{ y|x \in [ - 1;9]\}\), vậy T = [ - 2;6]
Tìm các khoảng đồng biến, nghịch biến của các hàm số sau:
a) f(x) = - 5x + 2
b) ![]() \(f(x) = - {x^2}\)
\(f(x) = - {x^2}\)
Gợi ý đáp án
a) Xét hàm số y = - 5x + 2 xác định trên ![]() \(\mathbb{R}\)
\(\mathbb{R}\)
Lấy ![]() \({x_1},{x_2} \in \mathbb{R}\) là hai số tùy ý sao cho
\({x_1},{x_2} \in \mathbb{R}\) là hai số tùy ý sao cho![]() \({x_1} < {x_2}.\)
\({x_1} < {x_2}.\)
Do ![]() \({x_1} < {x_2} nên - 5{x_1} > - 5{x_2}\), suy ra
\({x_1} < {x_2} nên - 5{x_1} > - 5{x_2}\), suy ra ![]() \(- 5{x_1} + 2 > - 5{x_2} + 2\)
\(- 5{x_1} + 2 > - 5{x_2} + 2\)
Từ đây ta có f({x_1}) > f({x_2})
Vậy hàm số nghịch biến (giảm) trên ![]() \(\mathbb{R}\)
\(\mathbb{R}\)
b) Xét hàm số ![]() \(y = f(x) = - {x^2}\) xác định trên
\(y = f(x) = - {x^2}\) xác định trên ![]() \(\mathbb{R}\)
\(\mathbb{R}\)
+ Trên khoảng ![]() \((0; + \infty )\) lấy
\((0; + \infty )\) lấy ![]() \({x_1},{x_2} \in \mathbb{R}\) là hai số tùy ý sao cho
\({x_1},{x_2} \in \mathbb{R}\) là hai số tùy ý sao cho ![]() \({x_1} < {x_2}.\), ta có:
\({x_1} < {x_2}.\), ta có: ![]() \(f({x_1}) - f({x_2}) = - {x_1}^2 + {x_2}^2 = \left( {{x_2} - {x_1}} \right)({x_2} + {x_1})\)
\(f({x_1}) - f({x_2}) = - {x_1}^2 + {x_2}^2 = \left( {{x_2} - {x_1}} \right)({x_2} + {x_1})\)
Do ![]() \({x_1} < {x_2}\) nên
\({x_1} < {x_2}\) nên ![]() \({x_2} - {x_1} > 0\) và do
\({x_2} - {x_1} > 0\) và do ![]() \({x_1},{x_2} \in (0; + \infty ) nên {x_1} + {x_2} > 0.\)
\({x_1},{x_2} \in (0; + \infty ) nên {x_1} + {x_2} > 0.\)
Từ đây suy ra ![]() \(f({x_1}) - f({x_2}) > 0 hay f({x_1}) > f({x_2})\)
\(f({x_1}) - f({x_2}) > 0 hay f({x_1}) > f({x_2})\)
Vậy hàm số nghịch biến (giảm) trên khoảng ![]() \((0; + \infty )\)
\((0; + \infty )\)
+ Trên khoảng ![]() \(( - \infty ;0) lấy {x_1},{x_2} \in \mathbb{R}\) là hai số tùy ý sao cho
\(( - \infty ;0) lấy {x_1},{x_2} \in \mathbb{R}\) là hai số tùy ý sao cho ![]() \({x_1} < {x_2}.,\) ta có:
\({x_1} < {x_2}.,\) ta có:![]() \(f({x_1}) - f({x_2}) = - {x_1}^2 + {x_2}^2 = \left( {{x_2} - {x_1}} \right)({x_2} + {x_1})\)
\(f({x_1}) - f({x_2}) = - {x_1}^2 + {x_2}^2 = \left( {{x_2} - {x_1}} \right)({x_2} + {x_1})\)
Do ![]() \({x_1} < {x_2}\) nên
\({x_1} < {x_2}\) nên ![]() \({x_2} - {x_1} > 0\) và do
\({x_2} - {x_1} > 0\) và do ![]() \({x_1},{x_2} \in ( - \infty ;0)\) nên
\({x_1},{x_2} \in ( - \infty ;0)\) nên ![]() \({x_1} + {x_2} < 0.\)
\({x_1} + {x_2} < 0.\)
Từ đây suy ra ![]() \(f({x_1}) - f({x_2}) < 0 hay f({x_1}) < f({x_2})\)
\(f({x_1}) - f({x_2}) < 0 hay f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến (tăng) trên khoảng ![]() \(( - \infty ;0)\)
\(( - \infty ;0)\)
Vẽ đồ thị hàm số ![]() \(f\left( x \right) = \left| x \right|\) biết rằng hàm số này còn được viết như sau:
\(f\left( x \right) = \left| x \right|\) biết rằng hàm số này còn được viết như sau:
 \(f(x) = \left\{ \begin{array}{l}x\quad \quad (x \ge 0)\\ - x\quad \;\;(x < 0)\end{array} \right.\)
\(f(x) = \left\{ \begin{array}{l}x\quad \quad (x \ge 0)\\ - x\quad \;\;(x < 0)\end{array} \right.\)
Gợi ý đáp án
Hàm số ![]() \(f\left( x \right) = \left| x \right|\) xác định trên
\(f\left( x \right) = \left| x \right|\) xác định trên ![]() \(D = \mathbb{R}\)
\(D = \mathbb{R}\)
Trên khoảng ![]() \(( - \infty ;0)\) ta vẽ đồ thị hàm số y = - x, đi qua 2 điểm A( - 1;1),B( - 2;2)
\(( - \infty ;0)\) ta vẽ đồ thị hàm số y = - x, đi qua 2 điểm A( - 1;1),B( - 2;2)
Trên khoảng ![]() \((0; + \infty )\) ta vẽ đồ thị hàm số y = x, đi qua 2 điểm A'(1;1),B'(2;2)
\((0; + \infty )\) ta vẽ đồ thị hàm số y = x, đi qua 2 điểm A'(1;1),B'(2;2)
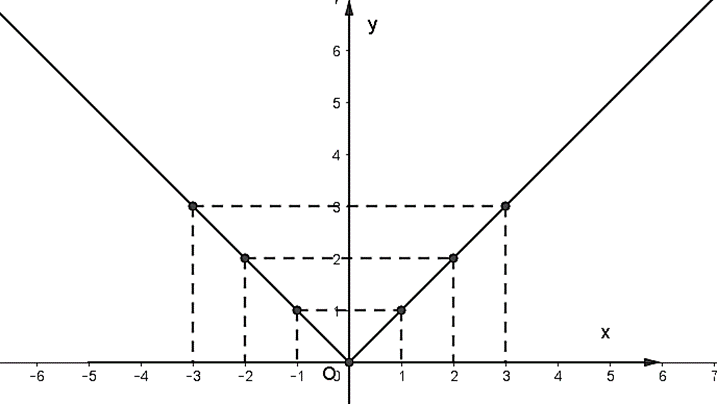
Như vậy ta được đồ thị hàm số ![]() \(f\left( x \right) = \left| x \right|.\)
\(f\left( x \right) = \left| x \right|.\)
Tìm tập xác định, tập giá trị và vẽ đồ thị hàm số:
![]() \(f(x) = \left\{ \begin{array}{l} - 1\quad \quad x < 0\\1\;\quad \quad \;{\kern 1pt} x > 0\end{array} \right.\quad\)
\(f(x) = \left\{ \begin{array}{l} - 1\quad \quad x < 0\\1\;\quad \quad \;{\kern 1pt} x > 0\end{array} \right.\quad\)
Gợi ý đáp án
+) Dễ thấy: hàm số được xác định với mọi x > 0 và x < 0.
Do đó tập xác định của hàm số là ![]() \(D = \mathbb{R}{\rm{\backslash }}\{ 0\}\)
\(D = \mathbb{R}{\rm{\backslash }}\{ 0\}\)
+) Với ![]() \(x \in D:\)
\(x \in D:\)
+ Nếu x > 0 thì f(x) = 1
+ Nếu x < 0 thì f(x) = - 1
Vậy tập giá trị của hàm số là ![]() \(T = \{ - 1;1\}\)
\(T = \{ - 1;1\}\)
+) Vẽ đồ thị hàm số:
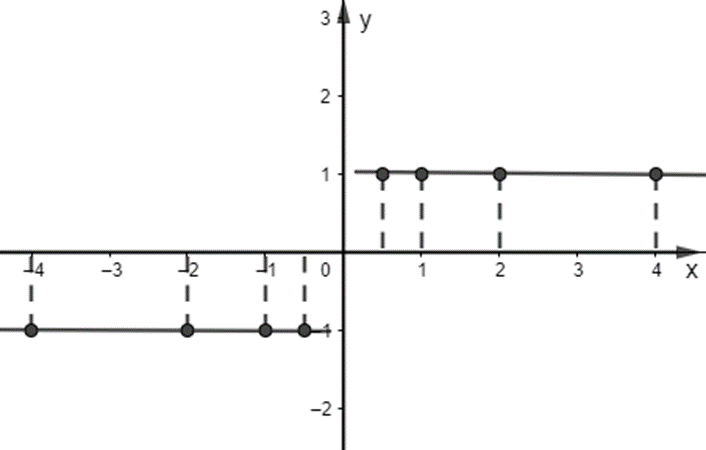
Với ![]() \(x \in ( - \infty ;0)\) đồ thị hàm số là đường thẳng y = - 1
\(x \in ( - \infty ;0)\) đồ thị hàm số là đường thẳng y = - 1
Với ![]() \(x \in (0; + \infty )\)) đồ thị hàm số là đường thẳng y = 1
\(x \in (0; + \infty )\)) đồ thị hàm số là đường thẳng y = 1
Ta được đồ thị hàm số như hình trên.
Một hãng taxi có bảng giá như sau:
|
Giá mở cửa (0,5 km) |
Giá cước các kilomet tiếp theo |
Giá cước từ kilomet thứ 31 |
|
|
Taxi 4 chỗ |
11 000 đồng |
14 500 đồng |
11 600 đồng |
|
Taxi 7 chỗ |
11 000 đồng |
15 500 đồng |
13 600 đồng |
a) Xem số tiền đi taxi là một hàm số phụ thuộc số kilomet di chuyển, hãy viết công thức của các hàm số dựa trên thông tin từ bảng giá đã cho theo từng yêu cầu:
i) Hàm số f(x) để tính số tiền hành khách phải trả khi di chuyển x km bằng xe taxi 4 chỗ.
ii) Hàm số g(x) để tính số tiền hành khách phải trả khi di chuyển x km bằng xe taxi 7 chỗ.
b) Nếu cần đặt xe taxi cho 30 hành khách, nên đặt toàn bộ xe 4 chỗ hay xe 7 chỗ thì có lợi hơn?
Gợi ý đáp án
a)
Nếu ![]() \(0,5 \le x < 31\) thì số tiền phải trả là 11000 + 14500.x đồng.
\(0,5 \le x < 31\) thì số tiền phải trả là 11000 + 14500.x đồng.
Nếu ![]() \(31 \le x\) thì số tiền phải trả là 11000 + 14500.30 + 11600.(x - 30) đồng.
\(31 \le x\) thì số tiền phải trả là 11000 + 14500.30 + 11600.(x - 30) đồng.
Vậy hàm số ![]() \(f(x) = \left\{ \begin{array}{l}11000 + 14500.x\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 0,5 \le x < 31\\11000 + 14500.30 + 11600.(x - 30)\;\quad \quad \;{\kern 1pt} x \ge 31\end{array} \right.\quad\)
\(f(x) = \left\{ \begin{array}{l}11000 + 14500.x\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 0,5 \le x < 31\\11000 + 14500.30 + 11600.(x - 30)\;\quad \quad \;{\kern 1pt} x \ge 31\end{array} \right.\quad\)
ii)
Nếu ![]() \(0,5 \le x < 31\) thì số tiền phải trả là 11000 + 15500.x đồng.
\(0,5 \le x < 31\) thì số tiền phải trả là 11000 + 15500.x đồng.
Nếu ![]() \(31 \le x\) thì số tiền phải trả là 11000 + 15500.30 + 13600.(x - 30) đồng.
\(31 \le x\) thì số tiền phải trả là 11000 + 15500.30 + 13600.(x - 30) đồng.
Vậy hàm số ![]() \(g(x) = \left\{ \begin{array}{l}11000 + 15500.x\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 0,5 \le x < 31\\11000 + 15500.30 + 13600.(x - 30)\;\quad \quad \;{\kern 1pt} x \ge 31\end{array} \right.\quad\)
\(g(x) = \left\{ \begin{array}{l}11000 + 15500.x\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 0,5 \le x < 31\\11000 + 15500.30 + 13600.(x - 30)\;\quad \quad \;{\kern 1pt} x \ge 31\end{array} \right.\quad\)
b)
Nếu đặt toàn bộ xe 4 chỗ cho 30 hành khách thì cần 8 xe.
Nếu đặt toàn bộ xe 7 chỗ cho 30 hành khách thì cần 5 xe.
So sánh số tiền dựa theo số kilomet di chuyển: Giả sử các hành khách cần di chuyển x kilomet
+) Nếu ![]() \(0,5 \le x < 31:\)
\(0,5 \le x < 31:\)
Số tiền trả cho 8 xe taxi 4 chỗ là: 8(11000 + 14500.x) = 88000 + 116000.x
Số tiền trả cho 5 xe taxi 7 chỗ là: 5(11000 + 15500.x) = 55000 + 77500.x
Vì 88000 + 116000.x > 55000 + 77500.x nên chọn 5 xe taxi 7 chỗ sẽ lợi hơn.
+) Nếu ![]() \(x \ge 31:\)
\(x \ge 31:\)
Số tiền trả cho 8 xe taxi 4 chỗ là: 8(11000 + 14500.30 + 11600.(x - 30)) = 784000 + 92800.x
Số tiền trả cho 5 xe taxi 7 chỗ là: 5(11000 + 15500.30 + 13600.(x - 30)) = 340000 + 68000x
Vì 784000 + 92800.x > 340000 + 68000.x nên chọn 5 xe taxi 7 chỗ sẽ lợi hơn.
Kết luận: Nên đặt toàn bộ xe 7 chỗ thì có lợi hơn.
Số 2 đã trải qua hành trình thú vị và bị biến đổi sau khi đi qua chiếc hộp đen. (Hình ảnh SGK)
Bác thợ máy đã giải mã hộp đen cho một số x bất kì như sau:
Bên trong hộp đen là một đoạn chương trình được cài đặt sẵn. Ta xem đoạn chương trình này như một hàm số f(x). Hãy viết biểu thức của f(x) để mô tả sự biến đổi đã tác động lên x.
Gợi ý đáp án
Sau khi vào hộp đen, x đi qua:
+) Đầu tiên, x đi qua hộp màu vàng (bình phương), ta được ![]() \({x^2}\)
\({x^2}\)
+) Tiếp tục,![]() \({x^2}\) đi qua hộp màu xanh lá (tăng gấp ba lần), ta được
\({x^2}\) đi qua hộp màu xanh lá (tăng gấp ba lần), ta được ![]() \(3{x^2}\)
\(3{x^2}\)
+) Cuối cùng, ![]() \(3{x^2}\) đi qua hộp màu xanh dương (bớt đi 5), ta được:
\(3{x^2}\) đi qua hộp màu xanh dương (bớt đi 5), ta được: ![]() \(3{x^2} - 5\)
\(3{x^2} - 5\)
Như vậy sau khi đi qua HỘP ĐEN, số x đã biến đổi thành số ![]() \(3{x^2} - 5\)
\(3{x^2} - 5\)
Kiểm tra lại với số 2: theo công thức thì sau khi qua hộp đen ta được số: ![]() \({3.2^2} - 5 = 7\)(đúng).
\({3.2^2} - 5 = 7\)(đúng).
Vậy biểu thức f(x) mô tả sự biến đổi đã tác động lên x là: f(x) = ![]() \(3{x^2} - 5.\)
\(3{x^2} - 5.\)
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: