Toán 11 Bài 3: Hàm số liên tục Giải Toán 11 Chân trời sáng tạo trang 80, 81, 82, 83, 84

Bài trước

Mục lục

Bài sau

Toán lớp 11 tập 1 trang 80, 81, 82, 83, 84, 85 Chân trời sáng tạo là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 11 tham khảo.

Giải Toán 11 Chân trời sáng tạo Bài 3 Hàm số liên tục được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 84, 85. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết Toán 11 tập 1 Bài 3 Hàm số liên tục Chân trời sáng tạo, mời các bạn cùng theo dõi tại đây.

Giải SGK Toán 11 Bài 3: Hàm số liên tục

I. Giải Toán 11 Chân trời sáng tạo trang 80, 81, 82, 83, 84
II. Luyện tập Hàm số liên tục

I. Giải Toán 11 Chân trời sáng tạo trang 80, 81, 82, 83, 84

Bài 1 trang 84

Xét tính liên tục của hàm số:

a) $f(x)=\left\{\begin{matrix}x^{2}+1; x \geq 0\\1-x; x<0\end{matrix}\right.$ $f(x)=\left\{\begin{matrix}x^{2}+1; x \geq 0\\1-x; x<0\end{matrix}\right.$ tại điểm x = 0

b) $f(x)=\left\{\begin{matrix}x^{2}+2; x \geq1\\ x; x<1\end{matrix}\right.$ $f(x)=\left\{\begin{matrix}x^{2}+2; x \geq1\\ x; x<1\end{matrix}\right.$ tại điểm x = 1

Gợi ý đáp án

a) $\lim_{x \to 0^{-}}f(x)=\lim_{x \to 0^{-}}(1-x)=1-0=1$ $\lim_{x \to 0^{-}}f(x)=\lim_{x \to 0^{-}}(1-x)=1-0=1$

$\lim_{x \to 0^{+}}f(x)=\lim_{x \to 0^{+}}(x^{2}+1)=0^{2}+1=1$ $\lim_{x \to 0^{+}}f(x)=\lim_{x \to 0^{+}}(x^{2}+1)=0^{2}+1=1$

Suy ra: $\lim_{x \to 0}f(x)= f(0)$ $\lim_{x \to 0}f(x)= f(0)$

Vậy hàm số y = f(x) liên tục tại x = 0

b) $\lim_{x \to 1^{-}}f(x)=\lim_{x \to 1^{-}}x=1$ $\lim_{x \to 1^{-}}f(x)=\lim_{x \to 1^{-}}x=1$

$\lim_{x \to 1^{+}}f(x)=\lim_{x \to 1^{+}}(x^{2}+2)=1^{2}+2=3$ $\lim_{x \to 1^{+}}f(x)=\lim_{x \to 1^{+}}(x^{2}+2)=1^{2}+2=3$

Suy ra không tồn tại $\lim_{x \to 1}f(x)$ $\lim_{x \to 1}f(x)$

Vậy hàm số y = f(x) không liên tục tại x = 1

Bài 2 trang 84

Cho hàm số $\left\{\begin{matrix}\frac{x^{2}-4}{x+2}; x \neq -2\\ a; x=-2\end{matrix}\right.$ $\left\{\begin{matrix}\frac{x^{2}-4}{x+2}; x \neq -2\\ a; x=-2\end{matrix}\right.$

Tìm a để hàm số y = f(x) liên tục trên $\mathbb{R}$ $\mathbb{R}$

Gợi ý đáp án

Ta có: $\lim_{x \to -2}f(x)=\lim_{x \to -2}\frac{x^{2}-4}{x+2} = \lim_{x \to -2}\frac{(x-2)(x+2)}{x+2} =\lim_{x \to -2}(x-2)=-2-2=-4$ $\lim_{x \to -2}f(x)=\lim_{x \to -2}\frac{x^{2}-4}{x+2} = \lim_{x \to -2}\frac{(x-2)(x+2)}{x+2} =\lim_{x \to -2}(x-2)=-2-2=-4$

f(-2) = a

Để hàm số f(x) liên tục trên $\mathbb{R}$ $\mathbb{R}$ thì hàm số f(x) phải liên tục tại $x_{0}=-2$ $x_{0}=-2$

Hay $\lim_{x \to -2}f(x) = f(-2)$ $\lim_{x \to -2}f(x) = f(-2)$

Suy ra: a = -4

Bài 3 trang 85

Xét tính liên tục của hàm số sau:

a) $f(x) = \frac{x}{x^{2}-4}$ $f(x) = \frac{x}{x^{2}-4}$

b) $g(x) = \sqrt{9-x^{2}}$ $g(x) = \sqrt{9-x^{2}}$

c) $h(x) = cosx + tanx$

Gợi ý đáp án

a) $f(x) = \frac{x}{x^{2}-4}$ $f(x) = \frac{x}{x^{2}-4}$ là hàm số phân thức có tập xác định là $(-\infty;2) \cup (2;+\infty)$ $(-\infty;2) \cup (2;+\infty)$

Nên hàm số f(x) liên tục trên các khoảng $(-\infty;2) và (2;+\infty)$ $(-\infty;2) và (2;+\infty)$

b) $g(x) = \sqrt{9-x^{2}}$ $g(x) = \sqrt{9-x^{2}}$ là hàm số căn thức có tập xác định là [-3;3] nên hàm só g(x) liên tục trên đoạn [-3;3]

c) h(x) = cosx + tanx là hàm số lượng giác có tập xác định là $\mathbb{R} \ { \frac{\pi}{2} + k\pi }$ $\mathbb{R} \ { \frac{\pi}{2} + k\pi }$

Nên hàm số h(x) liên tục trên các khoảng $\mathbb{R} \ { \frac{\pi}{2} + k\pi }$ $\mathbb{R} \ { \frac{\pi}{2} + k\pi }$

Bài 4 trang 85

Cho hàm số f(x) = 2x -sinx , g(x) = $\sqrt{x-1}$ $\sqrt{x-1}$

Xét tính liên tục hàm số $y = f(x).g(x) và y = \frac{f(x)}{g(x)}$ $y = f(x).g(x) và y = \frac{f(x)}{g(x)}$

Gợi ý đáp án

Hàm số f(x) = 2x - sinx liên tục với mọi $x \in \mathbb{R}$ $x \in \mathbb{R}$

Hàm số $g(x) = \sqrt{x-1}$ $g(x) = \sqrt{x-1}$ liên tục trên khoảng $[1;+\infty)$ $[1;+\infty)$

Suy ra: hàm số $y=f(x).g(x)$ liên tục trên khoảng $[1;+\infty)$ $[1;+\infty)$

$g(x) \neq 0$ $g(x) \neq 0$ khi $x \neq 1$ $x \neq 1$

Suy ra hàm số $y=\frac{f(x)}{g(x)}$ $y=\frac{f(x)}{g(x)}$ liên tục trên khoảng $(1;+\infty)$ $(1;+\infty)$

Bài 5 trang 85

Một bãi đậu xe ô tô đưa ra giá C(x) (đồng) khi thời gian đậu xe là x (giờ) như sau:

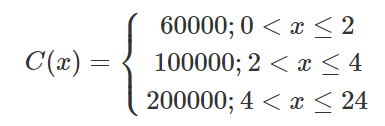
Xét tính liên tục của hàm số C(x).

Gợi ý đáp án

C(x) = 60000 khi $x \in (0;2)$ $x \in (0;2)$ nên hàm số C(x) liên tục trên (0;2)

C(x) = 100000 khi $x \in (2;4)$ $x \in (2;4)$ nên hàm số C(x) liên tục trên (2;4)

C(x) = 200000 khi $x \in (4;24)$ $x \in (4;24)$ nên hàm số C(x) liên tục trên (4;24)

Ta có:

$\lim_{x \to 2^{-}}C(x)= 60000$ $\lim_{x \to 2^{-}}C(x)= 60000$

$\lim_{x \to 2^{+}}C(x)= 100000$ $\lim_{x \to 2^{+}}C(x)= 100000$

Vậy không tồn tại $\lim_{x \to 2}$ $\lim_{x \to 2}$ hay hàm số C(x) không liên tục tại 2

$\lim_{x \to 4^{-}}C(x)= 100000$ $\lim_{x \to 4^{-}}C(x)= 100000$

$\lim_{x \to 4^{+}}C(x)= 200000$ $\lim_{x \to 4^{+}}C(x)= 200000$

Vậy không tồn tại $\lim_{x \to 4}$ $\lim_{x \to 4}$ hay hàm số C(x) không liên tục tại 4

Bài 6 trang 85

Lực hấp dẫn do Trái đất tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm của nó là:

$F(r)=\left\{\begin{matrix} \frac{GMr}{R^{3}}; 0 < r < R\\ \frac{GM}{r^{2}}; r\geq R\end{matrix}\right.$ $F(r)=\left\{\begin{matrix} \frac{GMr}{R^{3}}; 0 < r < R\\ \frac{GM}{r^{2}}; r\geq R\end{matrix}\right.$

Trong đó M là khối lương, R là bán kính của Trái đất, G là hằng số hấp dẫn. Hàm số F(r) có liên tục trên $(0;+\infty)$ $(0;+\infty)$ không?

Gợi ý đáp án

$\lim_{r \to R^{-}}F(r)=\lim_{r \to R^{-}}\frac{GMr}{R^{3}}=\frac{GMR}{R^{3}}=\frac{GM}{R^{2}}$ $\lim_{r \to R^{-}}F(r)=\lim_{r \to R^{-}}\frac{GMr}{R^{3}}=\frac{GMR}{R^{3}}=\frac{GM}{R^{2}}$

$\lim_{r \to R^{+}}F(r)=\lim_{r \to R^{+}}\frac{GM}{r^{2}}=\frac{GM}{R^{2}}$ $\lim_{r \to R^{+}}F(r)=\lim_{r \to R^{+}}\frac{GM}{r^{2}}=\frac{GM}{R^{2}}$

Suy ra: $\lim_{r \to R}F(r) = F(R)$ $\lim_{r \to R}F(r) = F(R)$. Hay hàm số F(r) liên tục tại $r_{0} = R$ $r_{0} = R$

$F(r)= \frac{GMr}{R^{3}} khi 0 < r < R$ $F(r)= \frac{GMr}{R^{3}} khi 0 < r < R$ nên hàm F(r) liên tục trên (0;R)

$F(r)= \frac{GM}{r^{3}}$ $F(r)= \frac{GM}{r^{3}}$ khi r > R nên hàm F(r) liên tục trên $(R;+\infty)$ $(R;+\infty)$

Vậy hàm số F(r) liên tục trên $(0;+\infty)$ $(0;+\infty)$