Toán 11 Bài tập cuối chương I Giải Toán 11 Chân trời sáng tạo trang 42, 43

Mục lục

Giải Toán 11 Bài tập cuối chương I là tài liệu vô cùng hữu ích giúp các em học sinh lớp 11 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 11 Chân trời sáng tạo tập 1 trang 42, 43.

Toán 11 Chân trời sáng tạo tập 1 trang 42, 43 được biên soạn đầy đủ, chi tiết trả lời các câu hỏi từ bài 1 đến 14 chương Hàm số lượng giác và phương trình lượng giác giúp các bạn có thêm nhiều nguồn ôn tập đối chiếu với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết giải Toán 11 tập 1 Bài tập cuối chương I Chân trời sáng tạo, mời các bạn cùng theo dõi tại đây.

Toán 11 Bài tập cuối chương I

Giải Toán lớp 11 Chân trời sáng tạo tập 1 trang 42, 43

Xem thêm

I. Giải Toán lớp 11 Chân trời sáng tạo tập 1 trang 42, 43

Bài 1 trang 42

Góc lượng giác nào tương ứng với chuyển động quay 3 $\frac{1}{5}$ $\frac{1}{5}$ vòng ngược chiều kim đồng hồ?

A. $\frac{16\pi }{5}$ $\frac{16 π}{5}$

B. ( $\frac{16}{5}$ $\frac{16}{5}$ )^o

C. 1152^o

D. 1152π

Gợi ý đáp án

Đáp án C

Bài 2 trang 42

Trong trường hợp nào dưới đây cosα = cos $\beta$ $β$ và sinα = −sin $\beta$ $β$

A. $\beta$ $β$ = −α

B. $\beta$ $β$ = π − α

C. $\beta$ $β$ = π + α

D. $\beta$ $β$ = $\frac{\pi }{2}$ $\frac{π}{2}$ + α

Gợi ý đáp án

Đáp án A

Bài 3 trang 42

Khẳng định nào sau đây là đúng?

A. Hàm số y = sinx là hàm số chẵn.

B. Hàm số y = cosx là hàm số chẵn

C. Hàm số y = tanx là hàm số chẵn

D. Hàm số y = cotx là hàm số chẵn

Gợi ý đáp án

Đáp án B

Bài 4 trang 42

Nghiệm âm lớn nhất của phương trình lượng giác $cos2x = cos\left ( x+\frac{\pi }{3} \right )$ $c o s 2 x = c o s (x + \frac{π}{3})$ là:

A. $-\frac{\pi }{9}$ $- \frac{π}{9}$

B. $-\frac{5\pi }{3}$ $- \frac{5 π}{3}$

C. $-\frac{7\pi }{9}$ $- \frac{7 π}{9}$

D. $-\frac{13\pi }{9}$ $- \frac{13 π}{9}$

Gợi ý đáp án

$cos2x = cos\left ( x+\frac{\pi }{3} \right )$ $c o s 2 x = c o s (x + \frac{π}{3})$

$\Leftrightarrow 2x = x + \frac{\pi }{3} + k2\pi , k\in \mathbb{Z} hoặc 2x = -x - \frac{\pi }{3} + k2\pi , k\in \mathbb{Z}$ $\Leftrightarrow 2 x = x + \frac{π}{3} + k 2 π, k \in Z h o ặ c 2 x = - x - \frac{π}{3} + k 2 π, k \in Z$

$\Leftrightarrow x = \frac{\pi }{3} + k2\pi , k\in \mathbb{Z} hoặc x =- \frac{\pi }{9} + k\frac{2\pi}{3} , k\in \mathbb{Z}$ $\Leftrightarrow x = \frac{π}{3} + k 2 π, k \in Z h o ặ c x = - \frac{π}{9} + k \frac{2 π}{3}, k \in Z$

Nghiệm âm lớn nhất của phương trình là $x =- \frac{\pi }{9}$ $x = - \frac{π}{9}$

Đáp án: A

Bài 5 trang 42

Số nghiệm của phương trình tanx = 3 trong khoảng $\left ( -\frac{\pi }{2}; \frac{7\pi }{3} \right )$ $(- \frac{π}{2}; \frac{7 π}{3})$ là

A. 1

B. 2

C. 3

D. 4

Gợi ý đáp án

$tanx = 3\Leftrightarrow x = 1,25 + k\pi , k\in \mathbb{Z}$ $t a n x = 3 \Leftrightarrow x = 1, 25 + k π, k \in Z$

Ta có: $-\frac{\pi}{2}< x<\frac{7\pi }{3}$ $- \frac{π}{2} < x < \frac{7 π}{3}$ . Suy ra: $-\frac{\pi}{2}<1,25 + k\pi<\frac{7\pi }{3}, k\in \mathbb{Z}$ $- \frac{π}{2} < 1, 25 + k π < \frac{7 π}{3}, k \in Z$

Hay $-0,9 < k < 1,9, k\in \mathbb{Z}$ $- 0, 9 < k < 1, 9, k \in Z$

Có 2 số nguyên k thoả mãn. Vậy phương trình tanx = 3 có 2 nghiệm

Đáp án: B

Bài 6 trang 42

Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức: h(t) = 29 + 3sin $\frac{\pi }{12}$ $\frac{π}{12}$ (t − 9) với h tính bằng độ C và t là thời gian trong ngày tính bằng giờ. Nhiệt độ thấp nhất trong ngày là bao nhiêu độ C và vào lúc mấy giờ?

A. 32^oC, lúc 15 giờ

B. 29^oC, lúc 9 giờ

C. 26^oC, lúc 3 giờ

D. 26^oC, lúc 0 giờ

Gợi ý đáp án

Đáp án C

Bài 7 trang 42

Một chiếc quạt trần năm cánh quay với tốc độ 45 vòng một phút. Chọn chiều quay của quạt là chiều thuận. Sau 3 giây, quạt quay được một góc có số đo bao nhiêu radian?

Gợi ý đáp án

Trong 3 giây, quạt quay được: 3. $\frac{45}{60}$ $\frac{45}{60}$ = $\frac{9}{4}$ $\frac{9}{4}$ (vòng)

Vậy quạt quay dược một góc: 2π . $\frac{9}{4}$ $\frac{9}{4}$ = $\frac{9\pi }{2}$ $\frac{9 π}{2}$ (rad)

Bài 8 trang 42

Cho $cos\alpha = \frac{1}{3} và -\frac{\pi }{2}<\alpha <0$ $c o s α = \frac{1}{3} v à - \frac{π}{2} < α < 0$ . Tính

a) $sin\alpha$ $s i n α$

b) $sin2\alpha$ $s i n 2 α$

c) $cos\left ( \alpha +\frac{\pi }{3} \right )$ $c o s (α + \frac{π}{3})$

Gợi ý đáp án

a) Do $-\frac{\pi }{2}<\alpha <0 nên sin\alpha < 0$ $- \frac{π}{2} < α < 0 n ê n s i n α < 0$

$sin\alpha = -\sqrt{1-cos^{2}\alpha } = \frac{-2\sqrt{2}}{3}$ $s i n α = - \sqrt{1 - c o s^{2} α} = \frac{- 2 \sqrt{2}}{3}$

b) $sin2\alpha =2sin\alpha .cos=2\frac{-2\sqrt{2}}{3}.\frac{1}{3} = \frac{-4\sqrt{2}}{9}$ $s i n 2 α = 2 s i n α . c o s = 2 \frac{- 2 \sqrt{2}}{3} . \frac{1}{3} = \frac{- 4 \sqrt{2}}{9}$

c) $cos\left ( \alpha +\frac{\pi }{3} \right ) = cos\alpha .cos\frac{\pi }{3}-sin\alpha .sin\frac{\pi }{3}$ $c o s (α + \frac{π}{3}) = c o s α . c o s \frac{π}{3} - s i n α . s i n \frac{π}{3}$

$cos\left ( \alpha +\frac{\pi }{3} \right ) = \frac{1}{3}.\frac{1}{2}-\frac{-2\sqrt{2}}{3} .\frac{\sqrt{3}}{2} = \frac{1+2\sqrt{6}}{6}$ $c o s (α + \frac{π}{3}) = \frac{1}{3} . \frac{1}{2} - \frac{- 2 \sqrt{2}}{3} . \frac{\sqrt{3}}{2} = \frac{1 + 2 \sqrt{6}}{6}$

Bài 9 trang 42

Chứng minh đẳng thức lượng giác:

a) $sin(\alpha +\beta ).sin(\alpha -\beta ) = sin^{2}\alpha -sin^{2}\beta$ $s i n (α + β) . s i n (α - β) = s i n^{2} α - s i n^{2} β$

b) $cos^{4}\alpha -cos^{4}\left ( \alpha -\frac{\pi }{2} \right ) = cos2\alpha$ $c o s^{4} α - c o s^{4} (α - \frac{π}{2}) = c o s 2 α$

Gợi ý đáp án

a) $sin(\alpha +\beta ).sin(\alpha -\beta )$ $s i n (α + β) . s i n (α - β)$

$= \frac{1}{2}.\left (cos2\beta -cos2\alpha \right )$ $= \frac{1}{2} . (c o s 2 β - c o s 2 α)$

$= \frac{1}{2}.(1-2sin^{2}\beta -1+2sin^{2}\alpha )$ $= \frac{1}{2} . (1 - 2 s i n^{2} β - 1 + 2 s i n^{2} α)$

$= sin^{2}\alpha -sin^{2}\beta$ $= s i n^{2} α - s i n^{2} β$

b) $cos^{4}\alpha -cos^{4}\left ( \alpha -\frac{\pi }{2} \right )$ $c o s^{4} α - c o s^{4} (α - \frac{π}{2})$

$= cos^{4}\alpha -sin^{4}\alpha$ $= c o s^{4} α - s i n^{4} α$

$= (cos^{2}\alpha +sin^{2}\alpha )(cos^{2}\alpha -sin^{2}\alpha )$ $= (c o s^{2} α + s i n^{2} α) (c o s^{2} α - s i n^{2} α)$

$= cos2\alpha$ $= c o s 2 α$

Bài 10 trang 42

Nghiệm dương nhỏ nhất của phương trình $sin\left ( x+\frac{\pi }{6} \right )-sin2x = 0$ $s i n (x + \frac{π}{6}) - s i n 2 x = 0$ là bao nhiêu?

Gợi ý đáp án

$sin\left ( x+\frac{\pi }{6} \right )-sin2x = 0$ $s i n (x + \frac{π}{6}) - s i n 2 x = 0$

$\Leftrightarrow sin\left ( x+\frac{\pi }{6} \right )=sin2x$ $\Leftrightarrow s i n (x + \frac{π}{6}) = s i n 2 x$

$\Leftrightarrow x+\frac{\pi }{6} = 2x + k2\pi, k\in \mathbb{Z} hoặc x+\frac{\pi }{6} = \pi -2x + k2\pi, k\in \mathbb{Z}$ $\Leftrightarrow x + \frac{π}{6} = 2 x + k 2 π, k \in Z h o ặ c x + \frac{π}{6} = π - 2 x + k 2 π, k \in Z$

$\Leftrightarrow x = -\frac{\pi }{6} -k2\pi ,k\in \mathbb{Z} hoặc x =\frac{5\pi }{18} + k.\frac{2\pi }{3}, k\in \mathbb{Z}$ $\Leftrightarrow x = - \frac{π}{6} - k 2 π, k \in Z h o ặ c x = \frac{5 π}{18} + k . \frac{2 π}{3}, k \in Z$

Vậy nghiệm dương nhỏ nhất của phương trình là: $\frac{5\pi }{18}$ $\frac{5 π}{18}$

Bài 11 trang 42

Giải các phương trình sau:

a) sin2x + cos3x = 0

b) $sinxcosx = \frac{\sqrt{2}}{4}$ $s i n x c o s x = \frac{\sqrt{2}}{4}$

c) sinx + sin2x = 0

Gợi ý đáp án

a) sin2x + cos3x = 0

$\Leftrightarrow cos\left ( 2x-\frac{\pi }{2} \right )+cos3x = 0$ $\Leftrightarrow c o s (2 x - \frac{π}{2}) + c o s 3 x = 0$

$\Leftrightarrow 2.cos\left ( \frac{5}{2}x-\frac{\pi }{4} \right ).cos\left ( \frac{1}{2}x + \frac{\pi }{4} \right )=0$ $\Leftrightarrow 2. c o s (\frac{5}{2} x - \frac{π}{4}) . c o s (\frac{1}{2} x + \frac{π}{4}) = 0$

$\Leftrightarrow cos\left ( \frac{5}{2}x-\frac{\pi }{4} \right ) = 0 hoặc cos\left ( \frac{1}{2}x + \frac{\pi }{4} \right ) = 0$ $\Leftrightarrow c o s (\frac{5}{2} x - \frac{π}{4}) = 0 h o ặ c c o s (\frac{1}{2} x + \frac{π}{4}) = 0$

$\Leftrightarrow \frac{5}{2}x-\frac{\pi }{4} = \frac{\pi }{2}+k\pi , k\in \mathbb{Z} hoặc \frac{1}{2}x + \frac{\pi }{4} = \frac{\pi }{2}+k\pi$ $\Leftrightarrow \frac{5}{2} x - \frac{π}{4} = \frac{π}{2} + k π, k \in Z h o ặ c \frac{1}{2} x + \frac{π}{4} = \frac{π}{2} + k π$

$\Leftrightarrow x = \frac{3\pi }{10}+k\frac{2\pi }{5}, k\in \mathbb{Z} hoặc x = \frac{\pi }{2} +k2\pi,k\in \mathbb{Z}$ $\Leftrightarrow x = \frac{3 π}{10} + k \frac{2 π}{5}, k \in Z h o ặ c x = \frac{π}{2} + k 2 π, k \in Z$

b) $\Leftrightarrow \frac{1}{2}cos2x = \frac{\sqrt{2}}{4}$ $\Leftrightarrow \frac{1}{2} c o s 2 x = \frac{\sqrt{2}}{4}$

$\Leftrightarrow cos2x = \frac{\sqrt{2}}{2}$ $\Leftrightarrow c o s 2 x = \frac{\sqrt{2}}{2}$

$\Leftrightarrow 2x = \frac{\pi }{4}+k2\pi , k\in \mathbb{Z} hoặc 2x = -\frac{\pi }{4}+k2\pi , k\in \mathbb{Z}$ $\Leftrightarrow 2 x = \frac{π}{4} + k 2 π, k \in Z h o ặ c 2 x = - \frac{π}{4} + k 2 π, k \in Z$

$\Leftrightarrow x = \frac{\pi }{8}+k\pi , k\in \mathbb{Z} hoặc x = -\frac{\pi }{8}+k\pi , k\in \mathbb{Z}$ $\Leftrightarrow x = \frac{π}{8} + k π, k \in Z h o ặ c x = - \frac{π}{8} + k π, k \in Z$

c) sinx + sin2x = 0

$\Leftrightarrow sinx = -sin2x$ $\Leftrightarrow s i n x = - s i n 2 x$

$\Leftrightarrow sinx = sin(-2x)$ $\Leftrightarrow s i n x = s i n (- 2 x)$

$\Leftrightarrow x = -2x + k2\pi ,k\in \mathbb{Z} hoặc x = \pi +2x + k2\pi , k\in \mathbb{Z}$ $\Leftrightarrow x = - 2 x + k 2 π, k \in Z h o ặ c x = π + 2 x + k 2 π, k \in Z$

$\Leftrightarrow x = k\frac{2\pi }{3},k\in \mathbb{Z} hoặc x = -\pi - k2\pi, k\in \mathbb{Z}$ $\Leftrightarrow x = k \frac{2 π}{3}, k \in Z h o ặ c x = - π - k 2 π, k \in Z$

Bài 12 trang 42

Độ sâu h (m) của mực nước ở một cảng biển vào thời điểm t (giờ) sau khi thuỷ triểu lên lần đầu tiên trong ngày được tính xấp xỉ bởi công thức h(t) = 0,8cos0,5t + 4.

a) Độ sâu của nước vào thời điểm t = 2 là bao nhiêu mét?

b) Một con tàu cần mực nước sâu tối thiểu 3,6 m để có thể di chuyển ra vào cảng an toàn. Dựa vào đồ thị của hàm số côsin, hãy cho biết trong vòng 12 tiếng đầu tiên sau khi thuỷ triểu lên lần đầu tiên, ở những thời điểm t nào tàu có thể hạ thuỷ. Làm tròn kết quả đến hàng phần trăm.

Gợi ý đáp án

a) Tại thời điểm t = 2. Ta có: h(t) = 0,8.cos(0,5.2) + 4 = 4,43 (m)

Dựa vào đồ thị hàm số cos:

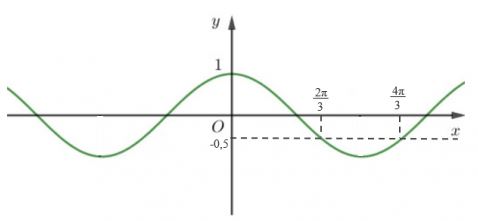
Những thời điểm tàu không thể hạ thuỷ là khi 0,8cos0,5t + 4 < 3,6 ⇔ cos0,5t < −0,5

⇔ 2π/3 < 0,5t < 4π/3

⇔ 4,19 < t <8,38

Vậy thời điểm tàu có thể hạ thuỷ là (0;4,19) ∪ (8,38;12)

Bài 13 trang 42

Cho vận tốc v (cm/s) của một con lắc đơn theo thời gian t (giây) được cho bởi công thức v = −3sin(1,5t + $\frac{\pi }{3}$ $\frac{π}{3}$ ).

Xác định các thời điểm t mà tại đó:

a) Vận tốc con lắc đạt giá trị lớn nhất

b) Vận tốc con lắc bằng 1,5 cm/s

Gợi ý đáp án

a) Vận tốc con lắc đạt giá trị lớn nhất khi $sin\left ( 1,5t +\frac{\pi }{3} \right )=-1$ $s i n (1, 5 t + \frac{π}{3}) = - 1$

$\Leftrightarrow 1,5t +\frac{\pi }{3} = \frac{3\pi}{2}+k2\pi, k\in \mathbb{Z}$ $\Leftrightarrow 1, 5 t + \frac{π}{3} = \frac{3 π}{2} + k 2 π, k \in Z$

$\Leftrightarrow t = \frac{7\pi}{9}+ \frac{4\pi}{3}k,k\in \mathbb{Z}$ $\Leftrightarrow t = \frac{7 π}{9} + \frac{4 π}{3} k, k \in Z$

b) Khi v = 1,5 Ta có:

$sin\left ( 1,5t +\frac{\pi }{3} \right )= \frac{-1}{2}$ $s i n (1, 5 t + \frac{π}{3}) = \frac{- 1}{2}$

$\Leftrightarrow 1,5t +\frac{\pi }{3} = \frac{7\pi}{6}+k2\pi, k\in \mathbb{Z} hoặc 1,5t +\frac{\pi }{3} = \frac{-\pi}{6}+k2\pi, k\in \mathbb{Z}$ $\Leftrightarrow 1, 5 t + \frac{π}{3} = \frac{7 π}{6} + k 2 π, k \in Z h o ặ c 1, 5 t + \frac{π}{3} = \frac{- π}{6} + k 2 π, k \in Z$

$\Leftrightarrow t = \frac{5\pi}{9}+ \frac{4\pi}{3}k,k\in \mathbb{Z} hoặc t = \frac{-\pi}{3}+ \frac{4\pi}{3}k,k\in \mathbb{Z}$ $\Leftrightarrow t = \frac{5 π}{9} + \frac{4 π}{3} k, k \in Z h o ặ c t = \frac{- π}{3} + \frac{4 π}{3} k, k \in Z$

II. Luyện tập Ôn tập chương 1

Chia sẻ bởi:

Trịnh Thị Thanh

Tải về

Bài trước

Bài 5: Phương trình lượng giác cơ bản

Bài sau

Bài 1: Dãy số

Liên kết tải về

Toán 11 Bài tập cuối chương I 338,4 KB Tải về

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!