Download.vn Học tập Lớp 6 Toán 6 KNTT

Toán 6 Bài tập cuối chương VI - Kết nối tri thức với cuộc sống Giải Toán lớp 6 trang 27 - Tập 2

Tải về Bình luận
  • 299
Mục lục

Giải Toán lớp 6 Bài tập cuối chương VI bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 6 Tập 2 Kết nối tri thức với cuộc sống trang 27.

Với lời giải chi tiết, trình bày khoa học, được biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 6, từ đó học tốt môn Toán lớp 6 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài tập cuối chương Chương VI: Phân số. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 6 Bài tập cuối chương VI sách Kết nối tri thức với cuộc sống

Giải Toán 6 Kết nối tri thức với cuộc sống trang 27 tập 2

Bài 6.44

Thay số thích hợp vào dấu “?”.

\frac{-10}{16}=\frac{?}{56}=\frac{-20}{?}=\frac{50}{?}

Hướng dẫn giải

Để viết lại các phân số có cùng mẫu dương ta có thể sử dụng 1 trong hai tính chất sau:

  • Tính chất 1: Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho.
  • Tính chất 2: Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho.

Gợi ý trả lời:

\frac{-10}{16}=\frac{-35}{56}=\frac{-20}{-32}=\frac{50}{80}

Bài 6.45

Tính một cách hợp lí:

a. A=\frac{-3}{14}+\frac{2}{13}+\frac{-25}{14}+\frac{-15}{13};

b. B=\frac{5}{3}.\frac{7}{25}+\frac{5}{3}.\frac{21}{25}-\frac{5}{3}.\frac{7}{25}.

Hướng dẫn giải

  • Thứ tự thực hiện phép tính: Nhân chia trước, cộng trừ sau
  • Tính chất giao hoán: a + b = b + a
  • Tính chất kết hợp: (a + b) + c = a + (b + c)
  • Tính chất phân phối của phép nhân đối với phép cộng: a . (b + c) = ab + ac
  • Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau.
  • Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia.

Gợi ý trả lời:

a. A=\frac{-3}{14}+\frac{2}{13}+\frac{-25}{14}+\frac{-15}{13}

A=(\frac{-3}{14}+\frac{-25}{14})+(\frac{2}{13}+\frac{-15}{13})

A=-2+-1=-3

b. B=\frac{5}{3}.\frac{7}{25}+\frac{5}{3}.\frac{21}{25}-\frac{5}{3}.\frac{7}{25}

B=\frac{5}{3}.(\frac{7}{25}+\frac{21}{25}-\frac{7}{25})

B=\frac{5}{3}.\frac{21}{25}=\frac{7}{5}.

Bài 6.46

Mẹ mua cho Mai một hộp sữa tươi loại 1000 ml. Ngày đầu Mai uống \frac{1}{5} hộp; ngày tiếp theo Mai uống tiếp \frac{1}{4}. Hỏi:

a. Sau hai ngày hộp sữa tươi còn lại bao nhiêu phần?

b. Tính lượng sữa tươi còn lại sau hai ngày.

Hướng dẫn giải

- Muốn tìm \frac{m}{n} của một số a cho trước ta tính a.\frac{m}{n};\left( {m \in \mathbb{N},n \in {\mathbb{N}^*}} \right)

- Muốn tìm \frac{m}{n} của một số b cho trước ta tính

- Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau.

- Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia.

Gợi ý trả lời:

a. Sau hai ngày hộp sữa tươi còn lại số phần là: 1-\frac{1}{5}-\frac{1}{4}=\frac{11}{20} (phần)

b. Lượng sữa tươi còn lại sau hai ngày là: 1000.\frac{11}{20}=550(ml)

Bài 6.47

Một bác nông dân thu hoạch và mang cà chua ra chợ bán. Bác đã bán được 20 kg, tức là \frac{2}{5} số cà chua. Hỏi bác nông dân đã mang bao nhiêu kilogam cà chua ra chợ bán?

Hướng dẫn giải:

- Muốn tìm \frac{m}{n} của một số a cho trước ta tính a.\frac{m}{n};\left( {m \in \mathbb{N},n \in {\mathbb{N}^*}} \right)

- Muốn tìm \frac{m}{n} của một số b cho trước ta tính b:\frac{m}{n};\left( {m,n \in {\mathbb{N}^*}} \right)

- Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau.

- Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia.

Gợi ý trả lời:

Bác nông dân đã mang số kilogam cà chua ra chợ bán là:

20:\frac{2}{5}=50(kg)

Bài 6.48

Con người ngủ khoảng 8 giờ mỗi ngày. Nếu trung bình một năm có 365\frac{1}{4} ngày, hãy cho biết số ngày ngủ trung bình mỗi năm của con người?

Hướng dẫn giải

1 ngày = 24 giờ

Cách đổi hỗn số ra phân số: a\frac{b}{c} = \frac{{a.c + b}}{c}

Gợi ý trả lời:

Đổi 365\frac{1}{4} ngày=\frac{1461}{4} ngày

Số ngày ngủ trung bình mỗi năm của con người là:

\frac{1461}{4} :8=\frac{1461}{32} (ngày)

Bài 6.49

Các phân số sau được sắp xếp theo một quy luật, hãy quy đồng mẫu các phân số để tìm quy luật, rồi viết hai phân số liên tiếp.

\frac{1}{8},\frac{1}{20},\frac{-1}{40},\frac{-1}{10},…,…

Hướng dẫn giải

Muốn so sánh các phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các từ với nhau: Phân số nào có tử lớn hơn thì phân số đó lớn hơn.

Để viết lại các phân số có cùng mẫu dương ta có thể sử dụng 1 trong hai tính chất sau:

  • Tính chất 1: Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho.
  • Tính chất 2: Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho.

Gợi ý trả lời:

Quy đồng ta được: \frac{5}{40},\frac{2}{40},\frac{-1}{40},\frac{-4}{40}

=> Rút ra quy luật số sau kém số trước 3 đơn vị nên ta điền tiếp được là:

\frac{5}{40},\frac{2}{40},\frac{-1}{40},\frac{-4}{40},\frac{-7}{40},\frac{-10}{40}.

Bài 6.50

Trong hình dưới đây, cân đang ở vị trí thăng bằng.

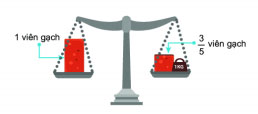
Bài 6.50

Đố em biết một viên gạch cân nặng bao nhiêu kg?

Hướng dẫn giải

Muốn so sánh các phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các từ với nhau: Phân số nào có tử lớn hơn thì phân số đó lớn hơn.

Gợi ý trả lời:

Vì cân thăng bằng, nên phần nặng 1 kg là:

1 – \frac{3}{5} = \frac{2}{5}(viên gạch)

Khối lượng của viên gạch là:

1 : \frac{2}{5} = \frac{5}{2}(kg)

Vậy: viên gạch nặng \frac{5}{2} kg

Lý thuyết Chương VI: Phân số

1. Hai phân số bằng nhau

Hai phân số \frac{a}{b} và \frac{c}{d} được gọi là bằng nhau, viết là \frac{a}{b} = \frac{c}{d}, nếu a.d = b.c.

Chú ý: Điều kiện a.d = b.c gọi là điều kiện bằng nhau của hai phân số \frac{a}{b} và \frac{c}{d}.

2.

2. So sánh hai phân số

a) So sánh hai phân số cùng mẫu

Trong hai phân số cùng một mẫu dương, phân số nào có tử lớn hơn thì phân số đó lớn hơn.

b) So sánh hai phân số không cùng mẫu

Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử số với nhau: phân số nào có tử số lớn hơn thì phân số đó lớn hơn.

3. Phép cộng hai phân số

a) Cộng hai phân số cùng mẫu:

Muốn cộng hai phân số cùng mẫu, ta cộng các tử và giữ nguyên mẫu.

\dfrac{a}{m} + \dfrac{b}{m} = \dfrac{{a + b}}{m} (m \ne 0)

Ví dụ:

\dfrac{8}{5} + \dfrac{7}{5} = \dfrac{{8 + 7}}{5} = \dfrac{{15}}{5} = 3

b) Cộng hai phân số khác mẫu:

Muốn cộng hai phân số khác mẫu, ta viết chúng dưới dạng hai phân số cùng mẫu rồi cộng các tử với nhau và giữ nguyên mẫu chung.

Ví dụ:

\dfrac{3}{2} + \dfrac{{ - 3}}{5} = \dfrac{{15}}{{10}} + \dfrac{{ - 6}}{{10}} = \dfrac{{15 + \left( { - 6} \right)}}{{10}} = \dfrac{9}{{10}}

4. Phép trừ hai phân số

- Muốn trừ hai phân số cùng mẫu ta lấy tử của phân số thứ nhất trừ đi tử của phân số thứ hai và giữ nguyên mẫu.

\dfrac{a}{m} - \dfrac{b}{m} = \dfrac{{a - b}}{m}

- Muốn trừ hai phân số khác mẫu, ta quy đồng hai phân số, rồi trừ hai phân số đó.

Ví dụ:

a) \dfrac{2}{7} - \dfrac{5}{7} = \dfrac{{2 - 5}}{7} = \dfrac{{ - 3}}{7}

b) \dfrac{1}{6} - \dfrac{1}{2} = \dfrac{1}{6} + \left( { - \dfrac{1}{2}} \right) = \dfrac{1}{6} + \left( {\dfrac{{ - 3}}{6}} \right) = \dfrac{{1 + \left( { - 3} \right)}}{6} = \dfrac{{ - 2}}{6} = \dfrac{{ - 1}}{3}

Nhận xét: Muốn trừ một phân số cho một phân số, ta có thể cộng số bị trừ với số đối của số trừ.

5. Phép nhân hai phân số

+ Muốn nhân hai phân số, ta nhân các tử số với nhau và nhân các mẫu với nhau.

\dfrac{a}{b}.\dfrac{c}{d} = \dfrac{{a.c}}{{b.d}}

+ Muốn nhân một số nguyên với một phân số (hoặc một phân số với một số nguyên), ta nhân số nguyên với tử của phân số và giữ nguyên mẫu: a.\dfrac{b}{c} = \dfrac{{a.b}}{c}

Ví dụ:

a) \dfrac{{ - 1}}{4}.\dfrac{1}{5} = \dfrac{{\left( { - 1} \right).1}}{{4.5}} = \dfrac{{ - 1}}{{20}}

b) 2.\dfrac{4}{5} = \dfrac{{2.4}}{5} = \dfrac{8}{5}

6. Phép chia hai phân số

Muốn chia một phân số hay một số nguyên cho một phân số, ta nhân số bị chia với số nghịch đảo của số chia.

\dfrac{a}{b}:\dfrac{c}{d} = \dfrac{a}{b}.\dfrac{d}{c} = \dfrac{{a.d}}{{b.c}}

a:\dfrac{c}{d} = a.\dfrac{d}{c} = \dfrac{{a.d}}{c}\left( {c \ne 0} \right)

Ví dụ: \dfrac{{ - 1}}{6}:\dfrac{3}{{13}} = \dfrac{{ - 1}}{6}.\dfrac{{13}}{3} = \dfrac{{\left( { - 1} \right).13}}{{6.3}} = \dfrac{{ - 13}}{{18}}

Chia sẻ bởi: 👨 Hồng Linh
299
  • Lượt tải: 178
  • Lượt xem: 113.282
  • Dung lượng: 280,2 KB
Tìm thêm: Toán lớp 6 Kết nối tri thức với cuộc sống Kết nối tri thức với cuộc sống Lớp 6
1 Bình luận
Sắp xếp theo
Xóa Đăng nhập để Gửi
  • Bao Hoang
    Bao Hoang

    im, yes of no, is for time 😅🤣🤣

    Thích Phản hồi 09/03/22

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần

    Toán 6: Kết nối tri thức với Cuộc sống