Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn (không bao gồm tài liệu cao cấp) và trải nghiệm website không quảng cáo
Tìm hiểu thêm »Giải bài tập SGK Toán 9 trang 89, 90 giúp các em học sinh lớp 9 xem gợi ý giải các bài tập của Bài 7: Tứ giác nội tiếp thuộc Hình học 9 Chương 3. Qua đó các em sẽ nhanh chóng hoàn thiện toàn bộ bài tập của bài 7 Chương III Hình học 9 tập 2. Chúc các em học tốt.
1. Khái niệm tứ giác nội tiếp
Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp)
 2. Định lý.
2. Định lý.
+ Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180°.
+ Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180° thì tứ giác đó nội tiếp được đường tròn
3. Dấu hiệu nhận biết tứ giác nội tiếp
+ Tứ giác có tổng hai góc đối bằng 180°.
+ Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
+ Tứ giác có bốn đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác đó.
+ Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc α.
+ Chú ý: Để chứng minh một tứ giác là tứ giác nội tiếp ta có thể chứng minh tứ giác đó là một trong các hình sau: Hình chữ nhật, hình vuông, hình thang cân.
Biết ABCD là tứ giác nội tiếp. Hãy điền vào ô trống trong bẳng sau (nếu có thể).
| Trường hợp | 1 | 2 | 3 | 4 | 5 | 6 |
| Góc A | 800 | 600 | 950 | |||
| Góc B | 700 | 400 | 650 | |||
| Góc C | 740 | |||||
| Góc D | 980 |
Theo đề bài ta có ABCD là tứ giác nội tiếp  \(\Rightarrow \left\{ \begin{array}{l}\widehat A + \widehat C = {180^0}\\\widehat B + \widehat D = {180^0}\end{array} \right..\)
\(\Rightarrow \left\{ \begin{array}{l}\widehat A + \widehat C = {180^0}\\\widehat B + \widehat D = {180^0}\end{array} \right..\)
- Trường hợp 1:
Ta có: ![]() \(\widehat A + \widehat C = {180^0}\)
\(\widehat A + \widehat C = {180^0}\)
![]() \(\Rightarrow \widehat C = {180^0}-\widehat A= {180^0} - {80^0} = {100^0}.\)
\(\Rightarrow \widehat C = {180^0}-\widehat A= {180^0} - {80^0} = {100^0}.\)
![]() \(\widehat B + \widehat D = {180^0}\)
\(\widehat B + \widehat D = {180^0}\)
![]() \(\Rightarrow \widehat D = {180^0} - \widehat B = {180^0} - {70^0} = {110^0}.\)
\(\Rightarrow \widehat D = {180^0} - \widehat B = {180^0} - {70^0} = {110^0}.\)
Vậy các góc còn lại là: ![]() \(\widehat{C}= 100^0, \widehat{D} = 110^0.\)
\(\widehat{C}= 100^0, \widehat{D} = 110^0.\)
- Trường hợp 2:
 \(\begin{array}{l} Ta \, \, có: \, \,
\widehat A + \widehat C = {180^0} \\\Rightarrow \widehat A = {180^0} - \widehat C = {180^0} - {105^0} = {75^0}.\\
\widehat B + \widehat D = {180^0}\\ \Rightarrow \widehat B = {180^0} - \widehat D = {180^0} - {75^0} = {105^0}.
\end{array}\)
\(\begin{array}{l} Ta \, \, có: \, \,
\widehat A + \widehat C = {180^0} \\\Rightarrow \widehat A = {180^0} - \widehat C = {180^0} - {105^0} = {75^0}.\\
\widehat B + \widehat D = {180^0}\\ \Rightarrow \widehat B = {180^0} - \widehat D = {180^0} - {75^0} = {105^0}.
\end{array}\)
- Trường hợp 3:
Ta có: ![]() \(\widehat A + \widehat C = {180^0}\)
\(\widehat A + \widehat C = {180^0}\)
![]() \(\Rightarrow \widehat C = {180^0}-\widehat A= {180^0} - {60^0} = {120^0}.\)
\(\Rightarrow \widehat C = {180^0}-\widehat A= {180^0} - {60^0} = {120^0}.\)
Có ![]() \(\widehat B + \widehat D = {180^0}.\)
\(\widehat B + \widehat D = {180^0}.\)
Ta có thể chọn ![]() \(\widehat B =70^0 \Rightarrow \widehat D = {180^0}-70^0=110^0.\)
\(\widehat B =70^0 \Rightarrow \widehat D = {180^0}-70^0=110^0.\)
- Trường hợp 4:![]() \(\widehat{D}=180^0-\widehat{B}=180^0 – 40^0= 140^0.\)
\(\widehat{D}=180^0-\widehat{B}=180^0 – 40^0= 140^0.\)
Còn lại ![]() \(\widehat{A}+ \widehat{C}= 180^0\). Chẳng hạn chọn
\(\widehat{A}+ \widehat{C}= 180^0\). Chẳng hạn chọn ![]() \(\widehat{A}=100^0,\,\widehat{C}=80^0.\)
\(\widehat{A}=100^0,\,\widehat{C}=80^0.\)
- Trường hợp 5: ![]() \(\widehat{A}=180^0-\widehat{C}=180^0–74^0=106^0.\)
\(\widehat{A}=180^0-\widehat{C}=180^0–74^0=106^0.\)
![]() \(\widehat{B}= 180^0-\widehat{D}=180^0–65^0=115^0.\)
\(\widehat{B}= 180^0-\widehat{D}=180^0–65^0=115^0.\)
- Trường hợp 6:![]() \(\widehat{C}=180^0-\widehat{A}=180^0–95^0=85^0.\)
\(\widehat{C}=180^0-\widehat{A}=180^0–95^0=85^0.\)
![]() \(\widehat{B}=180^0-\widehat{D}=180^0– 98^0=82^0.\)
\(\widehat{B}=180^0-\widehat{D}=180^0– 98^0=82^0.\)
Vậy điền vào ô trống ta được bảng sau:
| Trường hợp | 1 | 2 | 3 | 4 | 5 | 6 |
| Góc A | 800 | 750 | 600 | 1000 | 1060 | 950 |
| Góc B | 700 | 1050 | 700 | 400 | 650 | 820 |
| Góc C | 1000 | 1050 | 1200 | 800 | 740 | 850 |
| Góc D | 1100 | 750 | 1100 | 1400 | 1150 | 980 |
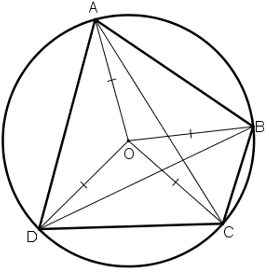
Tứ giác ABCD có góc ABC + góc ADC = 180o. Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm.
Vẽ hình minh họa
Tứ giác ABCD có ![]() \(\widehat{ABC}+ \widehat{ADC}= 180^0\) mà hai góc
\(\widehat{ABC}+ \widehat{ADC}= 180^0\) mà hai góc ![]() \(\widehat{ABC}\) và
\(\widehat{ABC}\) và ![]() \(\widehat{ADC}\) là hai góc ở vị trí đối nhau nên tứ giác ABCD là tứ giác nội tiếp.
\(\widehat{ADC}\) là hai góc ở vị trí đối nhau nên tứ giác ABCD là tứ giác nội tiếp.
Gọi O là tâm đường tròn ngoại tiếp tứ giác ABCD, khi đó OA=OB=OC=OD (cùng bằng bán kính của đường tròn (O) )
+ Vì OA = OB nên O thuộc đường trung trực của đoạn AB
+ Vì OA = OC nên O thuộc đường trung trực của đoạn AC
+ Vì OD = OB nên O thuộc đường trung trực của đoạn BD
Do đó các đường trung trực của AB, BD, AB cùng đi qua tâm O của đường tròn ngoại tiếp tứ giác ABCD.
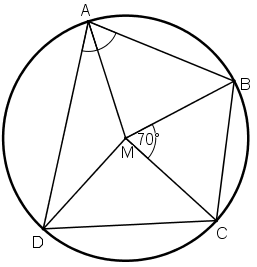
Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết ![]() \(\widehat {DAB}= 80^0, \widehat {DAM}= 30^0, \widehat {BMC}= 70^0.\)
\(\widehat {DAB}= 80^0, \widehat {DAM}= 30^0, \widehat {BMC}= 70^0.\)
Hãy tính số đo các góc ![]() \(\widehat {MAB}, \widehat {BCM}, \widehat {AMB}, \widehat {DMC}, \widehat {AMD}, \widehat {MCD}\) và
\(\widehat {MAB}, \widehat {BCM}, \widehat {AMB}, \widehat {DMC}, \widehat {AMD}, \widehat {MCD}\) và ![]() \(\widehat {BCD}.\)
\(\widehat {BCD}.\)
Vẽ hình minh họa
Ta có: ![]() \(\widehat {MAB} = \widehat {DAB} - \widehat {DAM} = {80^0} - {30^0} = {50^0}\)(1)
\(\widehat {MAB} = \widehat {DAB} - \widehat {DAM} = {80^0} - {30^0} = {50^0}\)(1)
+) ∆MBC là tam giác cân cân tại M (MB= MC) nên ![]() \(\displaystyle \widehat {BCM} = {{{{180}^0} - {{70}^0}} \over 2} = {55^0} (2)\)
\(\displaystyle \widehat {BCM} = {{{{180}^0} - {{70}^0}} \over 2} = {55^0} (2)\)
+) ∆MAB là tam giác cân tại M (MA=MB) nên ![]() \(\widehat {MAB} =\widehat {ABM} = {50^0}\) (theo (1)
\(\widehat {MAB} =\widehat {ABM} = {50^0}\) (theo (1)
Vậy ![]() \(\widehat {AMB} = {180^0} - {2.50^0} = {80^0}.\)
\(\widehat {AMB} = {180^0} - {2.50^0} = {80^0}.\)
Ta có: \(\widehat {BAD}=\dfrac{sđ\overparen{BCD}}{2}\) (số đo góc nội tiếp bằng nửa số đo của cung bị chắn).
\(\widehat {BAD}=\dfrac{sđ\overparen{BCD}}{2}\) (số đo góc nội tiếp bằng nửa số đo của cung bị chắn).
![]() \(\Rightarrow sđ\overparen{BCD}=2.\widehat {BAD} = {2.80^0} = {160^0}.\)
\(\Rightarrow sđ\overparen{BCD}=2.\widehat {BAD} = {2.80^0} = {160^0}.\)
Mà ![]() \(sđ\overparen{BC}= \widehat {BMC} = {70^0}\) (số đo góc ở tâm bằng số đo cung bị chắn).
\(sđ\overparen{BC}= \widehat {BMC} = {70^0}\) (số đo góc ở tâm bằng số đo cung bị chắn).
Vậy ![]() \(sđ\overparen{DC}={160^0} - {70^0} = {90^0}\) (vì C nằm trên cung nhỏ cung BD).
\(sđ\overparen{DC}={160^0} - {70^0} = {90^0}\) (vì C nằm trên cung nhỏ cung BD).
Suy ra ![]() \(\widehat {DMC} = {90^0}.\) (4)
\(\widehat {DMC} = {90^0}.\) (4)
Ta có: ∆MAD là tam giác cân cân tại M (MA= MD).
Suy ra ![]() \(\widehat {AMD} = {180^0} - {2.30^0}=120^0\) (5)
\(\widehat {AMD} = {180^0} - {2.30^0}=120^0\) (5)
Có ∆MCD là tam giác vuông cân tại M (MC= MD) và ![]() \(\widehat {DMC} = {90^0}\)
\(\widehat {DMC} = {90^0}\)
Suy ra ![]() \(\widehat {MCD} = \widehat {MDC} = {45^0}\). (6)
\(\widehat {MCD} = \widehat {MDC} = {45^0}\). (6)
Theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD ta có: ![]() \(\widehat {BCD} =\widehat{BCM}+\widehat{MCD} ={100^0}.\)
\(\widehat {BCD} =\widehat{BCM}+\widehat{MCD} ={100^0}.\)
Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD.
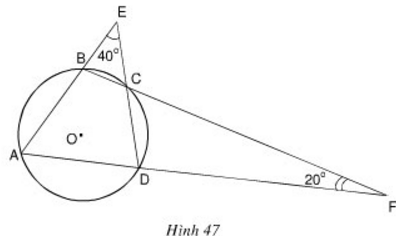
Ta có ![]() \(\widehat{BCE} = \widehat{DCF}\) (hai góc đối đỉnh)
\(\widehat{BCE} = \widehat{DCF}\) (hai góc đối đỉnh)
Đặt ![]() \(x = \widehat{BCE} = \widehat{DCF}\). Theo tính chất góc ngoài tam giác, ta có:
\(x = \widehat{BCE} = \widehat{DCF}\). Theo tính chất góc ngoài tam giác, ta có:
![]() \(\widehat{ABC}= x+40^0\) (góc ngoài của
\(\widehat{ABC}= x+40^0\) (góc ngoài của ![]() \(\Delta BCE\).) (1)
\(\Delta BCE\).) (1)
![]() \(\widehat{ADC}=x +20^0\) (góc ngoài của
\(\widehat{ADC}=x +20^0\) (góc ngoài của ![]() \(\Delta DCF\).) (2)
\(\Delta DCF\).) (2)
Lại có ![]() \(\widehat{ABC} +\widehat{ADC}=180^0\). (hai góc đối diện tứ giác nội tiếp). (3)
\(\widehat{ABC} +\widehat{ADC}=180^0\). (hai góc đối diện tứ giác nội tiếp). (3)
Từ (1), (2), (3) suy ra![]() \(: 180^0 =2x + 60^0 \Rightarrow x = 60^0.\)
\(: 180^0 =2x + 60^0 \Rightarrow x = 60^0.\)
Hay ![]() \(\widehat{BCE} = \widehat{DCF}=60^0.\)
\(\widehat{BCE} = \widehat{DCF}=60^0.\)
Từ (1), ta có:![]() \(\widehat{ABC}=60^0 +40^0 =100^0.\)
\(\widehat{ABC}=60^0 +40^0 =100^0.\)
Từ (2), ta có: ![]() \(\widehat{ADC} = 60^0+20^0 = 80^0.\)
\(\widehat{ADC} = 60^0+20^0 = 80^0.\)
![]() \(\widehat{BCD}= 180^0 – \widehat{BCE}\) (hai góc kề bù)
\(\widehat{BCD}= 180^0 – \widehat{BCE}\) (hai góc kề bù)
![]() \(\Rightarrow\widehat{BCD} = 120^0\)
\(\Rightarrow\widehat{BCD} = 120^0\)
![]() \(\widehat{BAD} = 180^0 - \widehat{BCD}\) (hai góc đối diện của tứ giác nội tiếp)
\(\widehat{BAD} = 180^0 - \widehat{BCD}\) (hai góc đối diện của tứ giác nội tiếp)
![]() \(\Rightarrow \widehat{BAD}= 180^0– 120^0= 60^0.\)
\(\Rightarrow \widehat{BAD}= 180^0– 120^0= 60^0.\)
Trong các hình sau, hình nào nội tiếp được trong một đường tròn:
Hình bình hành, hình chữ nhật, hình vuông, hình thang, hình thang vuông, hình thang cân? Vì sao?
* Hình bình hành nói chung không nội tiếp được đường tròn vì tổng hai góc đối diện không bằng ![]() \(180^0.\)
\(180^0.\)
* Trường hợp riêng của hình bình hành là hình chữ nhật (hay hình vuông) thì nội tiếp đường tròn vì tổng hai góc đối diện là ![]() \(90^0 + 90^0= 180^0.\)
\(90^0 + 90^0= 180^0.\)
* Hình thang nói chung và hình thang vuông không nội tiếp được đường tròn.
* Hình thang cân ABCD (BC= AD) có hai góc ở mỗi đáy bằng nhau:![]() \(\widehat{A}= \widehat{B}, \widehat{C} =\widehat{D}\)
\(\widehat{A}= \widehat{B}, \widehat{C} =\widehat{D}\)
Vì AD // CD nên ![]() \(\widehat{A} +\widehat{D} = 180^0\)(hai góc trong cùng phía), suy ra
\(\widehat{A} +\widehat{D} = 180^0\)(hai góc trong cùng phía), suy ra ![]() \(\widehat{A} +\widehat{C} =180^0.\)
\(\widehat{A} +\widehat{C} =180^0.\)
Vậy hình thang cân luôn có tổng hai góc đối diện bằng ![]() \(180^0\) nên là tứ giác nội tiếp.
\(180^0\) nên là tứ giác nội tiếp.
Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho DB = DC và ![]() \(\widehat{DCB}=\dfrac{1}{2}\widehat{ACB}.\)
\(\widehat{DCB}=\dfrac{1}{2}\widehat{ACB}.\)
a) Chứng minh ABDC là tứ giác nội tiếp.
b) Xác định tâm của đường tròn đi qua bốn điểm A, B, D,C.
Vẽ hình
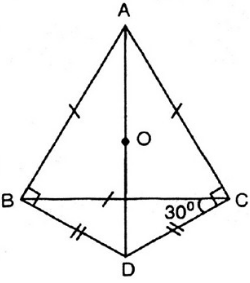
a) Theo giả thiết tam giác ABC đều nên ![]() \(\widehat{ACB}=60^0\)
\(\widehat{ACB}=60^0\)
Suy ra ![]() \(\widehat{DCB}=\dfrac{1}{2}\widehat{ACB} = \dfrac{1}{2} .60^0= 30^0.\)
\(\widehat{DCB}=\dfrac{1}{2}\widehat{ACB} = \dfrac{1}{2} .60^0= 30^0.\)
\widehat{ACD}=\widehat{ACB} +\widehat{BCD} (tia CB nằm giữa hai tia CA, CD)
![]() \(\Rightarrow\widehat{ACD}=60^0+ 30^0=90^0\) (1)
\(\Rightarrow\widehat{ACD}=60^0+ 30^0=90^0\) (1)
Do DB = CD nên ∆BDC cân tại D ![]() \(\Rightarrow \widehat{DBC} = \widehat{DCB} = 30^0\)
\(\Rightarrow \widehat{DBC} = \widehat{DCB} = 30^0\)
Từ đó ![]() \(\widehat{ABD}= 30^0+60^0=90^0\) (2)
\(\widehat{ABD}= 30^0+60^0=90^0\) (2)
Từ (1) và (2) có ![]() \(\widehat{ACD}+ \widehat{ABD}=180^0\) nên tứ giác ABDC là tứ giác nội tiếp.
\(\widehat{ACD}+ \widehat{ABD}=180^0\) nên tứ giác ABDC là tứ giác nội tiếp.
b) Vì ![]() \(\widehat{ABD} = 90^0\) nên AD là đường kính của đường tròn ngoại tiếp tứ giác ABDC, do đó tâm đường tròn ngoại tiếp tứ giác ABDC là trung điểm AD.
\(\widehat{ABD} = 90^0\) nên AD là đường kính của đường tròn ngoại tiếp tứ giác ABDC, do đó tâm đường tròn ngoại tiếp tứ giác ABDC là trung điểm AD.
Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, C cắt đường thẳng CD tại P khác C. Chứng minh AP = AD.
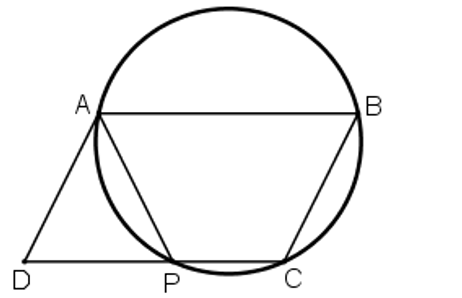
Do tứ giác ABCP nội tiếp nên ta có:
![]() \(\widehat{BAP} + \widehat{BCP} = 180^0.\)(1)
\(\widehat{BAP} + \widehat{BCP} = 180^0.\)(1)
Ta lại có: ![]() \(\widehat{ABC}+ \widehat{BCP}= 180^0\)(hai góc trong cùng phía do CD//AB). (2)
\(\widehat{ABC}+ \widehat{BCP}= 180^0\)(hai góc trong cùng phía do CD//AB). (2)
Từ (1) và (2) suy ra: ![]() \(\widehat{BAP}= \widehat{ABC}.\)
\(\widehat{BAP}= \widehat{ABC}.\)
Vậy ABCP là hình thang cân, suy ra AP = BC. (3)
Mà BC = AD (hai cạnh đối của hình bình hành) (4)
Từ (3) và (4) suy ra AP = AD (đpcm).
Xem hình 48. Chứng minh QR // ST.
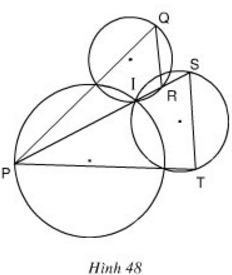
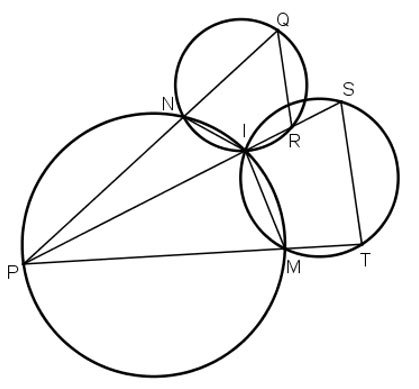
+) Ta có tứ giác ISTM nội tiếp đường tròn nên:
![]() \(\widehat{S_{1}}+ \widehat{M_1}=180^0\)
\(\widehat{S_{1}}+ \widehat{M_1}=180^0\)
Mà ![]() \(\widehat{M_{1}}+ \widehat{M_{3}}= 180^0\) (kề bù)
\(\widehat{M_{1}}+ \widehat{M_{3}}= 180^0\) (kề bù)
nên suy ra ![]() \(\widehat{S_{1}}= \widehat{M_{3}}\)(1)
\(\widehat{S_{1}}= \widehat{M_{3}}\)(1)
+) Ta có tứ giác IMPN nội tiếp đường tròn nên:
![]() \(\widehat{M_{3}}+ \widehat{PNI}=180^0\)
\(\widehat{M_{3}}+ \widehat{PNI}=180^0\)
Mà ![]() \(\widehat{N_{4}}+ \widehat{PNI}= 180^0\)(kề bù)
\(\widehat{N_{4}}+ \widehat{PNI}= 180^0\)(kề bù)
nên suy ra ![]() \(\widehat{M_{3}}= \widehat{N_{4}}\) (2)
\(\widehat{M_{3}}= \widehat{N_{4}}\) (2)
+) Ta có tứ giác INQS nội tiếp đường tròn nên:
![]() \(\widehat{N_{4}}+ \widehat{IRQ}=180^0\)
\(\widehat{N_{4}}+ \widehat{IRQ}=180^0\)
Mà (kề bù)
nên suy ra ![]() \(\widehat{N_{4}}= \widehat{R_{2}}\) (3)
\(\widehat{N_{4}}= \widehat{R_{2}}\) (3)
Từ (1), (2), (3) suy ra ![]() \(\widehat{S_{1}}= \widehat{R_{2}}\) (hai góc ở vị trí so le trong).
\(\widehat{S_{1}}= \widehat{R_{2}}\) (hai góc ở vị trí so le trong).
Do đó QR // ST.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: