Toán 9 Luyện tập chung trang 79 Giải SGK Toán 9 Hình học Tập 1 (trang 83, 84)

Mục lục

Giải Toán lớp 9 Luyện tập chung bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 9 Kết nối tri thức với cuộc sống tập 1 trang 79, 80.

Lời giải Toán 9 KNTT trang 79, 80 trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 9, từ đó học tốt môn Toán lớp 9 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Luyện tập chung Chương IV: Hệ thức lượng trong tam giác vuông. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Toán 9 Luyện tập chung Kết nối tri thức

Giải Toán 9 Kết nối tri thức Tập 1 trang 80

Giải Toán 9 Kết nối tri thức Tập 1 trang 80

Bài 4.14

Một cuốn sách khổ 17 × 24 cm, tức là chiều rộng 17 cm, chiều dài 24 cm. Gọi α là góc giữa đường chéo và cạnh 17 cm. Tính sinα, cosα (làm tròn đến chữ số thập phân thứ hai) và tính số đo α (làm tròn đến độ).

Lời giải:

Xét cuốn sách có dạng là hình chữ nhật chiều dài AB = CD = 24 cm; chiều rộng AC = BD = 17 cm.

Tam giác ACD vuông tại C có $A{D^2} = A{C^2} + C{D^2}$ $A D^{2} = A C^{2} + C D^{2}$ (định lý Pythagore)

Thay số ta có: $A{D^2} = {17^2} + {24^2} = 865$ $A D^{2} = 17^{2} + 24^{2} = 865$ hay $AD = \sqrt {865}$ $A D = \sqrt{865}$ cm (vì AD > 0)

$\sin \alpha = \frac{{CD}}{{AD}} = \frac{{24}}{{\sqrt {865} }} \approx 0,82;\cos \alpha = \frac{{AC}}{{AD}} = \frac{{17}}{{\sqrt {865} }} \approx 0,58$ $\sin α = \frac{C D}{A D} = \frac{24}{\sqrt{865}} \approx 0, 82; \cos α = \frac{A C}{A D} = \frac{17}{\sqrt{865}} \approx 0, 58$ và $\alpha \approx {55^0}$ $α \approx 55^{0}$

Bài 4.15

Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết HB = 3cm,HC = 6cm, $\widehat {HAC} = {60^0}$ $\hat{H A C} = 60^{0}$ . Hãy tính độ dài các cạnh (làm tròn đến cm) , số đo các góc của tam giác ABC (làm tròn đến độ) .

Lời giải:

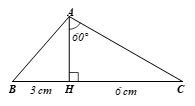
Cạnh BC = BH + HC = 3 + 6 = 9 cm

Ta có:

$\sin \widehat {HAC} = \frac{{HC}}{{AC}}$ $\sin \hat{H A C} = \frac{H C}{A C}$ hay $\sin {60^0} = \frac{6}{{AC}}$ $\sin 60^{0} = \frac{6}{A C}$ hay $AC = \frac{6}{{\sin {{60}^0}}} = 4\sqrt 3 cm$ $A C = \frac{6}{\sin 60^{0}} = 4 \sqrt{3} c m$

$\tan \widehat {HAC} = \frac{{HC}}{{AH}}$ $\tan \hat{H A C} = \frac{H C}{A H}$ hay $\tan {60^0} = \frac{6}{{AH}}$ $\tan 60^{0} = \frac{6}{A H}$ nên $AH = \frac{6}{{\tan {{60}^0}}} = 2\sqrt 3$ $A H = \frac{6}{\tan 60^{0}} = 2 \sqrt{3}$

Tam giác ABH vuông tại H nên ta có:

$A{B^2} = A{H^2} + B{H^2} = {\left( {2\sqrt 3 } \right)^2} + {3^2} = 21$ $A B^{2} = A H^{2} + B H^{2} = {(2 \sqrt{3})}^{2} + 3^{2} = 21$ hay A $B = \sqrt {21} cm$ $B = \sqrt{21} c m$ (vì AB > 0)

Bài 4.16

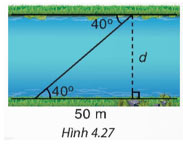
Tìm chiều rộng d của dòng sông trong Hình 4.27 (làm tròn đến m).

Luyện tập chung

Lời giải:

Chiều rộng của sông là $d = 50.\tan {40^0} \approx 42 m$ $d = 50. \tan 40^{0} \approx 42 m$

Vậy chiều rộng của sông khoảng 42 m

Bài 4.17

Tính các số liệu còn thiếu (dấu "?") ở Hình 4.28 với góc làm tròn đến độ, với độ dài làm tròn đến chữ số thập phân thứ nhất.

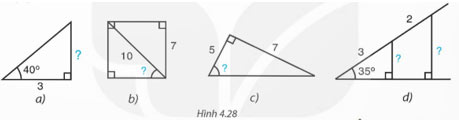
Luyện tập chung

a) Gọi độ dài cạnh cần tìm là x.

Ta có: tan40°= $\frac{x}{3}$ $\frac{x}{3}$ suy ra x = 3.tan40° ≈ 2,5.

b) Gọi số đo góc cần tìm là α.

Vì tứ giác đã cho có 3 góc vuông nên là hình chữ nhật. Do đó hai cạnh đối nhau có độ dài bằng nhau.

Ta có: sinα= $\frac{7}{10}$ $\frac{7}{10}$ =0,7 suy ra α ≈ 44°.

c) Gọi số đo góc cần tìm là β.

Ta có: tanα = $\frac{7}{5}$ $\frac{7}{5}$ suy ra β ≈ 54°.

d) Gọi độ dài cạnh góc vuông nhỏ và cạnh góc vuông lớn lần lượt là a, b.

Ta có:

⦁ sin35°= $\frac{a}{3}$ $\frac{a}{3}$ , suy ra a = 3.sin35° ≈ 1,7.

⦁ sin35°= $\frac{b}{5}$ $\frac{b}{5}$ , suy ra b = 5.sin35° ≈ 2,9.

Bài 4.18

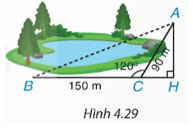
Một bạn muốn tính khoảng cách giữa hai điểm A và B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là CA = 90m,CB = 150m và $\widehat {ACB} = {120^0}$ $\hat{A C B} = 120^{0}$ (H.4.29) . Hãy tính AB giúp bạn.

Luyện tập chung

Lời giải:

Ta có: $\widehat {BCA} + \widehat {ACH} = {180^0}$ $\hat{B C A} + \hat{A C H} = 180^{0}$ (kề bù)

Nên $AH = AC.\sin \widehat {ACH} = 90.\sin 60 = 45\sqrt 3 m$ $A H = A C . \sin \hat{A C H} = 90. \sin 60 = 45 \sqrt{3} m$

$CH = AC.\cos \widehat {ACH} = 90.\cos {60^0} = 45 m$ $C H = A C . \cos \hat{A C H} = 90. \cos 60^{0} = 45 m$

Do đó BH = BC + CH = 150 + 45 = 195 m

Tam giác ABH vuông tại H nên $A{B^2} = A{H^2} + B{H^2}$ $A B^{2} = A H^{2} + B H^{2}$ (định lý Pythagore)

Thay số ta có $A{B^2} = {195^2} + {\left( {45\sqrt 3 } \right)^2} = 44100$ $A B^{2} = 195^{2} + {(45 \sqrt{3})}^{2} = 44100$ hay AB = 210 m.

Bài 4.19

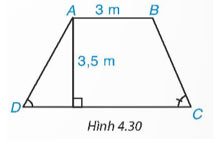
Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30). Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là tanD = 1,25. Độ dốc của sườn BC, tức là tanC = 1,5. Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).

Luyện tập chung

Lời giải:

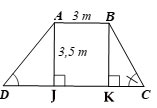
Kẻ BK vuông góc với DC tại K và AJ vuông góc với DC tại J nên hình thang có hai đường cao là AJ và BK; AB= JK = 3,5 m

Xét tứ giác ABKJ có AJ // BK; AJ = BK; $\widehat {AJK} = {90^0}$ $\hat{A J K} = 90^{0}$

Nên ABKJ là hình chữ nhật suy ra JK = AB = 3 m

Tam giác ADJ vuông tại J nên ta có:

$\tan \widehat D = \frac{{AJ}}{{DJ}}$ $\tan \hat{D} = \frac{A J}{D J}$ hay $1,25 = \frac{{3,5}}{{DJ}}$ $1, 25 = \frac{3, 5}{D J}$ suy ra $DJ = \frac{{3,5}}{{1,25}} = 2,8 m = 2,8 dm.$ $D J = \frac{3, 5}{1, 25} = 2, 8 m = 2, 8 d m .$

$A{D^2} = D{J^2} + A{J^2} = 3,{5^2} + 2,{8^2} = 20,09$ $A D^{2} = D J^{2} + A J^{2} = 3, 5^{2} + 2, 8^{2} = 20, 09$ hay $AD = \sqrt {20,09} \approx 4,5 m = 45 dm$ $A D = \sqrt{20, 09} \approx 4, 5 m = 45 d m$ (vì AD > 0)

Tam giác BKC vuông tại K nên ta có:

$\tan \widehat C = \frac{{BK}}{{KC}}$ $\tan \hat{C} = \frac{B K}{K C}$ hay $1,5 = \frac{{3,5}}{{KC}}$ $1, 5 = \frac{3, 5}{K C}$ suy ra $KC = \frac{{3,5}}{{1,5}} = \frac{7}{3} \approx 2,3 m = 28 dm.$ $K C = \frac{3, 5}{1, 5} = \frac{7}{3} \approx 2, 3 m = 28 d m .$

$B{C^2} = B{K^2} + K{C^2} = 3,{5^2} + 2,{3^2} = 17,54 hay BC = \sqrt {17,54} \approx 4,2 m =42 dm$ $B C^{2} = B K^{2} + K C^{2} = 3, 5^{2} + 2, 3^{2} = 17, 54 h a y B C = \sqrt{17, 54} \approx 4, 2 m = 42 d m$

(vì BC > 0)

Độ dài cạnh DC là $DC = DJ + JK + KC \approx 2,8 + 3 + 2,3 = 8,1 m$ $D C = D J + J K + K C \approx 2, 8 + 3 + 2, 3 = 8, 1 m$

Bài 4.20

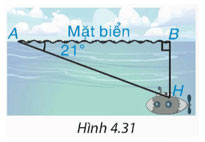
Trong một buổi tập trận, một tàu ngầm đang ở trên mặt biển bắt đầu di chuyển theo đường thẳng tạo với mặt nước biển một góc 21° để lặn xuống (H.4.31).

a) Khi tàu chuyển động theo hướng đó và đi được 200 m thì tàu ở độ sâu bao nhiêu so với mặt nước biển? (làm tròn đến m).

b) Giả sử tốc độ của tàu là 9 km/h thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu 200 m (tức là cách mặt nước biển 200 m)?

Luyện tập chung

Chia sẻ bởi:

Minh Ánh

Tải về

Bài trước

Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Bài sau

Bài tập cuối chương IV

Liên kết tải về

Toán 9 Luyện tập chung trang 79 255,5 KB Tải về

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!