Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn Giải Toán 9 Cánh diều tập 1 trang 74, 75, 76, 77, 78, 79, 80, 81

Cho tam giác MNP có MN = 5 cm, MP = 12 cm, NP = 13 cm. Chứng minh tam giác MNP vuông tại M. Từ đó, tính các tỉ số lượng giác của góc N.

Hướng dẫn giải:

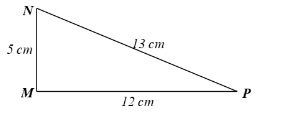
Xét ∆MNP, ta có: NP² = 13² = 169 và MN² + MP² = 5² + 12² = 169.

Suy ra NP² = MN² + MP².

Do đó ∆MNP vuông tại M (định lí Pythagore đảo).

Khi đó:

Bài 4

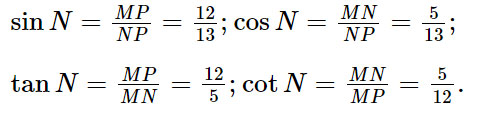
Mỗi tỉ số lượng giác sau đây bằng tỉ số lượng giác nào của góc 63°? Vì sao?

a) sin27°;

b) cos27°;

c) tan27°;

d) cot27°.

Hướng dẫn giải:

Vì 27° và 63° là hai góc phụ nhau nên ta có:

a) sin27° = cos63°;

b) cos27° = sin63°;

c) tan27° = cot63°;

d) cot27° = tan63°.

Bài 5

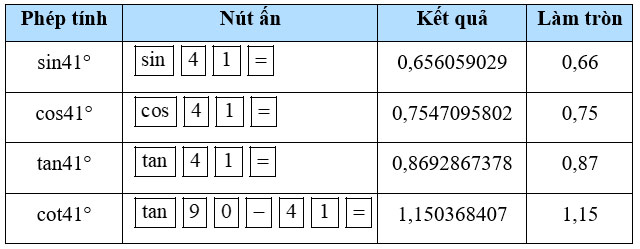
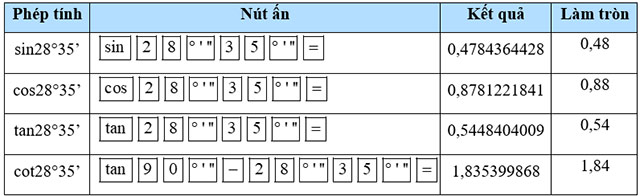
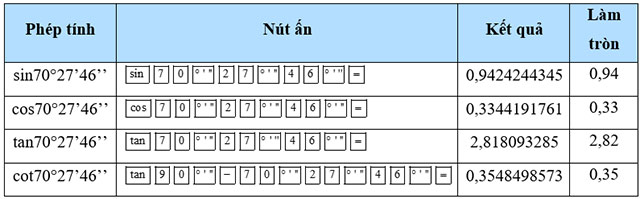
Sử dụng máy tính cầm tay để tính các tỉ số lượng giác của mỗi góc sau (làm tròn kết quả đến hàng phần trăm):

a) 41°;

b) 28°35’;

c) 70°27’46’’.

Hướng dẫn giải:

b)

c)

Bài 6

Sử dụng tỉ số lượng giác của hai góc phụ nhau, tính giác trị biểu thức:

A = sin25° + cos25° – sin65° – cos65°.

Hướng dẫn giải:

Vì25° và 65° là hai góc phụ nhau nên ta có sin25° = cos65° và sin65° = cos25°.

Do đó:

A = sin25° + cos25° – sin65° – cos65°

= cos65° + cos25° – cos25° – cos65°

= 0.

Bài 7

Cho góc nhọn α. Biết rằng, tam giác ABC vuông tại A có \(\widehat {B} =α\)

a) Biểu diễn các tỉ số lượng giác của góc nhọn α theo AB, BC, CA.

b) Chứng minh:

sin²α+cos²α = 1; \(\tan\ α=\frac{\sinα}{\cosα};\cos\ α=\frac{\cosα}{\sinα};\tan\ α.\cos\ α=1\)

Từ đó, tính giá trị biểu thức: S = sin²35° + cos²35°; T = tan61°.cot61°.

Bài 8

Hình 10 mô tả tia nắng mặt trời dọc theo AB tạo với phương nằm ngang trên mặt đất một góc α = \(\widehat {ABH}\). Sử dụng máy tính cầm tay, tính số đo góc α (làm tròn kết quả đến hàng đơn vị của độ) biết AH = 2 m, BH = 5 m.

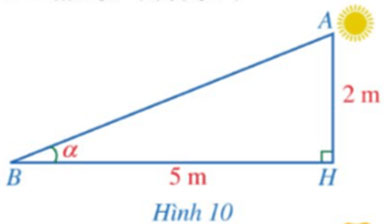
Hướng dẫn giải:

Xét ∆ABH vuông tại H, ta có tanα = tanB = \(\frac{AH}{BH}\) = \(\frac{2}{5}\)

Suy ra α ≈ 22°.