Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn và trải nghiệm website không quảng cáo
Tìm hiểu thêm »Giải bài tập Toán 9 Bài 18: Hàm số y = ax^2 (a ≠ 0) với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 9 Tập 2 Kết nối tri thức trang 4, 5, 6, 7, 8, 9. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.
Giải Toán 9 Bài 18 chi tiết phần câu hỏi, luyện tập, bài tập, đồng thời còn giúp các em hệ thống lại toàn bộ kiến thức trọng tâm của Bài 18 Chương VI: Hàm số y = ax2 (a ≠ 0), phương trình bậc hai một ẩn. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Cho hàm số y = 0,25x2. Hoàn thành bảng giá trị sau vào vở:

Hướng dẫn giải:
Thay lần lượt các giá trị x = –3; x = –2; …; x = 3 vào hàm số y = 0,25x2, ta được bảng giá trị:
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
|
y |
2,25 |
1 |
0,25 |
0 |
0,25 |
1 |
2,25 |
Cho hình lăng trụ đứng có đáy là hình vuông cạnh a (cm) và chiều cao 10 cm.
a) Viết công thức tính thể tích V của lăng trụ theo a và tính giá trị của V khi a = 2 cm.
b) Nếu độ dài cạnh đáy tăng lên hai lần thì thể tích của hình lăng trụ thay đổi thế nào?
Hướng dẫn giải:
a) Thể tích của hình lăng trụ đứng đó là: V = Bh = 10a2 (cm3).
Vậy công thức tính thể tích V của lăng trụ là V = 10a2 (cm3).
Khi a = 2 cm, thay vào công thức V = 10a2, ta được:
V = 10 . 22 = 40 (cm3).
Vậy V = 40 cm3 khi a = 2 cm.
b) Nếu độ dài cạnh đáy tăng lên hai lần thì độ dài cạnh đáy lúc này là 2a (cm).
Thể tích của hình lăng trụ lúc này là:
V’ = B’.h = 10 . (2a)2 = 40a2 = 4V (cm3).
Vậy nếu độ dài cạnh đáy tăng lên hai lần thì thể tích của hình lăng trụ tăng lên 4 lần.
Diện tích toàn phần S (cm2) của hình lập phương, tức là tổng diện tích xung quanh và diện tích của hai mặt đáy là một hàm số của độ dài cạnh a (cm).
a) Viết công thức của hàm số này.
b) Sử dụng công thức nhận được ở câu a để tính độ dài cạnh của một hình lập phương có diện tích toàn phần là 54 cm2.
Hướng dẫn giải:
a) Diện tích toàn phần của hình lập phương là:
S = 2 . a2 + 4 . a2 = 6a2 (cm2).
Vậy công thức của hàm số cần tìm là: S = 6a2 (cm2).
b) Ta có S = 54 cm2, thay vào công thức S = 6a2, ta được:
54 = 6a2, hay a2 = 9. Suy ra a = 3 (do a > 0).
Vậy một hình lập phương có diện tích toàn phần là 54 cm2 thì có độ dài cạnh bằng 3 cm.
Vẽ đồ thị của các hàm số sau:
a) y = 3x2.
b) ![]() \(y=-\frac{1}{3}x^2\)
\(y=-\frac{1}{3}x^2\)
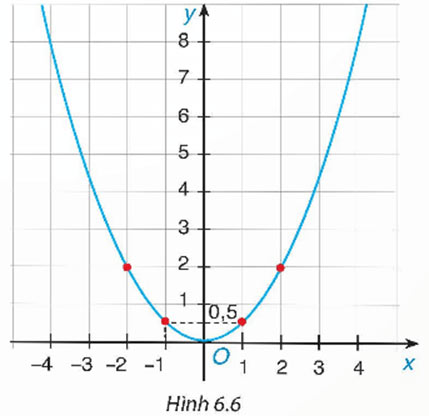
Biết rằng đường cong trong Hình 6.6 là một parabol y = ax2.
a) Tìm hệ số a.
b) Tìm tung độ của điểm thuộc parabol có hoành độ x = –2.
c) Tìm các điểm thuộc parabol có tung độ y = 8.
Hướng dẫn giải:
a) Do parabol y = ax2 trong Hình 6.6 đi qua điểm có tọa độ (2; 2) nên ta thay x = 2 và y = 2 vào hàm số y = ax2 thì được:
2 = a . 22, hay 4a = 2. Suy ra a = ![]() \(\frac{1}{2}\).
\(\frac{1}{2}\).
b) Trên Hình 6.6, ta thấy parabol đi qua điểm có tọa độ (–2; 2).
Vậy điểm thuộc parabol có hoành độ x = –2 thì có tung độ là 2.
c) Với a = ![]() \(\frac{1}{2}\) ta có hàm số
\(\frac{1}{2}\) ta có hàm số ![]() \(y=\frac{1}{2} x^{2}\)
\(y=\frac{1}{2} x^{2}\)
Thay y = 8 vào hàm số trên, ta được: ![]() \(8=\frac{1}{2} x^{2}\), hay x2 = 16.
\(8=\frac{1}{2} x^{2}\), hay x2 = 16.
Suy ra x = 4 hoặc x = –4.
Vậy các điểm thuộc parabol cần tìm là (–4; 8) và (4; 8).
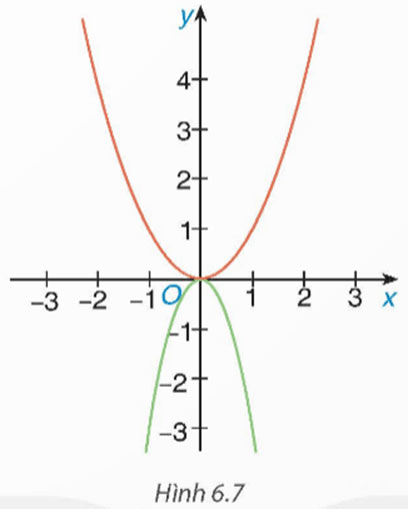
Trong Hình 6.7 có hai đường cong là đồ thị của hai hàm số y = –3x2 và y = x2. Hãy cho biết đường nào là đồ thị của hàm số y = –3x2.
Hướng dẫn giải:
Đồ thị hàm số y = ax2 (a ≠ 0) là đường cong parabol nằm phía trên trục hoành nếu a > 0 và nằm phía dưới trục hoành nếu a < 0.
Quan sát Hình 6,7, ta thấy đường cong màu đỏ nằm phía trên trục hoành và đường cong màu xanh nằm phía dưới trục hoành.
Mặt khác, hàm số y = –3x2 có hệ số a = –3 < 0. Do vậy, đường cong màu xanh chính là đồ thị của hàm số y = –3x2.
Một cổng vòm được thiết kế dạng parabol y = ax2 như Hình 6.8. Biết chiều rộng của chân cổng là AB = 6 m và chiều cao của cổng là OI = 4,5 m.
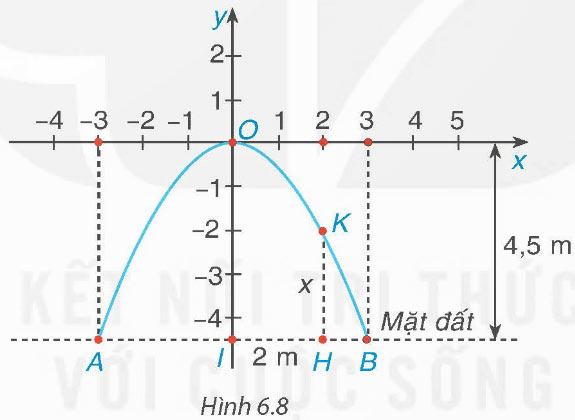
a) Tìm hệ số a dựa vào các dữ kiện trên. Từ đó, tính độ dài đoạn HK biết H cách điểm chính giữa cổng I là 2 m.
b) Để vận chuyển hàng qua cổng, người ta dự định sử dụng một xe tải có chiều rộng 2 m, chiều cao 3 m. Hỏi xe tải này có thể đi qua được cổng vòm đó hay không?
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: