Toán 8 Bài 7: Hình vuông Giải Toán 8 Cánh diều trang 116, 117, 118, 119

Giải Toán 8 Bài 7: Hình vuông là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Cánh diều tập 1 trang 116, 117, 118, 119.

Giải bài tập Toán 8 Cánh diều tập 1 trang 116 → 119 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 7 Chương V: Tam giác, tứ giác. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn nhé:

Giải Toán 8 Cánh diều Tập 1 trang 119

Bài 1

Cho hình thoi ABCD có AC = BD. Chứng minh ABCD là hình vuông.

Bài 2

Cho hình thoi ABCD có \(\widehat{A}\) = \(90^{\circ}\). Chứng minh ABCD là hình vuông.

Lời giải:

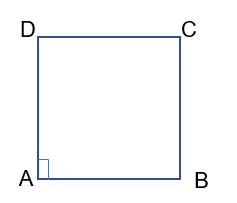
ABCD là hình thoi nên:

- Có các góc đối bằng nhau. Suy ra:

\(\widehat{C}\) = \(\widehat{A}\) = \(90^{\circ}\)

\(\widehat{B}\) = \(\widehat{D}\) = \(\frac{1}{2}\) (\(360^{\circ}\) - \(\widehat{C}\) - \(\widehat{A}\)) = \(\frac{1}{2}\) (\(360^{\circ}\)- \(90^{\circ}\)- \(90^{\circ}\)) = \(90^{\circ}\)

- 4 cạnh bằng nhau.

=> ABCD có 4 góc vuông và 4 cạnh bằng nhau nên là hình vuông. (đpcm)

Bài 3

Cho tam giác ABC vuông tại A có đường phân giác AD. Gọi H, K lần lượt là hình chiếu của D trên AB, AC. Chứng minh tứ giác AHDK là hình vuông.

Lời giải:

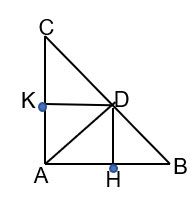
H, K lần lượt là hình chiếu của D trên AB, AC nên \(\widehat{DHA}=\widehat{DKA}=90^{\circ}\). Tứ giác AHDK có 3 góc vuông nên góc còn lại cũng là góc vuông. Vậy AHDK là hình chữ nhật.

Xét 2 tam giác vuông DHA và DKA có:

• \(\widehat{DAH}=\widehat{DAK}\) (AD là đường phân giác của góc A)
• AD chung

=> 2 tam giác vuông DHA và DKA bằng nhau theo trường hợp cạnh huyền, góc nhọn

=> 2 cạnh tương ứng AH = AK. Hình chữ nhật AHDK có 2 cạnh liền kề bằng nhau nên là hình vuông (đpcm)

Bài 4

Cho hai mảnh giấy, mỗi mảnh có đạng hình vuông với độ dài cạnh là 1 dm. Hãy trình bày cách cắt phép hai mảnh giấy đó để được một hình vuông có độ dài cạnh là \(\sqrt{2}\) dm.

Lời giải:

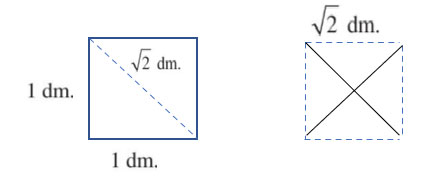
Cách làm:

- Gấp đôi mỗi mảnh giấy có dạng hình vuông theo đường kẻ chéo như hình đầu tiên, đường kẻ này sẽ có độ dài là \(\sqrt{2}\) dm (đúng với định lý pythagore). Sau đó dùng kéo cắt theo đường kẻ này ta sẽ có 4 mảnh giấy hình tam giác như nhau.

- Xếp 4 mảnh giấy tam giác này lại sao cho đường cắt của 4 mảnh tạo thành 4 cạnh của hình vuông mới, lúc này cạnh của hình vuông mới sẽ là \(\sqrt{2}\) dm

Bài 5

Bạn Thảo có một mảnh giấy có dạng hình tròn. Bạn Thảo đố bạn Minh: Không dùng thước thẳng và compa, làm thế nào có thể xác định tâm của hình tròn và chọn ra 4 vị trí trên đường tròn đó để chúng là 4 đỉnh của một hình vuông? Bạn Minh đã làm như sau:

Bước 1. Gấp mảnh giấy sao cho hai nửa hình tròn trùng khít nhau. Nét gấp thẳng tạo thành đường kính của hình tròn. Ta đánh dấu hai đầu mút của đường kính đó là hai điểm A, C.

Bước 2. Tiếp tục gấp mảnh giấy (có dạng nửa hình tròn) ở Bước 1 sao cho hai nửa mới của nửa hình tròn đó lại trùng khít nhau. Trải miếng bìa về dạng hình tròn ban đầu, ta được nét gấp mới là một đường kính khác của hình tròn.

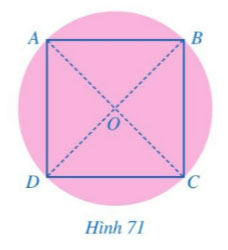
Bước 3. Ta đánh dấu giao điểm của hai đường kính là O và hai đầu mút của đường kính mới là hai điểm B, D. Khi đó O là tâm của hình tròn và tứ giác ABCD là hình vuông (Hình 7).

Em hãy giải thích cách làm của bạn Minh.

Lời giải:

Giải thích:

- Giao điểm của 2 đường kính của hình tròn sẽ cách tất cả các điểm trên đường tròn những khoảng cách như nhau gọi là bán kính. Và giao điểm O này chính là tâm của đường tròn.

- Với việc xác định các điểm mút như trên ta đi xét các tam giác sau:

Tam giác AOD và COB có:

• OA = OB; OD = OC (đều là bán kính đường tròn)
• Góc AOD và BOC bằng nhau (2 góc đối đỉnh)

=> Tam giác AOD và COB bằng nhau (c-g-c). Suy ra:

• AD = BC (1)
• \(\widehat{OAD}\) = \(\widehat{OCB}\) => AD//BC (2)

Tương tự vói 2 tam giác DOC và BOA. Suy ra:

• AB = DC. (3)
• \(\widehat{ODC}\) = \(\widehat{OBA}\) => AB//DC (4)

Từ (2) và (4) => ABCD là hình bình hành. Kết hợp với (1) và (2) => ABCD là hình vuông (hình bình hành có 2 cạnh đối song song và bằng nhau)