Toán 8 Bài 3: Đường trung bình của tam giác Giải Toán 8 Cánh diều tập 2 trang 62, 63, 64, 65

Bài trước

Mục lục

Bài sau

Giải Toán 8 Bài 3: Đường trung bình của tam giác là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Cánh diều tập 2 trang 62, 63, 64, 65.

Giải bài tập Toán 8 Cánh diều tập 2 trang 63 → 65 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 3 Chương VIII: Tam giác đồng dạng, hình đồng dạng. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Toán 8 Bài 3: Đường trung bình của tam giác Cánh diều

Giải Toán 8 Cánh diều Tập 2 trang 65

Giải Toán 8 Cánh diều Tập 2 trang 65

Bài 1

Cho tam giác ABC có M là trung điểm của AB, điểm N thuộc cạnh AC thỏa mãn MN // BC. Chứng minh NA = NC và MN = $\frac{1}{2}$ $\frac{1}{2}$BC.

Lời giải:

- Vì MN // BC nên theo định lí Thalès ta có: $\frac{AM}{MB}=\frac{AN}{NC}$ $\frac{AM}{MB}=\frac{AN}{NC}$

Mà AM = MB (M là trung điểm của AB)

Suy ra: AN = NC.

- Vì MN // BC nên ta có: $\frac{AM}{AB}=\frac{MN}{BC}$ $\frac{AM}{AB}=\frac{MN}{BC}$

Mà AM = $\frac{1}{2}$ $\frac{1}{2}$AB (M là trung điểm của AB)

Do đó: MN = $\frac{1}{2}$ $\frac{1}{2}$BC.

Bài 2

Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB sao cho AP = PN = NB. Gọi Q là giao điểm của AM và CP. Chứng minh:

a) MN // CP;

b) AQ = QM;

c) CP = 4PQ.

Lời giải:

a) Tam giác BCP có: PN = NB; BM = MC (M là trung điểm của BC)

Suy ra: $\frac{BN}{NP}=\frac{BM}{MC}$ $\frac{BN}{NP}=\frac{BM}{MC}$

Do đó: MN // CP (Định lí Thalès).

b) Tam giác AMN có: MN // PQ (MN // CP, Q $\in$ $\in$ CP)

Suy ra: $\frac{AP}{PN}=\frac{AQ}{QM}$ $\frac{AP}{PN}=\frac{AQ}{QM}$

Mà AP = PN

Do đó: AQ = QM.

c) Do MN // PQ nên $\frac{PQ}{NM}=\frac{AP}{AN}$ $\frac{PQ}{NM}=\frac{AP}{AN}$

Mà AP = $\frac{1}{2}$ $\frac{1}{2}$AN

Suy ra: PQ = $\frac{1}{2}$ $\frac{1}{2}$NM. (1)

Do MN // CP nên $\frac{NM}{CP}=\frac{BN}{BP}$ $\frac{NM}{CP}=\frac{BN}{BP}$

Mà BN = $\frac{1}{2}$ $\frac{1}{2}$BP

Suy ra: NM = $\frac{1}{2}$ $\frac{1}{2}$CP. (2)

Từ (1)(2) suy ra: PQ = $\frac{1}{2}$ $\frac{1}{2}$. $\frac{1}{2}$ $\frac{1}{2}$CP = $\frac{1}{4}$ $\frac{1}{4}$CP hay CP = 4PQ.

Bài 2

Bài 3

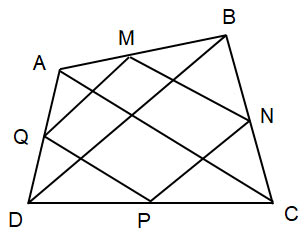
Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

a) Chứng minh tứ giác MNPQ là hình bình hành.

b) Cho AC = BD. Chứng minh tứ giác MNPQ là hình thoi.

c) Cho AC $\perp$ $\perp$ BD. Chứng minh tứ giác MNPQ là hình chữ nhật.

Lời giải:

a) Tam giác ABD có: M, Q lần lượt là trung điểm của AB, DA.

Suy ra: MQ là đường trung bình nên MQ // BD (1)

Tam giác BDC có: N, P lần lượt là trung điểm của BC, CD.

Suy ra: NP là đường trung bình nên NP // BD (2)

Từ (1)(2) suy ra: MQ // NP (3)

Tam giác ABC có: M, N lần lượt là trung điểm của AB, BC.

Suy ra: MN là đường trung bình nên MN // AC (4)

Tam giác ADC có: P, Q lần lượt là trung điểm của CD, DA.

Suy ra: PQ là đường trung bình nên PQ // AC (5)

Từ (4)(5) suy ra: MN // PQ (6)

Từ (3)(6) suy ra: MNPQ là hình bình hành.

b) MQ là đường trung bình của tam giác ABD, suy ra MQ = $\frac{1}{2}$ $\frac{1}{2}$BD

NP là đường trung bình của tam giác BDC, suy ra NP = $\frac{1}{2}$ $\frac{1}{2}$BD

MN là đường trung bình của tam giác ABC, suy ra MN = $\frac{1}{2}$ $\frac{1}{2}$AC

PQ là đường trung bình của tam giác ADC, suy ra PQ = $\frac{1}{2}$ $\frac{1}{2}$AC

Mà AC = BD

Do đó: MQ = NP = MN = PQ

Mà MNPQ là hình bình hành (cmt)

Suy ra: MNPQ là hình thoi.

c) Ta có: MQ // BD; MN // AC

Mà AC $\perp$ $\perp$ BD

Suy ra: MQ $\perp$ $\perp$ MN

Mà MNPQ là hình bình hành (chứng minh câu a)

Do đó: MNPQ là hình chữ nhật.

Bài 3

Bài 4

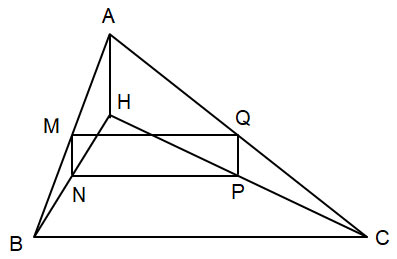
Cho tam giác ABC nhọn có H là trực tâm. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AB, BH, HC, CA. Chứng minh tứ giác MNPQ là hình chữ nhật.

Lời giải:

Tam giác ABH có: M, N lần lượt là trung điểm của AB, BH.

Suy ra: MN là đường trung bình nên MN // AH và MN = $\frac{1}{2}$ $\frac{1}{2}$AH (1)

Tam giác ACH có: P, Q lần lượt là trung điểm của CH, AC.

Suy ra: PQ là đường trung bình nên PQ // AH và PQ = $\frac{1}{2}$ $\frac{1}{2}$AH (2)

Từ (1)(2) suy ra: MN // PQ và MN = PQ.

Do đó: MNPQ là hình bình hành (3)

Ta có: MN // AH

Mà AH $\perp$ $\perp$ BC (H là trực tâm tam giác ABC)

Suy ra: MN $\perp$ $\perp$ BC

Mà MQ // BC (MQ là đường trung bình của tam giác ABC)

Do đó: MN $\perp$ $\perp$ MQ (4)

Từ (3)(4) suy ra: MNPQ là hình chữ nhật.

Bài 4

Bài 5

Trong Hình 36, ba cạnh màu vàng AB, BC, CA gợi nên hình ảnh tam giác ABC và đoạn thẳng màu xanh MN là một đường trung bình của tam giác đó. Bạn Duyên đứng ở phía dưới đo khoảng cách giữa hai chân cột số 1 và số 2, từ đó ước lượng được độ dài đoạn thẳng MN khoảng 4,5 m. Khoảng cách giữa hai mép dưới của mái được tính bằng độ dài đoạn thẳng BC. Hỏi khoảng cách đó khoảng bao nhiêu mét?

Bài 5