Toán 8 Bài 1: Phương trình bậc nhất một ẩn Giải Toán 8 Cánh diều tập 2 trang 39, 40, 41, 42, 43, 44

Bài trước

Mục lục

Bài sau

Giải Toán 8 Bài 1: Phương trình bậc nhất một ẩn là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Cánh diều tập 2 trang 39, 40, 41, 42, 43, 44.

Giải bài tập Toán 8 Cánh diều tập 2 trang 39 → 44 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 1 Chương VII: Phương trình bậc nhất một ẩn. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Toán 8 Bài 1: Phương trình bậc nhất một ẩn Cánh diều

Giải Toán 8 Cánh diều Tập 2 trang 43, 44

Giải Toán 8 Cánh diều Tập 2 trang 43, 44

Bài 1

Kiểm tra xem số nào là nghiệm của phương trình tương ứng sau đây.a) 3x + 9 = 0 với x = 3; x = -3.b) 2 - 2x = 3x + 1 với x = $-\frac{1}{5}$ $-\frac{1}{5}$; x = $\frac{1}{5}$ $\frac{1}{5}$.

Lời giải:

a) Thay x = 3 vào phương trình, ta có: 3.3 + 9 = 18 $\neq$ $\neq$ 0.

Thay x = -3 vào phương trình, ta có: 3.(-3) + 9 = 0.

Vậy x = 3 không là nghiệm của phương trình, x = -3 là nghiệm của phương trình.

b) Thay x = $-\frac{1}{5}$ $-\frac{1}{5}$ vào phương trình, ta có: 2 - 2.( $-\frac{1}{5}$ $-\frac{1}{5}$) $\neq$ $\neq$ 3.( $-\frac{1}{5}$ $-\frac{1}{5}$) + 1.

Thay x = $\frac{1}{5}$ $\frac{1}{5}$ vào phương trình, ta có: 2 - 2.( $\frac{1}{5}$ $\frac{1}{5}$) = 3.( $\frac{1}{5}$ $\frac{1}{5}$) + 1.

Vậy x = $-\frac{1}{5}$ $-\frac{1}{5}$ không là nghiệm của phương trình, x = $\frac{1}{5}$ $\frac{1}{5}$ là nghiệm của phương trình.

Bài 2

Tìm chỗ sai trong mỗi lời giải sau và giải lại cho đúng:

a) 5 - (x + 8) = 3x + 3(x - 9)

5 - x + 8 = 3x + 3x - 27

13 - x = 6x - 27

-x - 6x = -27 + 13

-7x = -14

x = (-14) : (-7)

x = 2.

Vậy phương trình có nghiệm x = 2.

b) 3x - 18 + x = 12 - (5x + 3)

4x - 18 = 12 - 5x - 3

4x + 5x = 9 - 18

9x = -9

x = (-9) : 9

x = -1.

Vậy phương trình có nghiệm x = -1.

Lời giải:

a) Bài toán giải sai ở bước thứ hai: -(x + 8) bỏ ngoặc ra thì phải là - x - 8, chứ không phải là - x + 8; và ở bước thứ tư: 13 chuyển vế thì phải đổi dấu thành - 13, chứ không phải là + 13.

Giải lại:

5 - (x + 8) = 3x + 3(x - 9)

5 - x - 8 = 3x + 3x - 27

-3 - x = 6x - 27

-x - 6x = -27 + 3

-7x = -24

x = $\frac{24}{7}$ $\frac{24}{7}$.

Vậy phương trình có nghiệm x = $\frac{24}{7}$ $\frac{24}{7}$.

b) Bài toán giải sai ở bước thứ ba: -18 chuyển vế thì phải đổi dấu thành 18, chứ không phải là - 18.

Giải lại:

3x - 18 + x = 12 - (5x + 3)

4x - 18 = 12 - 5x - 3

4x + 5x = 9 + 18

9x = 27

x = 3.

Vậy phương trình có nghiệm x = 3.

Bài 3

Giải các phương trình:

a) 6x + 4 = 0;

b) -14x - 28 = 0;

c) $\frac{1}{3}$ $\frac{1}{3}$x - 5 = 0;

d) 3y - 1 = -y + 19;

e) -2(z + 3) - 5 = z + 4;

g) 3(t - 10) = 7(t - 10).

Lời giải:

a) 6x + 4 = 0

6x = -4

x = -4 : 6

x = $\frac{-2}{3}$ $\frac{-2}{3}$

Vậy phương trình có nghiệm $\frac{-2}{3}$ $\frac{-2}{3}$.

b) -14x - 28 = 0

-14x = 28

x = 28 : (-14)

x = -2.

Vậy phương trình có nghiệm x = -2.

c) $\frac{1}{3}$ $\frac{1}{3}$x - 5 = 0

$\frac{1}{3}$ $\frac{1}{3}$x = 5

x = 5 : $\frac{1}{3}$ $\frac{1}{3}$

x = 15

Vậy phương trình có nghiệm x = 15.

d) 3y - 1 = -y + 19

3y + y = 19 + 1

4y = 20

y = 5

Vậy phương trình có nghiệm y = 5.

e) -2(z + 3) - 5 = z + 4

-2z - 6 - 5 = z + 4

-2z - 11 = z + 4

-2z - z = 4 + 11

-3z = 15

z = 15 : (-3)

z = -5

Vậy phương trình có nghiệm z = -5.

g) 3(t - 10) = 7(t - 10)

3t - 30 = 7t - 70

3t - 7t = -70 + 30

-4t = -40

t = -40 : (-4)

t = 10

Vậy phương trình có nghiệm t = 10.

Bài 4

Giải các phương trình:

a) $\frac{5x-2}{3}=\frac{5-3x}{2}$ $\frac{5x-2}{3}=\frac{5-3x}{2}$;

b) $\frac{10x+3}{12}=1+\frac{6+8x}{9}$ $\frac{10x+3}{12}=1+\frac{6+8x}{9}$;

c) $\frac{7x-1}{6}+2x=\frac{16-x}{5}$ $\frac{7x-1}{6}+2x=\frac{16-x}{5}$.

Lời giải:

a) $\frac{5x-2}{3}=\frac{5-3x}{2}$ $\frac{5x-2}{3}=\frac{5-3x}{2}$

2(5x - 2) = 3(5 - 3x)

10x - 4 = 15 - 9x

10x + 9x = 15 + 4

19x = 19

x = 19 : 19

x = 1

Vậy phương trình có nghiệm x = 1.

b) $\frac{10x+3}{12}=1+\frac{6+8x}{9}$ $\frac{10x+3}{12}=1+\frac{6+8x}{9}$

$\frac{10x+3}{12}$ $\frac{10x+3}{12}$ = $\frac{9+6+8x}{9}$ $\frac{9+6+8x}{9}$

$\frac{10x+3}{12}$ $\frac{10x+3}{12}$ = $\frac{15+8x}{9}$ $\frac{15+8x}{9}$

9(10x + 3) = 12(15 + 8x)

90x + 27 = 180 + 96x

90x - 96x = 180 - 27

-6x = 153

x = 153 : (-6)

x = $\frac{-51}{2}$ $\frac{-51}{2}$

Vậy phương trình có nghiệm x = $\frac{-51}{2}$ $\frac{-51}{2}$.

c) $\frac{7x-1}{6}+2x=\frac{16-x}{5}$ $\frac{7x-1}{6}+2x=\frac{16-x}{5}$

$\frac{7x-1+12x}{6}=\frac{16-x}{5}$ $\frac{7x-1+12x}{6}=\frac{16-x}{5}$

$\frac{19x-1}{6}=\frac{16-x}{5}$ $\frac{19x-1}{6}=\frac{16-x}{5}$

5(19x -1) = 6(16 - x)

95x - 5 = 96 - 6x

95x + 6x = 96 + 5

101x = 101

x = 101 : 101

x = 1

Vậy phương trình có nghiệm x = 1.

Bài 5

Tìm x, biết tứ giác ABCD ở Hình 2 là hình vuông.

Bài 5

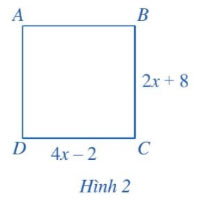
Lời giải:

Tứ giác ABCD là hình vuông nên suy ra: 2x + 8 = 4x - 2.

Ta có: 2x + 8 = 4x - 2

2x - 4x = -2 - 8

-2x = -10

x = -10 : (-2)

x = 5

Vậy x = 5.

Bài 6

Hình tam giác và hình chữ nhật ở Hình 3 có cùng chu vi. Viết phương trình biểu thị sự bằng nhau của chu vi hình tam giác, hình chữ nhật đó và tìm x.

Bài 6

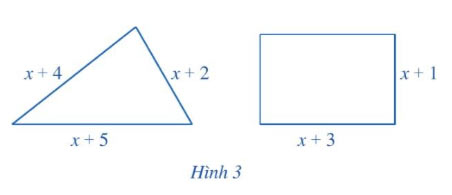
Lời giải:

Chu vi hình tam giác là: x + 4 + x + 2 + x + 5 = 3x + 11

Chu vi hình chữ nhật là: 2(x + 3 + x + 1) = 2(2x + 4)

Vì chu vi hình tam giác bằng chu vi hình chữ nhật nên ta có phương trình:

3x + 11 = 2(2x + 4)

3x + 11 = 4x + 8

3x - 4x = 8 - 11

-x = -3

x = 3

Vậy x = 3.

Bài 7

Trong phòng thí nghiệm, chị Loan sử dụng cân Roberval để cân: bên đĩa thứ nhất đặt một quả cân nặng 500 g; bên đĩa thứ hai đặt hai vật cùng cân nặng x (g) và ba quả cân nhỏ, mỗi quả cân đó nặng 50 g. Chị Loan thấy cân thăng bằng. Viết phương trình ẩn x biểu thị sự thăng bằng của cân khi đó.

Lời giải:

Ta có phương trình: 500 = 2x + 150.

Bài 8

Hình 4 mô tả một đài phun nước. Tốc độ ban đầu của nước là 48 ft/s (ft là một đơn vị đo độ dài với 1 ft = 0,3048 m). Tốc độ v (ft/s) của nước tại thời điểm t (s) được cho bởi công thức: v = 48 - 32t. Tìm thời gian để nước đi từ mặt đài phun nước đến khi đạt được độ cao tối đa.

Bài 8