Toán 7 Bài 1: Tập hợp các số hữu tỉ Giải Toán lớp 7 trang 6 sách Chân trời sáng tạo - Tập 1

Giải bài tập SGK Toán 7 Tập 1 Chân trời sáng tạo trang 6, 7, 8, 9, 10 giúp các em học sinh lớp 7 xem gợi ý giải các bài tập của Bài 1: Tập hợp các số hữu tỉ để củng cố kiến thức, rèn luyện kỹ năng giải môn Toán.

Thông qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 1 Chương I: Số hữu tỉ trong sách giáo khoa Toán 7 Tập 1 Chân trời sáng tạo. Đồng thời, cũng giúp thầy cô tham khảo để soạn giáo án cho học sinh của mình theo chương trình mới. Mời thầy cô và các em cùng theo dõi bài viết dưới dây của Download.vn:

Phần Thực hành

Thực hành 1 trang 6 Toán 7 tập 1

Vì sao các số \(- 0,33;{\text{ }}0;{\text{ }}3\frac{1}{2};{\text{ }}0,25\) là các số hữu tỉ?

Hướng dẫn giải:

Số hữu tỉ là số được viết dưới dạng phân số \(\frac{a}{b}\), với \(a,b \in \mathbb{Z},b \ne 0\)

Các phân số bằng nhau biểu diễn cũng một số hữu tỉ.

Trên trục số, mỗi số hữu tỉ được biểu diễn bởi một điểm. Điểm biểu diễn số hữu tỉ x được gọi là điểm x.

Với hai số hữu tỉ bất kì x, y nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.

Ta có: \(- 0,33 = \frac{{ - 33}}{{100}}\)

Vì \(- 33 \in \mathbb{Z};100 \in \mathbb{Z},100 \ne 0\) => \(\frac{{ - 33}}{{100}} \in \mathbb{Q}\)

Vậy 0,33 là số hữu tỉ.

Lời giải:

Ta có: \(0 = \frac{0}{1}\)

Vì \(0 \in \mathbb{Z};1 \in \mathbb{Z},1 \ne 0\) => \(0 \in \mathbb{Q}\)

Vậy 0 là số hữu tỉ.

Ta có: \(3\frac{1}{2} = \frac{7}{2}\)

Vì \(7 \in \mathbb{Z};2 \in \mathbb{Z},2 \ne 0\) => \(3\frac{1}{2} \in \mathbb{Q}\)

Vậy \(3\frac{1}{2}\) là số hữu tỉ.

Ta có: \(0,25 = \frac{{25}}{{100}}\)

Vì \(25 \in \mathbb{Z};100 \in \mathbb{Z},100 \ne 0\)=> \(0,25 \in \mathbb{Q}\)

Vậy 0,25 là số hữu tỉ.

Thực hành 2 trang 6 Toán 7 tập 1

Cho các số hữu tỉ: \(\frac{{ - 7}}{{12}};\frac{4}{5};5,12; - 3;\frac{0}{{ - 3}}; - 3,75\)

a) So sánh \(\frac{{ - 7}}{{12}}\) với \(- 3,75;\frac{0}{{ - 3}};\frac{4}{5}\)

b) Trong các số hữu tỉ đã cho, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?

Hướng dẫn giải

Trên trục số, mỗi số hữu tỉ được biểu diễn bởi một điểm. Điểm biểu diễn số hữu tỉ x được gọi là điểm x.

Với hai số hữu tỉ bất kì x, y nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.

Hai số hữu tỉ có điểm biểu diễn trên trục số cách đều và nằm về hai phía điểm gốc O là hai số đối nhau, số này gọi là số đối của số kia.

Lời giải:

a) Ta có: \(- 3,75 = \frac{{ - 375}}{{100}} = \frac{{ - 15}}{4};\frac{0}{{ - 3}} = 0\)

\(\frac{4}{5}\) là số hữu tỉ dương => \(\frac{4}{5} > 0\)

\(\frac{{ - 15}}{4};\frac{{ - 7}}{{12}}\) là các số hữu tỉ âm luôn nhỏ hơn 0

\(\frac{{ - 15}}{4} = \frac{{ - 15.3}}{{4.3}} = \frac{{ - 45}}{{12}}\)

Ta có: -45 < -7 => \(\frac{{ - 15}}{4} < \frac{{ - 7}}{{12}}\)

=> \(- 3,75 < \frac{{ - 7}}{{12}} < 0\)

Vậy \(- 3,75 < \frac{{ - 7}}{{12}} < 0 < \frac{4}{5}\)

b) Các số hữu tỉ dương: \(\frac{4}{5};5,12\)

Các số hữu tỉ âm: \(\frac{{ - 7}}{{12}}; - 3; - 3,75\)

Số \(\frac{0}{{ - 3}}\) không là số hữu tỉ dương cũng không là số hữu tỉ âm

Thực hành 3 trang 7 Toán 7 tập 1

a) Các điểm M, N, P trong Hình 6 biểu diễn các số hữu tỉ nào?

b) Biểu diễn các số hữu tỉ sau trên trục số: \(- 0,75;{\text{ }}\frac{1}{{ - 4}};{\text{ 1}}\frac{1}{4}\)

Hướng dẫn giải:

a) - Đoạn thẳng đơn vị chia thành 3 đoạn thẳng bằng nhau, đơn vị mới bằng \(\frac{1}{3}\) đơn vị cũ.

Quan sát phần hình vẽ phía bên phải điểm O:

+ Điểm M nằm cách O một đoạn bằng 5 đơn vị mới.

=> Điểm M biểu diễn số hữu tỉ: \(\frac{5}{3}\)

Quan sát phần hình vẽ phía bên trái điểm O (các số hữu tỉ là các số âm)

+ Điểm N nằm cách O một đoạn bằng 1 đơn vị mới.

=> Điểm N biểu diễn số hữu tỉ: \(- \frac{1}{3}\)

+ Điểm P nằm cách O một đoạn bằng 4 đơn vị mới

=> Điểm P biểu diễn số hữu tỉ: \(- \frac{4}{3}\)

b) Ta có: \(- 0,75 = \frac{{75}}{{100}} = \frac{3}{4};1\frac{1}{4} = \frac{5}{4}\)

Biểu diễn các số hữu tỉ như sau:

Thực hành 4 trang 8 Toán 7 tập 1

Tìm số đối của mỗi số sau: \(7;{\text{ }}\frac{{ - 5}}{9};{\text{ }} - 0,75;{\text{ }}0;{\text{ }}1\frac{2}{3}\)

Hướng dẫn giải:

Số đối của số hữu tỉ 7 là số -7

Số đối của số hữu tỉ \(- \frac{5}{9}\) là số \(\frac{5}{9}\)

Số đối của số hữu tỉ -0,75 là số 0,75

Số đối của số hữu tỉ 0 là số 0

Ta có: \(1\frac{2}{3} = \frac{5}{3}\)

Số đối của số hữu tỉ \(1\frac{2}{5}\) là số \(- \frac{5}{3}\)

Phần Vận dụng

Vận dụng 1 trang 6 Toán 7 tập 1

Viết các số đo các đại lượng sau dưới dạng \(\frac{a}{b}\) với \(a,b \in \mathbb{Z},\,\,b \ne 0\).

a) 2,5kg đường

b) 3,8 m dưới mực nước biển

Gợi ý đáp án:

a) \(2,5\,\,kg = \frac{{25}}{{10}}\,\,kg\, = \,\frac{5}{2}\,kg\)

b) \(3,8\,m = \frac{{38}}{{10}}\,m\, = \frac{{19}}{5}\,m\)

Vận dụng 2 trang 9 Toán 7 tập 1

Bạn Hồng đã phát biểu “4,1 lớn hơn 3,5. Vì thế -4,1 cũng lớn hơn -3,5”. Theo em, phát biểu của bạn Hồng có đúng không? Tại sao?

Gợi ý đáp án:

Ta có:

\(\begin{matrix} - 4,1 = \dfrac{{ - 41}}{{10}} \hfill \\ - 3,5 = \dfrac{{ - 35}}{{10}} \hfill \\ \end{matrix}\)

Do -41 < -35 => \(\frac{{ - 41}}{{10}} < \frac{{ - 35}}{{10}}\)

=> 4,1 < -3,5

Vậy phát biểu của bạn Hồng là sai.

Phần Bài tập

Bài 1 trang 9 Toán 7 tập 1

Thay dấu ? bằng kí hiệu “∈” hoặc “ ∉” thích hợp:

\(- 7?\mathbb{N}\)	\(- 17?\mathbb{Z}\)	\(- 38?\mathbb{Q}\)
\(\frac{4}{5}?\mathbb{Z}\)	\(\frac{4}{5}?\mathbb{Q}\)	\(0,25?\mathbb{Z}\)	\(3,25?\mathbb{Q}\)

Gợi ý đáp án:

Ta điền các dấu thích hợp vào dấu hỏi chấm như sau:

\(- 7 \notin \mathbb{N}\)	\(- 17 \notin \mathbb{Z}\)	\(- 38 \in \mathbb{Q}\)
\(\frac{4}{5} \notin \mathbb{Z}\)	\(\frac{4}{5} \notin \mathbb{Q}\)	\(0,25 \notin \mathbb{Z}\)	\(3,25 \notin \mathbb{Q}\)

Bài 2 trang 9 Toán 7 tập 1

a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ \(\frac{{ - 5}}{9}\)?

\(\frac{{ - 10}}{{18}};\frac{{10}}{{18}};\frac{{15}}{{ - 27}}; - \frac{{20}}{{36}};\frac{{ - 25}}{{27}}\)

b) Tìm số đối của mỗi số sau: \(12;{\text{ }} - \frac{5}{9};{\text{ }} - 0,375;{\text{ }}0;{\text{ }}2\frac{2}{5}\)

Gợi ý đáp án:

a) Ta có:

\(\begin{matrix} \dfrac{{ - 10}}{{18}} = \dfrac{{ - 10:2}}{{18:2}} = \dfrac{{ - 5}}{9} \hfill \\ \dfrac{{10}}{{18}} = \dfrac{{10:2}}{{18:2}} = \dfrac{5}{9} \hfill \\ \dfrac{{15}}{{ - 27}} = \dfrac{{15:3}}{{ - 27:3}} = \dfrac{5}{{ - 9}} = \dfrac{{ - 5}}{9} \hfill \\ - \dfrac{{20}}{{36}} = \dfrac{{ - 20:4}}{{36:4}} = \dfrac{{ - 5}}{9} \hfill \\ \end{matrix}\)

Vậy những phân số nào biểu diễn số hữu tỉ \(\frac{{ - 5}}{9}\) là \(\frac{{ - 10}}{{18}};\frac{{15}}{{ - 27}}; - \frac{{20}}{{36}}\)

b) Số đối của số hữu tỉ 12 là số -12

Số đối của số hữu tỉ \(\frac{{ - 5}}{9}\) là số \(\frac{5}{9}\)

Số đối của số hữu tỉ -0,375 là số 0,375

Số đối của số hữu tỉ 0 là số 0

Ta có: \(2\frac{2}{5} = \frac{{12}}{5}\)

Số đối của số hữu tỉ \(2\frac{2}{5}\) là số \(- \frac{{12}}{5}\)

Bài 3 trang 9 Toán 7 tập 1

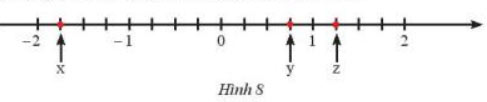
a) Các điểm A; B; C trong Hình 8 biểu diễn số hữu tỉ nào?

b) Biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};1\frac{1}{5};\frac{3}{5}; - 0,8\) trên trục số.

Gợi ý đáp án:

a) - Đoạn thẳng đơn vị chia thành 4 đoạn thẳng bằng nhau, đơn vị mới bằng \(\frac{1}{4}\) đơn vị cũ.

Quan sát phần hình vẽ phía bên phải điểm O:

+ Điểm y nằm cách O một đoạn bằng 3 đơn vị mới.

=> Điểm y biểu diễn số hữu tỉ: \(\frac{3}{4}\)

+ Điểm z nằm cách O một đoạn bằng 5 đơn vị mới

=> Điểm z biểu diễn số hữu tỉ: \(\frac{5}{4}\)

Quan sát phần hình vẽ phía bên trái điểm O (các số hữu tỉ là các số âm)

+ Điểm x nằm cách O một đoạn bằng 7 đơn vị mới.

=> Điểm x biểu diễn số hữu tỉ: \(\frac{{ - 7}}{4}\)

b) Ta có: \(1\frac{1}{5} = \frac{6}{5}; - 0,8 = \frac{{ - 8}}{{10}} = \frac{{ - 4}}{5}\)

Biểu diễn các số hữu tỉ như sau:

Bài 4 trang 10 Toán 7 tập 1

a) Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?

\(\frac{5}{{12}}; - \frac{4}{5};2\frac{2}{3}; - 2;\frac{0}{{234}}; - 0,32\)

b) Hãy sắp xếp các số trên theo thứ tự từ nhỏ đến lớn.

Gợi ý đáp án:

a) Ta có:

\(\begin{matrix} \dfrac{5}{{12}} > 0 \hfill \\ - \dfrac{4}{5} < 0 \hfill \\ 2\dfrac{2}{3} > 0 \hfill \\ - 2 < 0 \hfill \\ \dfrac{0}{{234}} = 0 \hfill \\ - 0,32 < 0 \hfill \\ \end{matrix}\)

Các số hữu tỉ dương là: \(\frac{5}{{12}};2\frac{2}{3}\)

Các số hữu tỉ âm là: \(- \frac{4}{5}; - 2; - 0,32\)

Số \(\frac{0}{{234}}\) không là số hữu tỉ dương cũng không là số hữu tỉ âm.

b) Thực hiện so sánh các nhóm số đã phân loại ở câu a

Nhóm các số hữu tỉ dương là: \(\frac{5}{{12}};2\frac{2}{3}\)

Ta có: \(2\frac{2}{3} = \frac{8}{3} = \frac{{32}}{{12}}\)

\(\frac{5}{{12}} < \frac{{32}}{{12}} \Rightarrow \frac{5}{{12}} < 2\frac{2}{3}\)

Nhóm các số hữu tỉ âm là: \(- \frac{4}{5}; - 2; - 0,32\)

Ta có:

\(\begin{matrix} - 0,32 = \dfrac{{ - 32}}{{100}} = \dfrac{{ - 8}}{{25}} \hfill \\ - \dfrac{4}{5} = \dfrac{{ - 20}}{{25}} \hfill \\ - 2 = \dfrac{{ - 50}}{{25}} \hfill \\ \end{matrix}\)

=> \(\frac{{ - 50}}{{25}} < \frac{{ - 20}}{{25}} < \frac{{ - 8}}{{25}}\)

=> \(- 2 < - \frac{4}{5} < - 0,32\)

Vì số hữu tỉ âm luôn nhỏ hơn 0 và nhỏ hơn số hữu tỉ dương nên ta có:

\(- 2 < - \frac{4}{5} < - 0,32 < \frac{0}{{234}} < \frac{5}{{12}} < 2\frac{2}{3}\)

Vậy sắp xếp các số trên theo thứ tự từ nhỏ đến lớn như sau:

\(- 2; - \frac{4}{5}; - 0,32;\frac{0}{{234}};\frac{5}{{12}};2\frac{2}{3}\)

Bài 5 trang 10 Toán 7 tập 1

So sánh các cặp số hữu tỉ sau:

Gợi ý đáp án:

a) \(\frac{2}{{ - 5}}\) và \(\frac{{ - 3}}{8}\)

Ta có:

\(\begin{matrix} \dfrac{2}{{ - 5}} = \dfrac{{2.8}}{{ - 5.8}} = \dfrac{{16}}{{ - 40}} = \dfrac{{ - 16}}{{40}} \hfill \\ \dfrac{{ - 3}}{8} = \dfrac{{ - 3.5}}{{8.5}} = \dfrac{{ - 15}}{{40}} \hfill \\ \end{matrix}\)

Vì -16 < -15 => \(\frac{{ - 16}}{{40}} < \frac{{ - 15}}{{40}}\)

=> \(\frac{2}{{ - 5}} < \frac{{ - 3}}{8}\)

b) -0,85 và \(\frac{{ - 17}}{{20}}\)

Ta có:

\(- 0,85 = \frac{{ - 85}}{{100}} = \frac{{ - 85:5}}{{100:5}} = \frac{{ - 17}}{{20}}\)

=> \(- 0,85 = \frac{{ - 17}}{{20}}\)

c) \(\frac{{ - 137}}{{200}}\) và \(\frac{{37}}{{ - 25}}\)

Ta có:

\(\frac{{37}}{{ - 25}} = \frac{{37.8}}{{ - 25.8}} = \frac{{296}}{{ - 200}} = \frac{{ - 296}}{{200}}\)

Vì -137 > -296 => \(\frac{{ - 137}}{{200}} > \frac{{ - 296}}{{200}}\)

=> \(\frac{{ - 137}}{{200}} > \frac{{37}}{{ - 25}}\)

d) \(- 1\frac{3}{{10}}\) và \(- \left( {\frac{{ - 13}}{{ - 10}}} \right)\)

Ta có:

\(- 1\frac{3}{{10}} = \frac{{ - 13}}{{10}}\)

\(- \left( {\frac{{ - 13}}{{ - 10}}} \right) = - \left( {\frac{{13}}{{10}}} \right) = - \frac{{13}}{{10}}\)

=> \(- 1\frac{3}{{10}} = - \left( {\frac{{ - 13}}{{ - 10}}} \right)\)

Bài 6 trang 10 Toán 7 tập 1

So sánh các cặp số hữu tỉ sau:

Gợi ý đáp án:

a) \(\frac{{ - 2}}{3}\) và \(\frac{1}{{200}}\)

Ta có:

\(\begin{matrix} \dfrac{{ - 2}}{3} < 0;\dfrac{1}{{200}} > 0 \hfill \\ \Rightarrow \dfrac{{ - 2}}{3} < 0 < \dfrac{1}{{200}} \hfill \\ \Rightarrow \dfrac{{ - 2}}{3} < \dfrac{1}{{200}} \hfill \\ \end{matrix}\)

b) \(\frac{{139}}{{138}}\) và \(\frac{{1375}}{{1376}}\)

Ta có:

139 > 138 => \(\frac{{139}}{{138}} > 1\)

1375 < 1376 => \(\frac{{1375}}{{1376}} < 1\)

\(\begin{matrix} \Rightarrow \dfrac{{1375}}{{1376}} < 1 < \dfrac{{139}}{{138}} \hfill \\ \Rightarrow \dfrac{{1375}}{{1376}} < \dfrac{{139}}{{138}} \hfill \\ \end{matrix}\)

c) \(\frac{{ - 11}}{{33}}\) và \(\frac{{25}}{{ - 76}}\)

Ta có:

\(\begin{matrix} \dfrac{{ - 11}}{{33}} = \dfrac{{ - 11:11}}{{33:11}} = \dfrac{{ - 1}}{3} \hfill \\ \dfrac{{ - 1}}{3} = \dfrac{{ - 1.25}}{{3.25}} = \dfrac{{ - 25}}{{75}} < \dfrac{{ - 25}}{{76}} \hfill \\ \end{matrix}\)

=> \(\frac{{ - 11}}{{33}} < \frac{{25}}{{ - 76}}\)

Bài 7 trang 10 Toán 7 tập 1

Bảng dưới đây cho biết độ cao của bốn rãnh đại dương so với mực nước biển:

a) Những rãnh đại dương nào có độ cao cao hơn rãnh Puerto? Giải thích.

b) Rãnh đại dương nào có độ cao thấp nhất trong bốn rãnh trên? Giải thích.

Gợi ý đáp án:

a) Ta có: -7,7 > -8,0 > - 8,6

=> Các rãnh có độ cao hơn rãnh Puerto Rico so mới mực nước biển là: Rãnh Romanche và rãnh Peru – Chile

b) Ta có: -7,7 > -8,0 > -8,6 > -10,5

=> Rãnh Philippine có độ cao thấp nhất trong bốn rãnh đã cho.