Toán 11 Bài 13: Hai mặt phẳng song song Giải Toán 11 Kết nối tri thức trang 88, 89, 90, 91, 92, 93, 94

Giải Toán 11 Bài 13: Hai mặt phẳng song song là tài liệu vô cùng hữu ích giúp các em học sinh lớp 11 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 11 Kết nối tri thức với cuộc sống tập 1 trang 88→94.

Toán 11 Kết nối tri thức tập 1 trang 94 được biên soạn đầy đủ, chi tiết trả lời các câu hỏi từ bài 4.21 đến 4.28 giúp các bạn có thêm nhiều nguồn ôn tập đối chiếu với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết giải Toán 11 tập 1 Bài 13 Hai mặt phẳng song song Kết nối tri thức, mời các bạn cùng theo dõi tại đây.

Toán lớp 11 Kết nối tri thức tập 1 trang 94

Bài 4.21 trang 93

Trong không gian cho ba mặt phẳng phân biệt (P),(Q),(R). Những mệnh đề nào sau đây là đúng?

a) Nếu (P) chứa một đường thẳng song song với (Q)thì (P) song song với (Q)

b) Nếu (P) chứa hai đường thẳng song song với (Q) thì (P) song song với (Q).

c) Nếu (P) và (Q) song song với (R) thì (P)song song với (Q)

d) Nếu (P) và (Q)cắt (R)thì (P)và (Q) song song với nhau.

Gợi ý đáp án

a) Sai

b) Sai

c) Đúng

d) Sai

Bài 4.22 trang 94

Cho hình lăng trụ tam giác ABC⋅A′B′C′. Gọi M,N,P lần lượt là trung điểm của các cạnh AA′,BB′,CC′. Chứng minh rằng mặt phẳng (MNP) song song với mặt phẳng (ABC).

Gợi ý đáp án

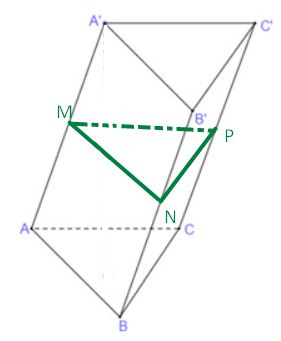
Ta có: ABB'A' là hình bình hành, M, N là trung điểm của AA', BB' nên MN // AC suy ra MN // (ABC)

Tương tự, ta có NP // BC suy ra NP (ABC)

Mặt phẳng (MNP) chứa hai đường thẳng cắt nhau MN và NP song song với mp(ABC) suy ra (MNP) //(ABC)

Bài 4.23 trang 94

Cho hình thang ABCD có hai đáy AB và CD. Qua các điểm A,D lần lượt vẽ các đường thẳng m,n song song với nhau và không nằm trong mặt phẳng (ABCD). Chứng minh rằng mp(B,m) và mp(C,n) song song với nhau.

Gợi ý đáp án

Ta có: m // n suy ra m // (C,n)

AB // CD (do ABCD là hình thang) suy ra AB // (C,n)

Mặt phẳng (B,m) chứa hia đường thẳng cắt nhau m và AB song song với mp(C,n) suy ra (B,m) // (C,n)

Bài 4.24 trang 94

Cho hình tứ diện SABC. Trên cạnh SA lấy các điểm A₁, A₂ sao cho AA₁ = A₁A₂ = A₂S Gọi (P) và (Q) là hai mặt phẳng song song với mặt phẳng (ABC) và lần lượt đi qua A₁,A₂. Mặt phẳng (P) cắt các cạnh SB, SC lần lượt tại B₁,C₁. Mặt phẳng (Q) cắt các cạnh SB, SC lần lượt tại B₂, C₂. Chứng minh BB₁ = B₁B₂ = B₂S và CC₁ = C₁C₂ = C₂S.

Gợi ý đáp án

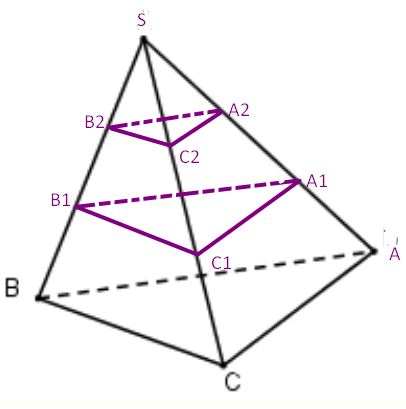
Áp dụng định lí Thales cho ba mặt phẳng (ABC), (P), (Q) và hai cát tuyến SA, SC ta có: $\frac{C_{2}S}{A_{2}S}=\frac{C_1{C}_2}{A_1{A}_2}=\frac{C{C}_1}{A{A}_1}$ mà $A{A}_1=A_1{A}_2=A_{2}S$ suy ra $C{C}_1=C_1{C}_2=C_{2}S$

Áp dụng định lí Thales cho ba mặt phẳng (ABC), (P), (Q) và hai cát tuyến SA, SB ta có: $\frac{B_{2}S}{A_{2}S}=\frac{B_1{B}_2}{A_1{A}_2}=\frac{B{B}_1}{A{A}_1}$ mà $A{A}_1=A_1{A}_2=A_{2}S$ suy ra $B{B}_1=B_1{C}_2=B_{2}S$

Bài 4.25 trang 94

Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Một mặt phẳng song song với mặt phẳng (A'B'C'D') cắt các cạnh bên của hình lăng trụ lần lượt tại A'', B", C", D". Hỏi hình tạo bởi các điểm A, B, C, D, A", B'', C'', D'' là hình gì?

Gợi ý đáp án

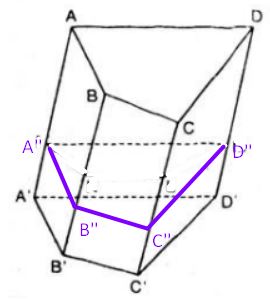
Vì các cạnh bên của hình lăng trụ ABCD.A'B'C'D' đôi một song song nên AA", BB", CC" đôi một song song.

Mặt phẳng (ABCD) song song với (A"B"C"D") (do cùng song song với (A'B'C'D')) nên ABCD.A"B"C"D" là hình lăng trụ tứ giác

Bài 4.26 trang 94

Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G và G′lần lượt là trọng tâm của hai tam giác ABC và A′B′C′

a) Chứng minh rằng tứ giác AGG‘A’ là hình bình hành.

b) Chứng minh rằng AGC.A′G′C′ là hình lăng trụ.

Gợi ý đáp án

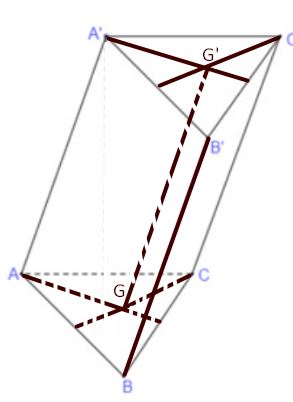
a) Ta có ABC.A'B'C' là hình lăng trụ nên ΔABC = ΔA′B′C′ suy ra AG = A'G'

Lại có (ABC) // (A'B'C'), giao tuyến của mp(AGG'A') với (ABC) và (A'B'C') lần lượt là AG, A'G' suy ra AG // A'G'

Như vậy , tứ giác AGG'A' có AG = A'G', AG // A'G' là hình bình hành

b) AGG'A' là hình bình hành suy ta AA' // GG'

Lại có AA' // CC' (do ABC.A'B'C' là hình lăng trụ)

Mặt phẳng (AGC) // (A'G'C') suy ra AGC.A'G'C' là hình lăng trụ

Bài 4.27 trang 94

Cho hình hộp ABCD.A'B'C'D'. Một mặt phẳng song song với mặt bên (ABB'A') của hình hộp và cắt các cạnh AD, BC, A'D', B'C' lần lượt tại M, N, M', N' (H.4.54). Chứng minh rằng ABNM.A'B'N'M' là hình hộp

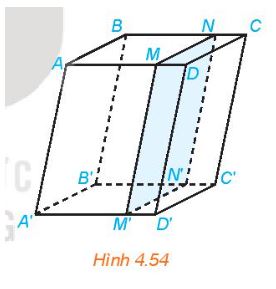
Gợi ý đáp án

Ta có (ABB'A') // (MNN'M'), (ADD′A′) ∪ (ABB′A′) = AA′,(ADD′A′) ∪ (MNN′M′) = MM′ suy ra AA'//MM'

Tương tự, BB' // NN'

ABNM.A'B'N'M' có các cạnh bên đôi một song song, (ABNM) // (A'B'N'M') suy ra ABNM.A'B'N'M' là hình lăng trụ

Ta có: (ABB'A') // (MNN'M'), (ABNM) ∪ (ABB′A′) = AB,(ABNM) ∪ (MNN′M′) = MN suy ra AB//MN

Bài 4.28 trang 94

Cầu thang xương cá là dạng cầu thang có hình dáng tương tự như những đốt xương cá, thường có những bậc cầu thang với khoảng mở lớn, tạo được sự nhẹ nhàng và thoáng đãng cho không gian sống. Trong Hình 4.55, phần mép của mỗi bậc thang nằm trên tường song song với nhau. Hãy giải thích tại sao.

Gợi ý đáp án

Các mặt của bậc thang đều song song với mặt sàn nên chúng đôi một song song với nhau

Mặt phẳng tường cắt các mặt bậc thang tại các mép nằm trên bờ tường nên chúng song song với nhau

Luyện tập Hai mặt phẳng song song