a) Đúng (theo hệ quả b).

b) Sai. Vì trong cùng một đường tròn, các góc nội tiếp cùng chắn 1 cung hoặc chắn các cung bằng nhau thì bằng nhau.

Trong một đường tròn, các góc nội tiếp bằng nhau chưa chắc cùng chắn một cung.

Vẽ hình

a) Xét đường tròn tâm B có \(\widehat {MAN}\) là góc nội tiếp chắn cung MN mà \(\widehat {MAN} = 30^\circ\)nên \(\widehat {MAN} = \dfrac{1}{2}\widehat {MBN} \\\)

\(\Rightarrow \widehat {MBN} = 2.\widehat {MAN} = 2.30^\circ = 60^\circ .\)

Suy ra \(\widehat {PBQ} = 60^\circ .\)

Lại xét đường tròn tâm C có \(\widehat {PBQ} = 60^\circ\) là góc nội tiếp chắn cung \(PQ \Rightarrow \widehat {PBQ} = \dfrac{1}{2}\widehat {PCQ} \\\)

\(\Rightarrow \widehat {PCQ} = 2.\widehat {PBQ} = 2.60^\circ = 120^\circ .\)

b) Theo chứng minh câu a) ta có \(\widehat {PCQ} = 2\widehat {PBQ} = 2.2\widehat {MAN} \\\)

\(\Leftrightarrow \widehat {PCQ} = 4.\widehat {MAN}\)

Nếu \(\widehat {PCQ} = 136^\circ \\\) 

\(\Rightarrow \widehat {MAN} = \dfrac{1}{4}\widehat {PCQ}= \dfrac{{136^\circ }}{4} = 34^\circ .\)

Áp dụng hệ quả: Góc nội tiếp chắn nửa đường tròn là góc vuông.

Cách xác định:

+ Đặt đỉnh vuông của eke trùng với một điểm N bất kỳ trên đường tròn, kẻ đường thẳng đi qua cạnh huyền của êke cắt đường tròn tại A và B ta được đường kính AB.

+ Vẫn đặt đỉnh vuông của eke tại N, xoay eke theo hướng khác, kẻ đường thẳng đi qua cạnh huyền của êke cắt đường tròn tại C và D ta được đường kính CD.

+ CD cắt AB tại tâm O của đường tròn.

Vẽ hình minh họa

Với các vị trí A, B, C trên một cung tròn thì ta được các góc nội tiếp \(\widehat{PAQ},\widehat{PBQ}, \widehat{PCQ}\) cùng chắn một cung \(\overparen{PQ}\), nên suy ra \(\widehat{PAQ} = \widehat{PBQ} = \widehat{PCQ}.\)

Vậy với các vị trí trên thì các góc sút đều bằng nhau, không có góc sút nào rộng hơn.

Vì hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) bằng nhau nên cung AB của \(\left( O \right)\) và \(\left( {O'} \right)\) bằng nhau

Suy ra \(\widehat {AMB} = \widehat {ANB}\) (các góc nội tiếp chắn các cung bằng nhau thì bằng nhau)

Do đó tam giác BMN là tam giác cân tại B.

Xét (O) có \(\widehat {AMB} = 90^\circ\)(góc nội tiếp chắn nửa đường tròn) suy ra \(AM \bot BC\)

Lại có AC là tiếp tuyến tại A nên \(\widehat {BAC} = 90^\circ\)

Xét tam giác ABC vuông tại A có AM là đường cao, theo hệ thức lượng trong tam giác vuông ta có:

\(M{A^2} = MB.MC\)(đpcm)

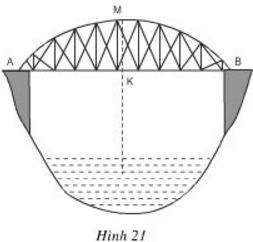
Vẽ hình minh họa:

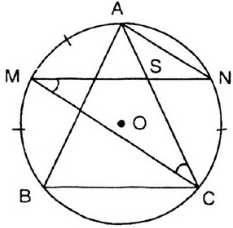
+) Chứng minh SM = SC

\(\widehat {{M_1}} = \widehat {{C_2}}\) (2 góc ở vị trí so le trong)

\(\widehat{{{C}_{1}}}=\widehat{{{C}_{2}}}\) (2 góc nội tiếp chắn 2 cung bằng nhau 

Nên suy ra \(\widehat{{{M}_{1}}}=\widehat{{{C}_{1}}}\)

Suy ra tam giác SMC là tam giác cân tại S. Vậy SM = SC.

+) Chứng minh SA = SN

Ta có: \(\widehat {{M_1}} = \widehat {{A_1}}\)( 2 góc nội tiếp cùng chắn cung NC)

\(\widehat {{C_1}} = \widehat {{N_1}}\)(2 góc nội tiếp cùng chắn cung AM)

Mà \(\widehat{{{M}_{1}}}=\widehat{{{C}_{1}}}\) (chứng minh trên)

\(\widehat{{{A}_{1}}}=\widehat{{{N}_{1}}}\) (vì cùng bằng 2 góc bằng nhau)

Vậy tam giác SAN cân tại S. Nên SA = SN (đpcm)